Numer lub liczba Eulera E ile jest warte, właściwości, aplikacje

On Numer lub liczba Eulera E Jest to dobrze znana stała matematyczna, która pojawia się często w wielu zastosowaniach naukowych i ekonomicznych, wraz z liczbą π i innymi ważnymi liczbami w matematyce.

Kalkulator naukowy rzuca następującą wartość dla liczby E:

Rysunek 1. Liczba Eulera często pojawia się w nauce. Źródło: f. Zapata.

E = 2.718281828…

Ale na przykład znanych jest wiele innych dziesiętnych:

E = 2.71828182845904523536…

A współczesne komputery pozwoliły na bilion dziesiętne do liczby E.

To jest liczba irracjonalny, co oznacza, że ​​ma nieskończoną liczbę dziesiętnych bez powtarzalnego wzorca (sekwencja 1828 pojawia się dwa razy na początku i nie powtarza się).

I oznacza to również, że liczby E nie można uzyskać jako ilorazu dwóch liczb całkowitych.

[TOC]

Historia

Numer I Został zidentyfikowany przez naukowca Jacquesa Bernoulli w 1683 r., Kiedy badał problem złożonego zainteresowania, ale wcześniej pośrednio pojawił się w pracach szkockiego matematyka Johna Napiera, który wynalazł logarytmy na 1618.

Jednak to Leonhard Euler w 1727. Dlatego jest również znany jako Numer Eulera a także jako naturalna podstawa dla logarytmów neperiańskich (wykładnik).

Ile jest warta liczba e?

Liczba e vale:

E = 2.71828182845904523536…

Punkty zawiesinowe oznaczają, że istnieje nieskończona liczba dziesiętnych, a w rzeczywistości miliony z nich są znane z obecnych komputerów.

Reprezentacje liczby E

Istnieje kilka sposobów zdefiniowania e, które opisujemy poniżej:

Liczba e jako limit

Jednym z różnych sposobów wyrażania liczby E jest ten, który naukowca Bernoulli znalazł w swojej pracy nad zainteresowaniem złożonym:

W którym musisz wykonać wartość N Bardzo duża liczba.

Łatwo jest sprawdzić, za pomocą kalkulatora, że ​​kiedy N Jest bardzo duży, poprzednie wyrażenie ma tendencję do wartości I Podane powyżej.

Może ci służyć: funkcja bijkłowców: co to jest, jak to się dzieje, przykłady, ćwiczenia

Oczywiście możemy zadać sobie pytanie, jak duże można to zrobić N, Dlatego próbujemy z okrągłymi liczbami, na przykład:

n = 1000; 10.000 lub 100.000

W pierwszym przypadku otrzymujesz e = 2.7169239… . W drugim e = 2.7181459… a na trzecim jest znacznie bardziej bliski wartości I: 2.7182682. Możemy już to wyglądać z n = 1.000.000 lub większe, podejście będzie jeszcze lepsze.

W języku matematycznym procedura tworzenia N Zbliża się do bardzo dużej wartości, nazywa się limit do nieskończoności I jest tak oznaczone:

Aby oznaczyć nieskończoność, używany jest symbol „∞”.

Liczba e jako suma

Możliwe jest również zdefiniowanie liczby E poprzez tę operację:

Liczby, które pojawiają się w mianowniku: 1, 2, 6, 24, 120 ... odpowiadają operacji N!, Gdzie:

N! = n. (N-1).(N-2). (N-3) ..

I z definicji 0! = 1.

Łatwo jest sprawdzić, czy im więcej dodatków jest dodawane, tym większa jest osiągana liczba I.

Wykonajmy kilka testów z kalkulatorem, dodając coraz bardziej dodatki:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Im więcej terminów są dodawane do suma, tym bardziej wynik jest podobny I.

Matematycy opracowali zwartą notację dla tych kwot, które obejmują wiele terminów, używając symbolu sumowego σ:

To wyrażenie jest odczytywane jako „suma n = 0 do nieskończoności 1 między N czynnik”.

Liczba e z geometrycznego punktu widzenia

Liczba E ma reprezentację graficzną związaną z obszarem pod wykresem krzywej:

y = 1/x

Gdy wartości x wynoszą od 1 do E, obszar ten jest wart 1, jak pokazano na poniższym rysunku:

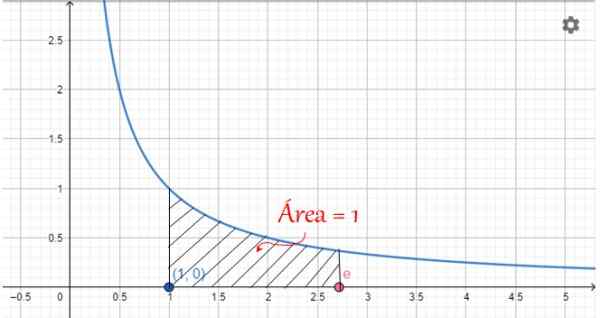Rysunek 2. Graficzna reprezentacja liczby E: Obszar pod krzywą 1/x, między x = 1 a x = e o'clock. Źródło: f. Zapata.

Liczba właściwości E

Niektóre właściwości liczby E to:

Może ci służyć: Funkcja rosnąca: jak to zidentyfikować, przykłady, ćwiczenia

-Innymi słowy, jest to irracjonalne, nie można go uzyskać po prostu poprzez dzielenie dwóch liczb całkowych.

-Numer I To także Liczba transcendentna, co oznacza że I Nie jest to rozwiązanie żadnego równania wielomianowego.

-Jest to związane z czterema innymi słynnymi liczbami w dziedzinie matematyki, a mianowicie: π, i, 1 i 0, poprzez tożsamość Eulera:

I^πi + 1 = 0

-Połączenia Liczby zespolone można wyrazić przez E.

-Stanowi dziś podstawy logarytmów naturalnych lub neperiańskich (oryginalna definicja Johna Napiera nieco różni się).

-Jest to jedyna liczba taka, że ​​jego neperiański logarytm jest wart 1, to znaczy:

 LN E = 1

Aplikacje

Statystyka

Liczba E pojawia się bardzo często w dziedzinie prawdopodobieństwa i statystyki, pojawiając się w różnych rozkładach, takich jak normalny lub gaussowski, poisson i innych.

Inżynieria

W inżynierii jest częste, ponieważ funkcja wykładnicza y = e^X Jest obecny na przykład w mechanice i elektromagnetyzmie. Wśród wielu aplikacji możemy zacytować:

-Kabel lub łańcuch, który wisi podlegający końcom, przyjmuje kształt krzywej podanej przez:

y = (e^X + I^-X) /2

-Kondensator C początkowo rozładowywany, który łączy się szeregowo z rezystancją R i źródłem napięcia V do załadowania, nabywa określone obciążenie Q w zależności od czasu t podanego przez:

Q (t) = CV (1-E^-T/rc)

biologia

Funkcja wykładnicza y = a.I^Bx, Ze stałą A i B jest stosowany do modelowania wzrostu komórek i wzrostu bakterii.

Fizyczny

W fizyce jądrowej rozkład radioaktywny i oznaczanie wieków są modelowane przez radiowęglowe datowane.

Gospodarka

W obliczeniach złożonych zainteresowań liczba E pojawia się naturalnie.

Załóżmy, że masz pewną kwotę pieniędzy P_albo, zainwestować go w rocznej stopie procentowej.

Jeśli pieniądze zostaną na 1 rok, po tym czasie będziesz miał:

P (1 rok) = P_albo + P_albo.i = p_albo (1+ i)

Po kolejnym roku bez dotykania go będziesz mieć:

Może ci służyć: teoretyczne prawdopodobieństwo: jak to wyciągnąć, przykłady, ćwiczenia

P (2 lata) = P_albo + P_albo.i + (p_albo + P_albo .i) i = p_albo +2 p_albo.I + p_albo.Siema²  = PO (1+i)²

I w ten sposób N lata:

P = p_albo (1+i)^N

Teraz pamiętaj o jednej z definicji E:

Wygląda trochę jak wyrażenie P, więc musi istnieć związek.

Dystrybuujemy nominalną stopę procentową Siema W N Okresy, w ten sposób złożona stopa procentowa będzie I/N:

P = p_albo [1+ (I/N)]^N

To wyrażenie wygląda nieco bardziej na nasz limit, ale nie jest jeszcze dokładnie takie samo.

Jednak po niektórych manipulacjach algebraicznych można wykazać, że dokonanie tej zmiany zmiennej:

h = n/i → i = n/h

Nasze pieniądze p stają się:

P = p_albo [1+ (1/h)]^Cześć = P_albo [1+ (1/h)]^HSiema

A co jest wśród kluczy, nawet jeśli jest napisane z listem H, Jest równy argumentowi limitu, który określa liczbę e, brakuje tylko limitu.

Zróbmy  H → ∞, a to, co jest między klawiszami, jest przekształcane w liczbę I. Nie oznacza to, że musimy czekać nieskończenie wielki czas, aby wypłacić nasze pieniądze.

Jeśli wyglądamy dobrze, robiąc to H = n/i I dążąc do ∞, tak naprawdę zrobiliśmy, aby rozdzielić stopę procentową w bardzo, bardzo małych okresach: bardzo małe:

I = n/h

To się nazywa Ciągła kapitalizacja. W takim przypadku kwota pieniędzy można łatwo obliczyć w następujący sposób:

P = p_albo .I^Siema

Gdzie jestem roczną stopą procentową. Na przykład poprzez zdeponowanie od 12 do 9 % rocznie, poprzez ciągłą kapitalizację, po roku masz:

P = 12 x e^{0.09 × 1} € = 13.13 €

Z zyskiem 1.13 €.

Bibliografia

1. Ciesz się matematyką. Złożone odsetki: skład okresowy. Odzyskane z: FaveMatimaticas.com.
2. Figuera, J. 2000. Matematyka 1st. Urozmaicony. Edycje CO-Bo.
3. Garcia, m. Liczba E w obliczeniach elementarnych. Odzyskane z: matematyki.Ciens.UCV.Iść.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Larson, r. 2010. Obliczanie zmiennej. 9na. Wydanie. McGraw Hill.