Dodatkowe kąty, które są obliczeniami, przykładami, ćwiczeniami

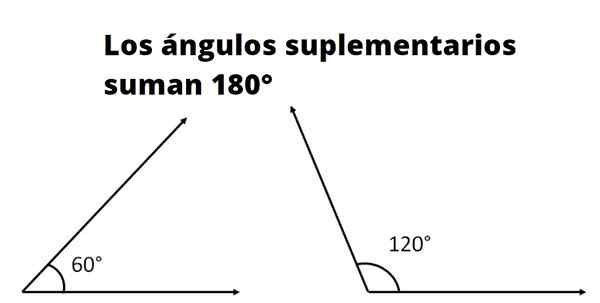
Dwa lub więcej to Dodatkowe kąty Jeśli suma jego miar odpowiada miarę płaskiego kąta. Miara płaskiego kąta, zwanego również płaskim kątem, w stopniach wynosi 180º, a w radiach wynosi π.

Na przykład stwierdzamy, że trzy kątowe kątowe trójkąta są uzupełniające, ponieważ suma jego miar wynosi 180º. Trzy kąty pokazano na rycinie 1. Z powyższego wynika, że ​​α i β są uzupełniające, ponieważ są sąsiadujące, a ich pełna suma płaskiego kąta.

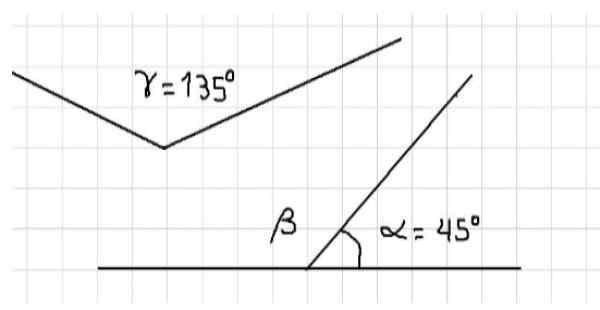
Rycina 1: α i β są uzupełniające. α i γ są uzupełniające. Źródło: f. Zapata.

Również na tej samej figurze istnieją kąty α i γ, które są również uzupełniające, ponieważ suma ich miar jest równa stopniu płaskiego kąta, to znaczy 180º. Nie można powiedzieć, że kąty β i γ są uzupełniające, ponieważ zarówno pod kątem rozwartych, ich miary są większe niż 90º.

Źródło: Lafer.com

Z drugiej strony można powiedzieć, że miara kąta β jest równa miary kąta γ, ponieważ jeśli β jest uzupełniający α i γ, uzupełnia α, to β = γ = 135º.

[TOC]

Przykłady

W poniższych przykładach należy znaleźć nieznane kąty, wskazane z przesłuchaniem na rycinie 2. Obejmują one od najprostszych przykładów po nieco bardziej skomplikowane niż czytelnik powinien być bardziej ostrożny.

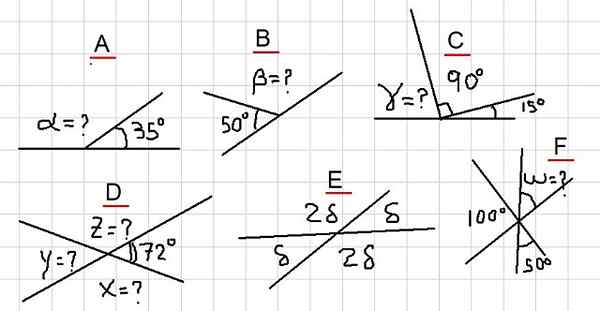Rysunek 2. Różne przykłady kątów uzupełniających. Źródło: f. Zapata.

Przykład a

Na rysunku mamy, że sąsiednie kąty α i 35º, dodają płaski kąt. To znaczy, α + 35º = 180º i dlatego się spełnia, że: α = 180º- 35º = 145º.

Przykład b

Ponieważ β jest uzupełniający kąt 50º, następuje, że β = 180º - 50º = 130º.

Może ci służyć: jakie są elementy przypowieści? (Części)

Przykład c

Z ryc. 2c zauważono następującą sumę: γ + 90º + 15º = 180º. To znaczy γ jest uzupełniający z kątem 105º = 90º + 15º. Stwierdzono zatem, że: 

γ = 180º- 105º = 75º

Przykład d

Ponieważ X jest uzupełniający z 72º, wynika z tego, że x = 180º - 72º = 108º. Ponadto i jest uzupełniający z x, a następnie y = 180º - 108º = 72º.

I wreszcie Z jest uzupełniający z 72º, a zatem z = 180º - 72º = 108º.

Przykład e

Kąty δ i 2δ są uzupełniające, a zatem δ + 2δ = 180º. Co oznacza, że ​​3Δ = 180º, a to z kolei pozwala na pisanie: δ = 180º / 3 = 60º.

Przykład f

Jeśli nazwiemy kąt między 100º a 50º, należy je uzupełnić, ponieważ zaobserwowano, że ich pełna suma płaskiego.

Wynika z tego, że u = 150º. Ponieważ u wierzchołek do W, wówczas w = u = 150º.

Ćwiczenia

Trzy ćwiczenia są proponowane poniżej, we wszystkich z nich wartość kątów A i B należy znaleźć w stopniach, tak aby relacje pokazane na rycinie 3 zostały spełnione. Pojęcie kątów uzupełniających jest wykorzystywane w rozdzielczości wszystkich z nich.

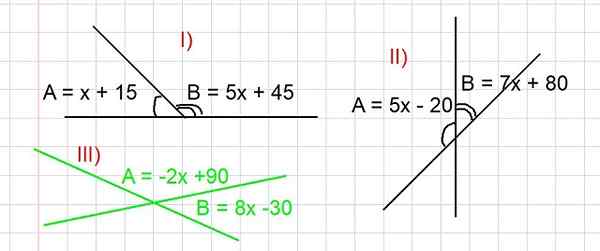Rysunek 3. Liczba rozwiązania ćwiczeń I, II i III na temat dodatkowych kątów. Wszystkie kąty są wyrażane w stopniach. Źródło: f. Zapata.

- Ćwiczenie I

Określ wartości kątów A i B części I) na rycinie 3.

Rozwiązanie

A i B są uzupełniające, gdzie należy wymienić A + B = 180 stopni, a następnie ekspresja A i B jest zastąpiona jako funkcja x, jak pojawia się na obrazie:

(x + 15) + (5x + 45) = 180

Uzyskuje się równanie liniowe pierwszego rzędu. Aby go rozwiązać, warunki są wyrzucane: Warunki:

6 x + 60 = 180

Może ci służyć: liczby rzeczywiste: historia, przykłady, nieruchomości, operacje

Dzielenie obu członków między 6 to:

x + 10 = 30

I wreszcie wyczyszczenie, wynika z tego, że x jest warte 20º.

Teraz wartość x należy wymienić, aby znaleźć uporządkowane kąty. Stamtąd musisz podać A to: a = 20 +15 = 35º.

A ze swojej części kąt B wynosi B = 5*20 + 45 = 145º.

- Ćwiczenie II

Znajdź wartości kątów A i B części II) na rycinie 3.

Rozwiązanie

Ponieważ A i B są kątami uzupełniającymi, a + B = 180 stopni ma. Zastąpienie wyrażenia A i B jako funkcji x podanej w części II) na rycinie 3 to:

(-2x + 90) + (8x - 30) = 180

Ponownie uzyskuje się równanie pierwszego stopnia, dla którego warunki muszą być dogodnie grupa:

6 x + 60 = 180

Dzielenie obu członków między 6 to:

x + 10 = 30

Gdzie następuje, że x jest warte 20º.

To znaczy, że kąt a = -2*20 + 90 = 50 °. Podczas gdy kąt B = 8*20-30 = 130.

- Ćwiczenie III

Określ wartości kątów A i B części III) na rycinie 3 (w kolorze zielonym).

Rozwiązanie

Ponieważ A i B są kątami uzupełniającymi, a + B = 180 stopni ma. Wyrażenie A i B należy wymienić jako funkcję x podaną na rycinie 3, którą masz:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Dzielenie obu członków przez 12, aby wyczyścić wartość x, masz:

x + 5 = 15

Wreszcie okazuje się, że x jest warte 10 stopni.

Teraz zamień, aby znaleźć kąt A: A = 5*10-20 = 30 °. A dla kąt B: B = 7*10 + 80 = 150º

Może ci służyć: jaki jest zakres statystyk? (Z przykładami)

Dodatkowe kąty w dwóch podobieństwach wycięte przez siekrę

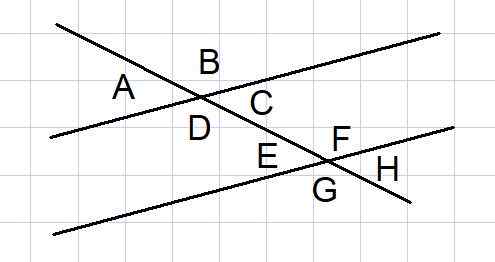Rysunek 4. Kąty między dwoma podobieństwami wyciętymi przez sekundę. Źródło: f. Zapata.

Dwie równoległe linie wycięte przez siekant to zwykła konstrukcja geometryczna w niektórych problemach. Wśród takich linii powstaje 8 kąty, jak pokazano na rycinie 4.

Z tych 8 kątów niektóre pary kątów są uzupełniające, które wymieniamy poniżej:

1. Zewnętrzne kąty do i b, a zewnętrzne g i h
2. Kąty wnętrza D i C, a wnętrza e i f
3. Kąty zewnętrzne A i G, a zewnętrzne B i H
4. Kąty wewnętrzne d i e, a więźniowie c i f

Zgodnie z kompletnością nazywane są również równe kąty:

1. Wewnętrzne naprzemienne: D = F i C = E
2. Zewnętrzne naprzemienne: a = h i b = g
3. Odpowiednie: a = e i c = h
4. Przeciwieństwa według Vertex A = C i E = H
5. Odpowiednie: B = F i D = G
6. Przeciwieństwa według Vertex B = D i F = G

- Ćwiczenie IV

W odniesieniu do ryc. 4, w którym kąty pokazują między dwiema równolegle wyciętych przez siekant, określ wartość wszystkich kąta w radianach, wiedząc, że kąt a = π/6 Radian.

Rozwiązanie

A i B są dodatkowymi kątami zewnętrznymi Dlatego b = π - a = π - π/6 = 5π/6

A = e = c = h = π/6

B = f = d = g = 5π/6

Bibliografia

1. Baldor, J. DO. 1973.Płaska i przestrzeń geometria. Cultural American Cultural. 
2. Prawa i formuły matematyczne. Systemy pomiaru kąta. Pobrano z: Ingemecanica.com.
3. Wentworth, G. Geometria planety. Odzyskane z: Gutenberg.org.
4. Wikipedia. Dodatkowe kąty. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Przenośnik. Odzyskane z: jest.Wikipedia.com
6. Zapata f. Goniometr: historia, części, operacja. Pobrano z: Lifer.com