Zarejestrowany kąt definicji koła, twierdzenia, przykłady

On Zarejestrowany kąt koła Jest to ten, który ma swój wierzchołek na obwodzie, a jego półstaight są suche lub styczne do tego samego. W rezultacie zarejestrowany kąt będzie zawsze wypukły lub płaski.

Na rycinie 1 reprezentowano kilka kąty zarejestrowanych w ich odpowiednich obwodach. Kąt ∠EDF jest zarejestrowany przez posiadanie jego wierzchołka D na obwodzie i dwóch półnośnikach [z) i [df) suszenia obwodu. 

Rysunek 1. Kilka wpisanych kątów na temat ich odpowiednich obwodów. Źródło: f. Zapata z Geogebra.

Podobnie kąt ∠HGI jest zarejestrowany, ponieważ ma jego wierzchołek w obwodzie i suche strony do tego samego.

Kąty ∠KJR i ∠UST są również rejestrowane z obwodem. Pierwszy ma jedną stronę sekunda, a druga styczna, podczas gdy druga ma swoje dwie strony styczne do obwodu, tworząc płaski kąt płaszczyzny (180º).

Niektórzy autorzy nazywają póła inkomplikowanym kątem do tego, który ma jedną ze swoich stron styczną do obwodu, ale w tym artykule jest uważany za zarejestrowany.

Wszelkie zarejestrowane kąt określa lub subteluje łuk powiązany z tym samym. Na przykład na rysunku 2 zarejestrowany kąt ∠ABC subteluje łuk a⌒c długości d.

Ta sama rysunek pokazuje kąt ∠DOE, który nie jest zarejestrowany w obwodzie, ponieważ nie ma jego wierzchołka na obwodzie, ale w środku lub.

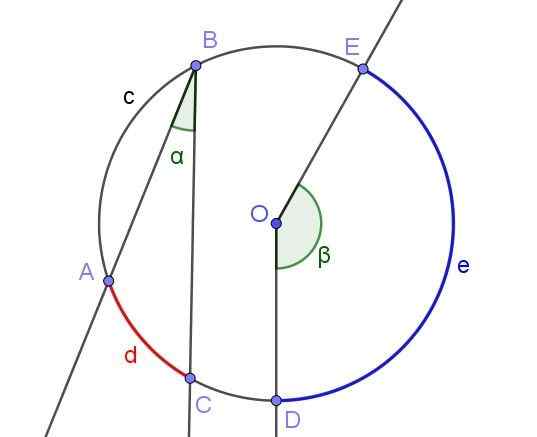Rysunek 2. Zarejestrowany kąt ∠ABC i kąt centralny ∠DOE. Źródło: f. Zapata z Geogebra.

[TOC]

Kąt centralny

Oprócz zarejestrowanego kąta, Kąt centralny, który jest tym, którego wierzchołek znajduje się w środku obwodu i którego boki przecinają obwód.

Może ci służyć: różnica między wspólną frakcją a liczbą dziesiętną

Miara promieniowego kąta centralnego jest ilorazem między łukiem, który subtacjonuje, to znaczy łukiem obwodu między bokami kąta i promieniem obwodu.

Jeśli obwód jest jednolity (promień 1), wówczas długość łuku w tych samych jednostkach radiowych jest miarą kąta w radiach.

A gdy miara kąta jest wymagana w stopniach, miara jest mnożona w radianach przez współczynnik 180º/π.

Instrumenty pomiarowe kątów zawsze używają kąta centralnego i długości łuku, który został subtelny przez ten bezpośrednio skalibrowany w stopniach. Oznacza to, że za każdym razem, gdy mierzony jest kąt, w tle mierzona jest długość łuku substancji substancji pod kątem środkowym.

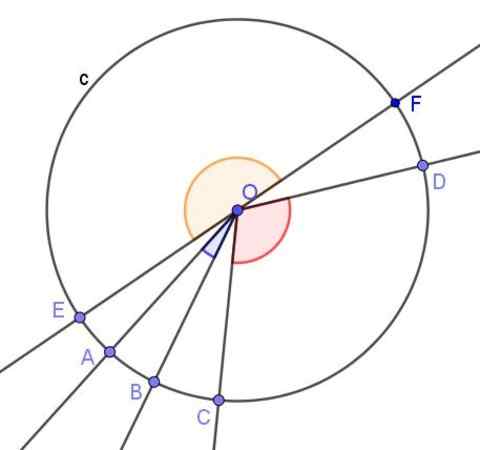Rysunek 3. Kilka centralnych kątów obwodu. Źródło: f. Zapata z Geogebra.

Twierdzenia

- Twierdzenie 1 (zarejestrowany kąt i kąt centralny)

Miara zarejestrowanego kąta jest połowa miary kąta środkowego, jeśli oba kąty subtytują ten sam łuk.

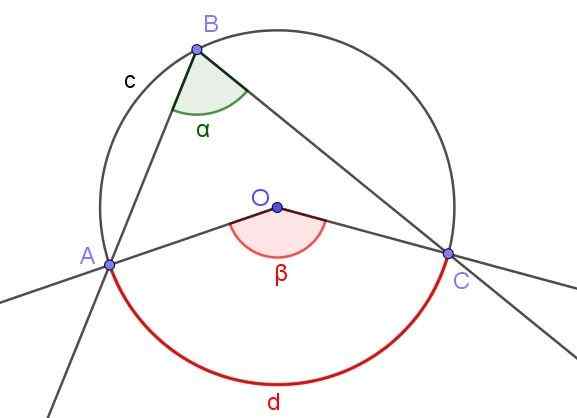Rysunek 4. Zarejestrowany kąt ∠ABC i kąt centralny ∠AOC, który podzielony na ten sam łuk A⌒c. Źródło: f. Zapata z Geogebra.

Rycina 4 pokazuje dwa kąty ∠ABC i ∠AOC, które przecinają ten sam łuk obwodu A⌒c.

Jeżeli miara zarejestrowanego kąta jest α, wówczas miara β kąta centralnego jest dwukrotnie większą niż miara zarejestrowanego kąta (β = 2 α), ponieważ oba odejmują ten sam zmierzony łuk D.

Demonstracja 1

Aby zademonstrować twierdzenie 1, rozpocznie się kilka konkretnych przypadków, aż do osiągnięcia ogólnego przypadku.

Może ci służyć: Law Sandwich: Wyjaśnienie i ćwiczenia

Załóżmy, że zarejestrowany kąt, w którym jedna z jego stron przechodzi przez środek obwodu, jak pokazano na rycinie 5.

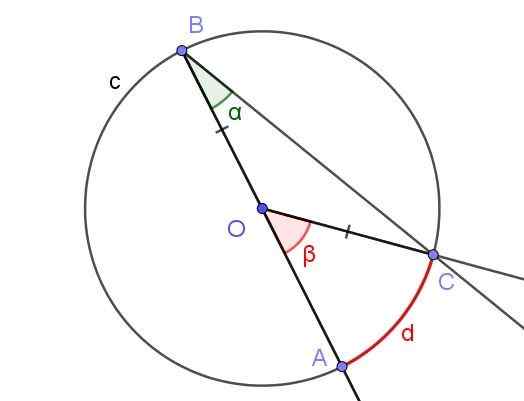Rysunek 5. Zarejestrowany kąt ∠ABC z bokiem [BA) przez O i kąt centralny ∠AOC. Źródło: f. Zapata z Geogebra.

W tym przypadku powstaje trójkąt Isosceles COB, ponieważ [OC] = [OB].

W trójkącie Isosceles kąty przylegające do podstawy są takie same, dlatego muszą one ci. Z drugiej strony ∠COB = 180º - β.

Biorąc pod uwagę sumę wewnętrznych kątów trójkąta COB:

α + α + (180º - β) = 180º

Gdzie następuje, że 2 α = β lub co jest równoważne: α = β/2. Zbiega się to z tym, co twierdzi Twierdzenie 1: miara zarejestrowanego kąta jest połowa kąta środkowego, jeśli oba kąty złożą tę samą linę [AC].

Demonstracja 1b

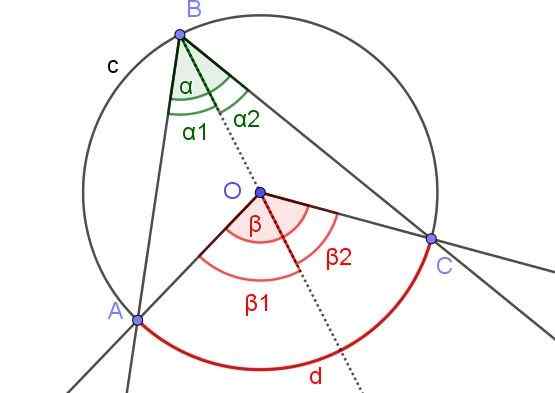Rysunek 6. Konstrukcja pomocnicza w celu wykazania, że ​​α = β/2. Źródło: f. Zapata z Geogebra.

W takim przypadku występuje wpisany kąt ∠ABC, w którym środek lub obwód znajduje się wewnątrz kąta.

Aby zademonstrować Twierdzenie 1 W tym przypadku narysowany jest pół -prawidłowy pomocnik [BO), tak że istnieją dwa zarejestrowane kąty ∠ABO i ∠OBC sąsiadowane ze wspomnianym półreakalnym.

Podobnie mają one kąty centralne β₁ i β₂ w sąsiedztwie wspomnianego pół -orzeka. W ten sposób masz taką samą sytuację jak w demonstracji 1, więc można stwierdzić, że α₂ = β₂ /2 i α₁ = β₁ /2. Jak α = α₁ + α₂ i β = β₁ + β₂ Istnieje zatem, że α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Może ci służyć: rodzaje całek

Podsumowując α = β / 2, który spełnia twierdzenie 1.

- Twierdzenie 2

Jeśli dwa lub więcej zarejestrowanych kątów podsumowały ten sam łuk, mają one tę samą miarę.

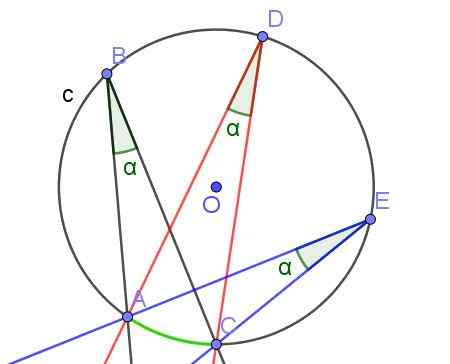Rysunek 7. Zarejestrowane kąty o równej miarę α, ponieważ subteksują one ten sam łuk A⌒c. Źródło: f. Zapata z Geogebra.

- Twierdzenie 3

Zarejestrowane kąty podtytują ciągi tej samej miary są takie same.

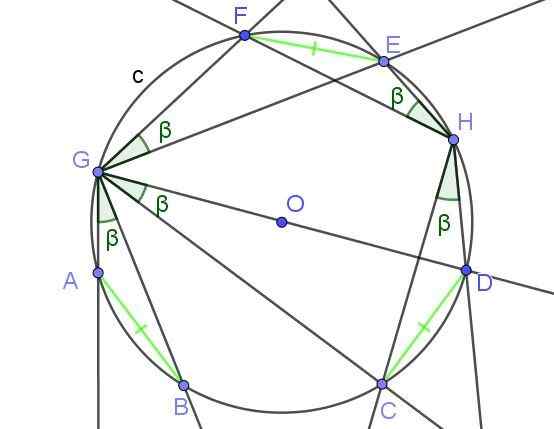Cyfra 8. Wpisane kątki, które subtude liny o równej mierze, mają równą miarę β. Źródło: f. Zapata z Geogebra.

Przykłady

- Przykład 1

Wykazać, że zapisany kąt składa średnica jest kątem prostym.

Rozwiązanie

Centralny kąt ∠AOB związany z średnicą jest płaski kąt, którego miara wynosi 180º.

Zgodnie z Twierdzeniem 1, każdy kąt zarejestrowany w obwodzie, który upada ta sama lina (w tym przypadku średnicy), ma jako zmierzenie połowy kąta środkowego, który subtypuje tę samą linę, która dla naszego przykładu to 180º/2 = 90º.

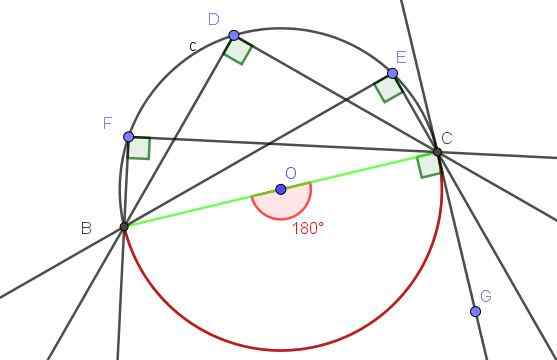Rysunek 9. Wszelkie zarejestrowane kąt, który upływa do średnicy, jest kątem prostym. Źródło: f. Zapata z Geogebra.

- Przykład 2

Linia (BC) styczna w a a do obwodu c, określa wpisany kąt ∠BAC (patrz ryc. 10).

Sprawdź, czy twierdzenie 1 zarejestrowanych kątów jest spełnione.

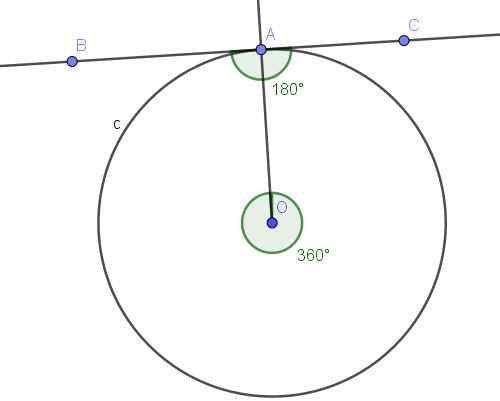Rysunek 10. Zarejestrowany kąt BAC i jego wypukły kąt centralny AOA. Źródło: f. Zapata z Geogebra.

Rozwiązanie

Kąt ∠BAC jest zarejestrowany, ponieważ jego wierzchołek jest na obwodzie, a jego boki [AB) i [AC) są styczne do obwodu, więc definicja zapisanego kąta jest spełniona.

Z drugiej strony, wpisany kąt ∠BAC subteluje łuk A⌒A, który jest pełnym obwodem. Centralny kąt, który subteluje łuk A⌒A, jest kątem wypukłym, którego miara jest pełny kąt (360º).

Zarejestrowany kąt podtytuje pełny łuk mierzy połowę powiązanego kąta centralnego, to znaczy ∠BAC = 360º/2 = 180º.

Ze wszystkich powyższych udowodniono, że ten konkretny przypadek spełnia twierdzenie 1.

Bibliografia

1. Baldor. (1973). Geometria i trygonometria. Redakcja kulturalna Ameryki Środkowej.
2. I. DO. (2003). Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
3. Geometria 1st. Kąty w obwodzie. Odzyskane z: edu.Xunta.Jest/
4. Cała nauka. Proponowane ćwiczenia kątów w obwodzie. Odzyskane z: Francessphysics.Blogspot.com
5. Wikipedia. Zarejestrowany kąt. Odzyskane z: jest.Wikipedia.com