Mnożenie ułamków, jak się to robi, przykłady, ćwiczenia

Mnożenie ułamków Jest to operacja arytmetyczna między dwoma lub więcej frakcjami, która powoduje powstanie nowej frakcji. Jego licznik mnoży liczniki uczestniczących frakcji, a mianownik jest w ten sam sposób.

Zobaczmy to z przykładem na poniższym obrazku. Załóżmy, że istnieją dwie frakcje A/B i C/D, z B i D różniące się od 0.

Rysunek 1. Mnożenie ułamków to operacja przeprowadzona online. Źródło: f. Zapata.

Aby przeprowadzić mnożenie między nimi, produkt jest wytwarzany między licznikami a także produktem mianowników. W ten sposób powstaje nowa frakcja, w której licznik i mianownik są odpowiednio: (A × C) i (B × D).

Ta procedura jest łatwo rozszerzona na mnożenie trzech i większej liczby frakcji. Zobaczmy więcej szczegółów poniżej.

W jaki sposób dokonuje się pomnożenia ułamków?

Produkt można symbolizować za pomocą krzyża lub punktu przeplatanego między ułamkami. Ponadto należy wziąć pod uwagę, że ułamki mogą mieć znak pozytywny lub znak ujemny, dlatego należy zachować ostrożność przestrzegania zasady znaków:

-Gdy dwie liczby równych znaków są pomnożone, produkt jest dodatni.

-Jeśli dwie ilości różnych znaków są pomnożone, wynik jest ujemny.

Tą drogą:

Po przeprowadzeniu procedury ułamek jest uproszczony, jeśli to możliwe. To w przypadku, gdy licznik i mianownik nie są ze sobą kuzynami. Na przykład:

Jeśli licznik i mianownik uczestniczących frakcji nie są ze sobą kuzynami, wygodne jest uproszczenie ich przed pomnożeniem frakcji. W ten sposób przy uruchomieniu produktów uzyskuje się mniejsze i łatwiejsze do zarządzania liczby.

Może ci służyć: ile rozwiązań ma równanie kwadratowe?

Właściwości mnożenia frakcji

Produkt o 0

Każda frakcja pomnożona przez 0 jest równa 0:

Produkt po 1

Każda frakcja pomnożona przez 1 jest równa sobie:

Dlatego 1 jest brany pod uwagę Element neutralny mnożenia. Zauważ, że cała liczba 1 ma ułamkowe wyrażenie:

W taki sposób, że możemy pomnożyć do 1 przez dowolną frakcję, za pomocą już wyjaśnionej zasady. Więc:

Własność przemienna

Mnożenie ułamków jest przemienne, co oznacza, że ​​kolejność czynników nie zmienia produktu:

Łączność

Mnożenie ułamków jest również asocjacyjne, możemy zweryfikować poprzez pomnożenie trzech frakcji:

Gdzie, jak zawsze, mianowniki B, D i F różnią się od 0.

Słowami: jeśli zamierzamy pomnożyć trzy frakcje, możemy wybrać produkt pierwszych dwóch i pomnożyć wynik przez trzecią frakcję. Lub pomnóż ostatnie dwa i ich wynik w końcu pomnoż go przez pierwszy z ułamków.

Bez względu na wybraną kolejność, wynik będzie taki sam. Sprawdźmy to:

Aby wykonać operację, dwie pierwsze frakcje zostały pomnożone od lewej do prawej. Wynik został z kolei pomnożony przez trzecią część, aby uzyskać wynik końcowy.

Drugą alternatywą jest pomnożenie dwóch ostatnich frakcji, pozostawiając pierwsze oczekiwanie. Czytelnik widzi, że wynik pośredni składa się z dwóch różnych frakcji od tych uzyskanych w drugiej stronie. Ale końcowy wynik jest taki sam:

Własność dystrybucyjna dotycząca sumy

Niech trzy frakcje A/B, C/D i E/F, z B, D i F różni się od 0. Mnożenie jest dystrybucyjne w odniesieniu do sumy.

Załóżmy, że chcemy wykonać następującą operację:

Sposób, w jaki wycofuje się, przez tę nieruchomość, jest następujący:

Może ci służyć: Turs Tukey: Co to jest w przypadku przykładu rozwiązanego ćwiczenia

Dlatego iloczyn liczby dla suma dwóch innych można wykonać, dodając dwa produkty: pierwszy dla drugiego i pierwszego przez trzeci. Przykład jest bardzo prosty:

Wynik końcowy wydaje się uprościł do maksimum, jak wyjaśniono powyżej.

Przykłady

Mnożenie frakcji przez liczbę całkowitą

Załóżmy, że chcesz pomnożyć frakcję A/B przez całkowitą liczbę całkowitą n:

Wcześniej widzieliśmy, że numer 1 można wyrazić jako ułamek, po prostu umieszczając jako mianownik na 1. Możemy zrobić to samo z każdą liczbą całkowitą n, ponieważ podzielenie go przez 1 wcale tego nie zmienia. Więc:

Na przykład:

Przykład 2: Mnożenie frakcji przez liczbę mieszaną

Mieszana liczba lub frakcja mieszana, to ta, która ma całą część i część ułamkową. Aby wykonać produkt takiej liczby, albo z ułamkiem, kolejną liczbą mieszaną lub z liczbą całkowitą, konieczne jest przekształcenie go z kolei w ułamek.

Ułamek reprezentujący liczbę mieszaną jest Ułamek niewłaściwy, a, którego licznik ma większą wartość bezwzględną niż mianownik.

Możemy go uzyskać poprzez sumę całej części, wygodnie wyrażona jako frakcja, umieszczając 1 jako mianownik, a także część ułamkową.

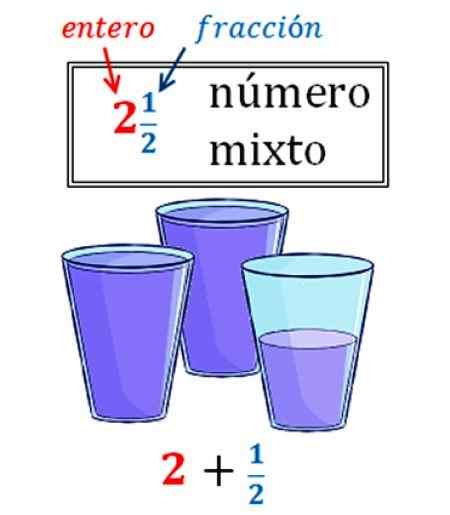Rysunek 2. Mieszana liczba przekształcona w ułamek. Źródło: Wikimedia Commons.

Na obrazie istnieje przykład liczby mieszanej, który pokazuje, jak często. Mamy 2 i pół szklanki wody, które jako liczba mieszana jest wyrażana w ten sposób:

2 ½

Otrzymujemy niewłaściwy ułamek, który go reprezentuje:

Załóżmy teraz, że chcemy znaleźć 3/4 części dwóch i pół szklanek wody. To, co musimy zrobić, to pomnożyć 3/4 przez uzyskaną niewłaściwą frakcję:

Może ci służyć: rozkład Poissona: wzory, równania, model, właściwości

Rozwiązane ćwiczenia

Ćwiczenie 1

Wykonaj następującą operację:

Rozwiązanie

Liczba 1 ¾ jest liczbą mieszaną. Cała jego część to 1, a część ułamkowa wynosi ¾. Jeśli wykonamy operację: 1 + ¾, liczba mieszana jest przekształcana w niewłaściwą frakcję.

1 + ¾ = (4 + 3) /4 = 7/4

Po przekształceniu mieszanej liczby z niewłaściwej frakcji operacja mnożenia jest przeprowadzana jak zwykle:

Ćwiczenie 2

Wiek José to ½ 2/3 wieku Manuela. Jeśli Manuel ma 24 lata, jaki jest wiek José?

Rozwiązanie

Niech X wiek José, nieznany, że musimy znaleźć. Oświadczenie mówi nam, że wiek Manuela wynosi 24 lata, dlatego wartość ta jest znana.

Aby ustalić wiek José, przeprowadzamy operacje wskazane przez stwierdzenie: „Wiek José wynosi ½ 2/3 wieku Manuela”.

To jest pomnożenie dwóch frakcji dla liczby całkowitej:

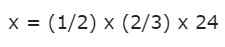
Możemy pomnożyć dwa pierwsze frakcje zgodnie z opisanymi wcześniej regułami. Ze swojej strony numer 24 jest liczbą całkowitą, ale już wiemy, że nie ma problemu z przekształceniem go w ułamek, po prostu poprzez umieszczenie 1 jako mianownika:

Możemy znacznie uprościć operację, obserwując, że 2 w licznikach drugiej frakcji jest natychmiast anulowane z 2, który jest mianownikiem w pierwszym.

Właśnie to pozostawiliśmy po odwołaniu:

Dlatego José ma 8 lat.

Bibliografia

1. Baldor, a. 1986. Arytmetyka. Codex Editions and Dystrybucje.
2. Carena, m. 2019. Podręcznik matematyki. National University of the Coast.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Sangaku Maths. Mnożenie ułamków. Odzyskany z: sangakoo.com.
5. Smartick. Mnożenie ułamków. Odzyskany z: Smartick.Jest.