Metodologia losowego pobierania próbek, zalety, wady, przykłady

On losowe pobieranie próbek Jest to sposób na wybranie statystycznie reprezentatywnej próby z danej populacji. Część zasady, że każdy element próbki musi mieć takie samo prawdopodobieństwo wyboru.

Loteria jest przykładem losowego pobierania próbek, w którym każdy członek populacji uczestników jest przypisywany liczbą. Aby wybrać liczby odpowiadające nagrodom loterii (próbka) używana jest losowa technika, na przykład wyodrębnia z skrzynki pocztowej liczby, które zostały ocenione na identycznych kartach.

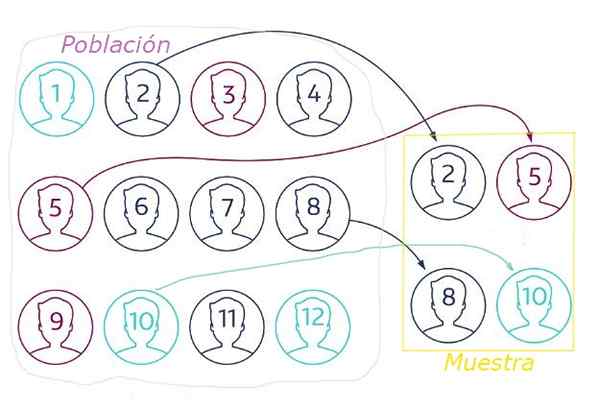Rysunek 1. W losowym pobieraniu próbek próbka jest wyodrębniana z losowej populacji za pomocą jakiejś techniki, która zapewnia, że ​​wszystkie elementy mają takie samo prawdopodobieństwo wybrania. Źródło: Netquest.com.

W losowym pobieraniu próbek jest niezbędne.

[TOC]

Rozmiar próbki

Istnieją wzory do określenia odpowiedniego rozmiaru próbki. Najważniejszym czynnikiem do rozważenia jest to, czy wielkość populacji jest znana. Spójrzmy na wzory, aby określić wielkość próby:

Przypadek 1: Wielkość populacji nie jest znana

Gdy wielkość populacji jest nieznana, możliwe jest wybranie odpowiedniej próby N, aby ustalić, czy pewna hipoteza jest prawdziwa, czy fałszywa.

W tym celu stosuje się następującą formułę:

n = (z² P q)/(e²)

Gdzie:

-P Jest to prawdopodobieństwo, że hipoteza jest prawdziwa.

-Q jest prawdopodobieństwem, że tak nie jest, dlatego q = 1 - p.

-E jest względnym marginesem błędu, na przykład 5% błąd ma margines e = 0,05. 

-Z ma związek z poziomem zaufania wymaganego przez badanie.

Może ci służyć: rozkład normalny: wzór, cechy, przykład, ćwiczenie

W rozkładu normalnym typowym (lub znormalizowanym) poziom ufności 90% ma z = 1645, ponieważ prawdopodobieństwo, że wynik wynosi między -1 445σ i +1645σ wynosi 90%, gdzie σ jest odchyleniem standardowym.

Poziomy zaufania i odpowiednie wartości Z 

1.- 50% poziom ufności odpowiada Z = 0,675.

2.- 68.3% poziom ufności odpowiada Z = 1.

3.- 90% poziom ufności równoważny Z = 1645.

4.- 95% poziom ufności odpowiada Z = 1,96

5.- 95,5% poziom ufności odpowiada Z = 2.

6.- 99,7% poziom ufności jest równoważny Z = 3.

Przykładem, w którym można zastosować tę formułę, byłby badanie w celu ustalenia średniej wagi kamyków plaży.

Najwyraźniej nie jest możliwe studiowanie i zważenie wszystkich kamyków plaży, więc jest to wygodne.

Rysunek 2. Aby zbadać charakterystykę kamyków plaży, konieczne jest wybranie losowej próbki z ich reprezentatywną liczbą. (Źródło: Pixabay)

Przypadek 2: Wielkość populacji jest znana

Gdy znana jest liczba N elementów składających się z pewnej populacji (lub wszechświata), jeśli chcesz wybrać przez proste losowe pobieranie próbek statystycznie istotnej próbki, jest to wzór: 

n = (z²p q n)/(n e² + Z²P Q)

Gdzie:

-Z jest współczynnikiem związanym z poziomem zaufania.

-P jest prawdopodobieństwem sukcesu hipotezy.

-Q jest prawdopodobieństwem niepowodzenia w hipotezie, p + q = 1.

-N jest wielkością całkowitej populacji.

-E jest względnym błędem wyniku badania.

Przykłady

Metodologia wyodrębniania próbek zależy wiele od rodzaju badań wymaganych. Dlatego losowe pobieranie próbek ma niezliczone zastosowania:

Może ci służyć: oznaki grupowania

Ankiety i kwestionariusze

Na przykład w ankietach telefonicznych ludzie są wybierani do konsultacji przez generator liczb losowych, mający zastosowanie do badanego regionu.

Jeśli chcesz zastosować kwestionariusz dla pracowników dużej firmy, wybór respondentów może być używany za pośrednictwem numeru pracownika lub numeru karty tożsamości.

Liczba ta musi być również wybierana losowo, na przykład przy użyciu generatora liczb losowych.

Rysunek 3. Kwestionariusz można zastosować losowo wybierając uczestników. Źródło: Pixabay.

QA

W przypadku, gdy badanie jest na części wyprodukowanych przez maszynę, części muszą być wybierane losowo, ale partii wytwarzanych w różnych porach dnia lub w różnych dniach lub tygodniach.

Zalety

Proste losowe pobieranie próbek:

- Pozwala na obniżenie kosztów badania statystycznego, ponieważ nie jest konieczne badanie całkowitej populacji w celu uzyskania statystycznie wiarygodnych wyników, z pożądanym poziomem zaufania i poziomem błędu wymaganego w badaniu.

- Unikaj stronniczości: Ponieważ wybór elementów, które należy zbadać.

Niedogodności

- Metoda nie jest odpowiednia w przypadkach, w których chcesz poznać preferencje w różnych grupach lub warstwach populacyjnych.

W takim przypadku lepsze jest wcześniej ustalenie grup lub segmentów, na których przeprowadzono badanie. Po zdefiniowaniu warstw lub grup, jeśli każdy z nich jest wygodny.

- Jest bardzo mało prawdopodobne, aby uzyskać informacje o sektorach mniejszościowych, których czasem konieczne jest znanie ich cech.

Może ci służyć: zasada Simpsona: formuła, demonstracja, przykłady, ćwiczenia

Na przykład, jeśli jest to kampania na kosztownym produkcie, konieczne jest znanie preferencji najbogatszych sektorów mniejszościowych.

Ćwiczenie rozwiązane

Chcemy zbadać preferencje populacji pod względem sposobu, w jaki Cola of Cola, ale nie ma wcześniejszych badań w tej populacji, z których jej wielkość jest nieznana.

Z drugiej strony próbka musi być reprezentatywna przy minimalnym poziomie ufności 90%, a wnioski muszą mieć procentowy błąd 2%.

-Jak określić rozmiar S próbki?

-Jaki byłby wielkość próbki, gdyby margines błędu jest wykonany do 5%?

Rozwiązanie

Ponieważ wielkość populacji jest nieznana, w celu ustalenia wielkości próbki, zastosowano wzór podany powyżej:

n = (z²P q)/(e²)

Zakładamy, że istnieje takie samo prawdopodobieństwo preferencji (p) przez nasze odświeżenie, że z braku (q), a następnie p = q = 0,5.

Z drugiej strony, ponieważ wynik badania musi mieć procentowy błąd mniejszy niż 2%, błąd względny wyniesie 0,02.

Wreszcie wartość Z = 1645 wytwarza poziom ufności 90%.

Krótko mówiąc, masz następujące wartości:

Z = 1645

P = 0,5

Q = 0,5

E = 0,02

Z tymi danymi obliczana jest minimalna wielkość próbki:

N = (1645² 0,5 0,5)/(0,02²) = 1691.3

Oznacza to, że badanie z wymaganym marginesem błędu i wybranym poziomem zaufania musi mieć próbkę respondentów co najmniej 1692 osób, wybranych przez proste losowe próbkowanie.

Jeśli przejdziesz od marży błędu z 2% do 5%, nowa wielkość próby to:

N = (1645² 0,5 0,5)/(0,05²) = 271

Co jest znacznie niższą liczbą osób. Podsumowując, wielkość próby jest bardzo wrażliwa na pożądany margines w badaniu.

Bibliografia

1. Berenson, m. 1985.Statystyki dotyczące administracji i gospodarki, koncepcje i zastosowania. Międzyamerykański redakcja.
2. Statystyka. Losowe pobieranie próbek. Zaczerpnięte z: Encyclopediaeconomica.com.
3. Statystyka. Próbowanie. Odzyskane z: statystyki.Mata.Nas na.MX.
4. Zadbany. Losowe pobieranie próbek. Odzyskane z: Odkazane.com.
5. Moore, d. 2005. Zastosowano podstawowe statystyki. 2. Wydanie.
6. Netquest. Losowe pobieranie próbek. Odzyskane z: Netquest.com.
7. Wikipedia. Próbowanie statystyczne. Źródło: w:.Wikipedia.org