Metoda Gauss-Seidel Objaśnienie, aplikacje, przykłady

On Metoda Gauss-Seidel Jest to iteracyjna procedura znalezienia przybliżonych rozwiązań dla układu liniowych równań algebraicznych z arbitralnie wybraną precyzją. Metoda ma zastosowanie do macierzy kwadratowej z elementami nie zerowymi w swoich przekątkach, a zbieżność jest gwarantowana, jeśli matryca jest dominująca po przekątnej.

Został stworzony przez Carla Friedricha Gaussa (1777–1855), który wykonał prywatną demonstrację jednemu z jego studentów w 1823 roku. Następnie został formalnie opublikowany przez Philipp Ludwig von Seidel (1821–1896) w 1874 r., Stąd nazwa obu matematyków.

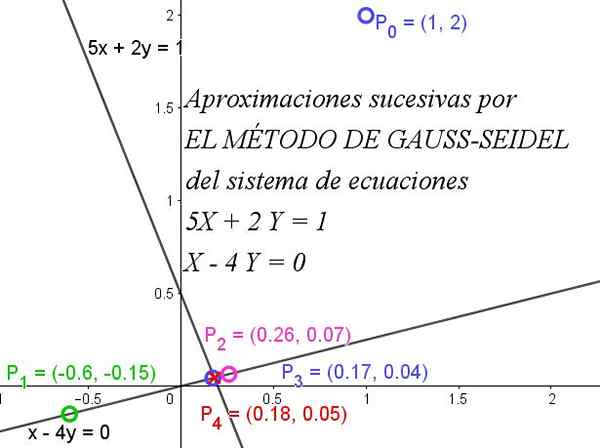
Rysunek 1. Metoda Gaussa-Seidela szybko zbiega się w celu uzyskania systemu równań. Źródło: f. Zapata.

Aby uzyskać pełne zrozumienie metody, należy wiedzieć, że macierz jest dominująca po przekątnej, gdy wartość bezwzględna elementu przekątnego każdego wiersza jest większa lub równa sumie wartości bezwzględnych innych elementów tego samego rządu.

Matematycznie wyraża się to w następujący sposób:

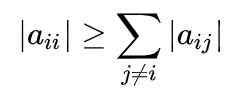
[TOC]

Objaśnienie poprzez prostą sprawę

Aby zilustrować, co metoda Gauss-Seidel weźmie proste przypadek, w którym można znaleźć wartości x i y w systemie równań liniowych 2 × 2 pokazanych poniżej:

5x + 2y = 1

X - 4y = 0

Kroki do naśladowania

1- Przede wszystkim musisz ustalić, czy konwergencja jest bezpieczna. Natychmiast obserwuje się, że w efekcie jest to system po przekątnej, ponieważ w pierwszym rzędzie pierwszy współczynnik ma większą wartość bezwzględną niż inne z pierwszego rzędu:

| 5 |> | 2 |

Podobnie, drugi współczynnik drugiego rzędu jest również dominujący po przekątnej:

| -4 |> | 1 |

2- Zmienne x i y są jasne: 

X = (1 - 2Y)/5

Y = x/4

3- Układa się początkową arbitralną wartość, zwaną „nasieniem”: xo = 1, me = 2.

4

Może ci służyć: oszacowanie według interwałów

X1 = (1 - 2 me)/5 = (1 - 2 × 2)/5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- Przejdź w podobny sposób, aby uzyskać drugie przybliżenie rozwiązania układu równań:

X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50 

Y2 = x2/4 = (13/50)/4 = 13/200

6- Trzecia iteracja:

X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500

Y3 = x3/4 = (87/500)/4 = 87/2000

7- Czwarta iteracja, jako ostateczna iteracja tego ilustracyjnego przypadku:

X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000

Y4 = x4/4 = (913/5000)/4 = 913/20000

Wartości te całkiem dobrze pokrywają się z rozwiązaniem znalezionym innymi metodami rozdzielczości. Czytelnik może to szybko sprawdzić za pomocą internetowego programu matematycznego.

Analiza metody

Jak widać, w metodzie Gauss-Seidel, przybliżone wartości uzyskane dla poprzedniej zmiennej w tym samym etapie należy wymienić w następującej zmiennej. Odróżnia go od innych metod iteracyjnych, takich jak Jacobi, w których każdy krok wymaga podejścia do poprzedniego etapu. 

Metoda Gaussa-Seidela nie jest procedurą równoległą, podczas gdy Gauss-Jordan jest. Jest to również powód, dla którego metoda Gauss-Seidel ma szybszą metodę bez konwergencji niż metoda Jordana.

Jeśli chodzi o warunki matrycy po przekątnej, nie zawsze jest to zadowolone. Jednak w większości przypadków wystarczy wymienić szeregi oryginalnego systemu, aby spełnić ten warunek. Ponadto metoda prawie zawsze zbiega się, nawet gdy warunek dominacji po przekątnej nie jest spełniony.

Poprzedni wynik, uzyskany przez cztery iteracje metody Gauss-Seidel, można zapisać w dziesiętne:

Może ci służyć: ile osi symetrii ma koło?

X4 = 0,1826

Y4 = 0,04565

Dokładne rozwiązanie systemu podniesionych równań to:

X = 2/11 = 0,1818

Y = 1/22 = 0,04545.

Zatem tylko z 4 iteracji uzyskano wynik z tysięczną precyzją (0,001).

Rysunek 1 ilustruje, w jaki sposób kolejne iteracje szybko zbiegają się z dokładnym rozwiązaniem.

Aplikacje

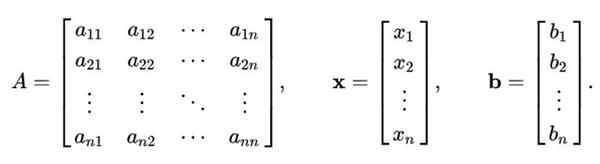
Metoda Gauss-Seidel nie jest ograniczona tylko do systemu równań liniowych 2 × 2. Powyższą procedurę można uogólnić w celu rozwiązania systemu liniowego N równania z N Nieznane, które są reprezentowane macierzowo, takie jak ten:

DO X = B

Gdzie DO To macierz n x n, chwila X Jest to wektor n składników zmiennych, które należy obliczyć; I B Jest to wektor, który zawiera wartości niezależnych terminów.

W celu uogólnienia sekwencji iteracji zastosowanych w przypadku ilustracyjnego do systemu n x n, który chce obliczyć zmienną Xi, Obowiązuje następujący formuła:

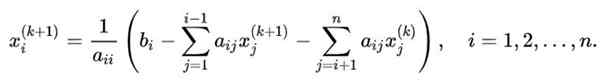
W tym równaniu:

- k Jest to wskaźnik wartości uzyskanej w iteracji k.

-K+1 Wskazuje nową wartość w następujących.

Ostateczna liczba iteracji jest określana, gdy wartość uzyskana w iteracji K+1 różni się od uzyskanych bezpośrednio wcześniej, w ilości ε, która jest dokładnie pożądaną precyzją.

Przykłady metody Gauss-Seidel

- Przykład 1

Napisz ogólny algorytm, który umożliwia obliczenie wektora przybliżonego rozwiązania X układu liniowego równań NXN, biorąc pod uwagę matrycę współczynnika DO, Wektor niezależnych warunków B, Liczba iteracji (iter) oraz początkowe lub „ziarno” wektora X.

Rozwiązanie

Algorytm składa się z dwóch „dla„ cykli ”, jednego dla liczby iteracji, a drugi dla liczby zmiennych. Byłoby to następujące:

Dla k ∊ [1 ... iter]

Bo ∊ [1… n]

X [i]: = (1/a [i, i])*(b [i] - ∑_{J = 1}^N(A [i, j]*x [j]) + a [i, i]*x [i])

Może ci służyć: notacja dziesiętna

- Przykład 2

Sprawdź działanie poprzedniego algorytmu, stosując się do oprogramowania matematycznego Studio Smath Bezpłatnie i bezpłatne, dostępne dla systemu Windows i Android. Weźmy na przykład przypadek matrycy 2 × 2, która służyła nam do zilustrowania metody Gaussa-Seidela.

Rozwiązanie

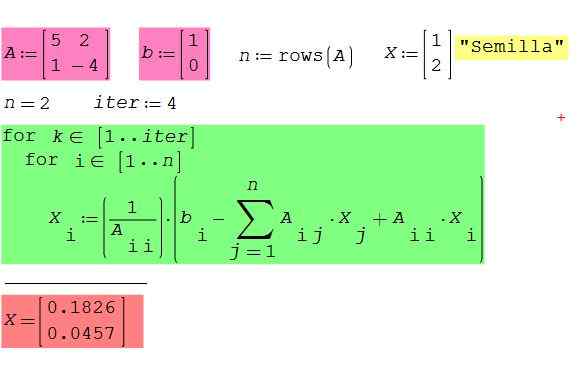Rysunek 2. System równań przykładu 2 x 2, przy użyciu oprogramowania Studio Smath. Źródło: f. Zapata.

- Przykład 3

Zastosuj algorytm Gaussa-Seidela dla następującego systemu równań 3 × 3, który wcześniej został uporządkowany w taki sposób, aby współczynniki przekątne dominują (to znaczy o większej wartości bezwzględnej niż wartości bezwzględne współczynników współczynników współczynników tego samego rządu):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Użyj wektora zerowego jako nasion i rozważ pięć iteracji. Skomentuj wynik.

Rozwiązanie

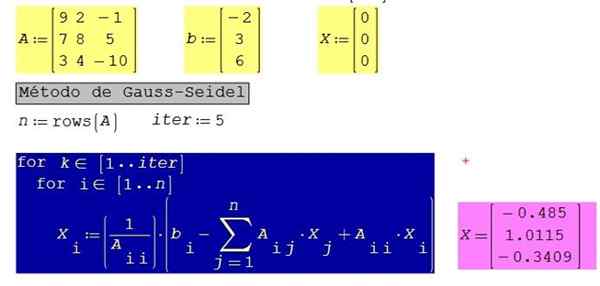Rysunek 3. Rozwiązanie układu równań rozdzielonego przykładu 3, przy użyciu SMATH Studio. Źródło: f. Zapata.

Dla tego samego systemu z 10 iteracami zamiast 5 uzyskano następujące wyniki: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

Wskazuje to, że wystarczy z pięcioma iteracji, aby uzyskać trzy precyzyjne dziesiętne i że metoda szybko przekazuje rozwiązanie.

- Przykład 4

Za pomocą podanego algorytmu Gaussa-Seidela znajdź rozwiązanie systemu równań 4 × 4, który występuje poniżej:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

Aby rozpocząć metodę, skorzystaj z tego ziarna:

x1 = 0, x2 = 0, x3 = 0 i x4 = 0

Rozważ 10 iteracji i oszacuj błąd wyniku, w porównaniu z numerem iteracji 11.

Rozwiązanie

Rysunek 4. Rozwiązanie układu równań rozdzielonego przykładu 4, przy użyciu SMATH Studio. Źródło: f. Zapata.

W porównaniu z następującą iteracją (numer 11) wynik jest identyczny. Największe różnice między dwoma iteracji są rzędu 2 × 10^-8, Co oznacza, że ​​pokazane rozwiązanie ma dokładność co najmniej siedmiu dziesiętnych.

Bibliografia

1. Iteracyjne metody rozwiązania. Gauss-Seidel. Odzyskane z: cimat.MX
2. Metody numeryczne. Gauss-Seidel. Odzyskane z: test.CUA.Uam.MX
3. Metoda numeryczna: Gauss-Seidel. Odzyskane od: Ucz się w linii.Ty.Edu.współ
4. Wikipedia. Metoda Gauss-Seidel. Źródło: w:. Wikipedia.com
5. Wikipedia. Metoda Gauss-Seidel. Odzyskane z: jest.Wikipedia.com