Metoda Eulera do zastosowania procedury i ćwiczeń

On Metoda Eulera Jest to najbardziej podstawowa i prosta procedury stosowane do znalezienia przybliżonych roztworów numerycznych, do zwykłego równania różniczkowego pierwszego rzędu, pod warunkiem, że jego początkowy stan jest znany.

Zwykłe równanie różniczkowe (EDO) to równanie, które wiąże nieznaną funkcję pojedynczej zmiennej niezależnej z jej pochodnymi.

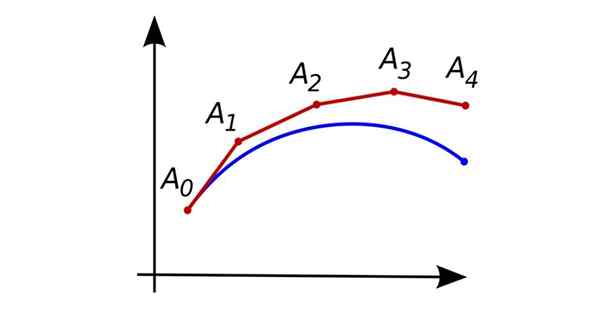
Kolejne podejścia metodą Eulera. Źródło: Oleg Alexandrov [domena publiczna]

Jeśli największa pochodna, która pojawia się w równaniu, jest stopień pierwotny, jest to zwykłe równanie różniczkowe pierwszego stopnia.

Najbardziej ogólnym sposobem pisania równania pierwszego stopnia jest:

Z początkowym warunkiem:

x = x₀

y = y₀

[TOC]

Jaka jest metoda Eulera?

Ideą metody Eulera jest znalezienie numerycznego rozwiązania równania różniczkowego w przedziale między x₀ i x_F .

Po pierwsze, przedział w punktach N+1 jest nie zgodzony:

X₀, X₁, X₂, X₃…, X_N

Które są uzyskiwane w ten sposób:
X_Siema= x₀+Ih

Gdzie H jest szerokością lub krokiem podinterwali:

Im większa liczba n, wynik będzie bardziej precyzyjny, ale potrzebna będzie większa liczba punktów, aby pokryć przedział, w którym szukamy rozwiązania, a czas obliczeniowy rośnie.

W warunkach początkowego można również poznać pochodną na początku:

i '(x_albo) = f (x_albo, I_albo)

Ta pochodna reprezentuje nachylenie stycznej linii do krzywej funkcji y (x) dokładnie w punkcie:

Ao = (x_albo, I_albo)

Wówczas przybliżone przewidywanie wartości funkcji y (x) jest dokonywane w następnym punkcie:

i (x₁) ≈ i₁

I_1 = I_albo +(X₁- X_albo) f (x_albo, I_albo) = y_{albo +} H F (x_albo, I_albo)

Kolejny przybliżony punkt rozwiązania, który odpowiadałby:

DO₁ = (x₁, I₁)

Procedura jest powtarzana w celu uzyskania kolejnych punktów

Może Ci służyć: Funkcja logarytmiczna: właściwości, przykłady, ćwiczenia

DO₂, DO₃…, X_N

Na rysunku pokazanym na początku niebieska krzywa reprezentuje dokładne rozwiązanie równania różniczkowego, a czerwony reprezentuje kolejne przybliżone punkty uzyskane w procedurze Eulera.

Rozwiązane ćwiczenia

Ćwiczenie 1

Siema) Być równaniem różniczkowym:

Z warunkiem początkowym x = a = 0; I_Do= 1

Korzystając z metody Eulera, uzyskaj przybliżone rozwiązanie I We współrzędnej x = b = 0.5, podział interwału [a, b] przy n = 5 części.

Rozwiązanie

Wyniki numeryczne są podsumowane w następujący sposób:

Gdzie stwierdzono, że rozwiązanie i wartość 0.5 to 1.4851.

UWAGA: W przypadku realizacji obliczeń, które zostały użyte Studio Smath, Bezpłatny program użytkowania.

Ćwiczenie 2

Ii) Kontynuując równanie różniczkowe ćwiczenia I), znajdź dokładne rozwiązanie i porównaj je z wynikiem uzyskanym metodą Eulera. Znajdź błąd lub różnicę między dokładnym wynikiem a przybliżonym.

Rozwiązanie

Z warunkiem początkowym x = a = 0; I_Do= 1
Dokładne rozwiązanie nie jest zbyt trudne do znalezienia. Wiadomo, że pochodną funkcji Sen (x) jest funkcja cos (x). Dlatego rozwiązaniem y (x) będzie:

i (x) = sin x + c

Aby spełnić warunek początkowy i (0) = 1, stała c musi być warta 1. Następnie dokładny wynik jest porównywany z przybliżonym:

Stwierdzono, że w obliczonym przedziale podejście ma trzy znaczące liczby dokładności.

Ćwiczenie 3

Iii) Rozważ równanie różniczkowe i jego początkowe warunki podane poniżej:

i '(x) =- y²

Z warunkami początkowymi x₀ = 0; I₀ = 1

Użyj metody Eulera, aby znaleźć przybliżone wartości rozwiązania i (x) W przedziale x = [0, 1.5]. Użyj kroku H = 0.1.

Rozwiązanie

Metoda Eulera jest bardzo wskazana do zastosowania w arkuszu kalkulacyjnym. W takim przypadku użyjemy arkusza kalkulacyjnego Geogebra, Bezpłatny i bezpłatny program użytkowania.

Może ci służyć: proporcjonalność złożona: wyjaśnienie, trzy złożone reguły, ćwiczenia

Trzy kolumny (A, B, C) pokazano w arkuszu kalkulacyjnym rysunku X , Druga kolumna reprezentuje zmienną I, i trzecia kolumna pochodna I'.

Rząd 2 zawiera wartości początkowe X, I, I' .

Wartość wartości 0.1 Został umieszczony w komórce absolutnej pozycji (4 USD).

Początkowa wartość Y0 znajduje się w komórce B2, a Y1 w komórce B3. Do obliczenia i₁ Stosuje się formułę:

I_1 = I_albo +(X₁- X_albo) f (x_albo, I_albo) = y_{albo +} H F (x_albo, I_albo)

Ta formuła arkusza kalkulacyjnego byłaby liczbą B3: = B2 + $ D 4 $ * c3.

Podobnie Y2 byłby w komórce B4, a jego wzór pokazano na poniższym rysunku:

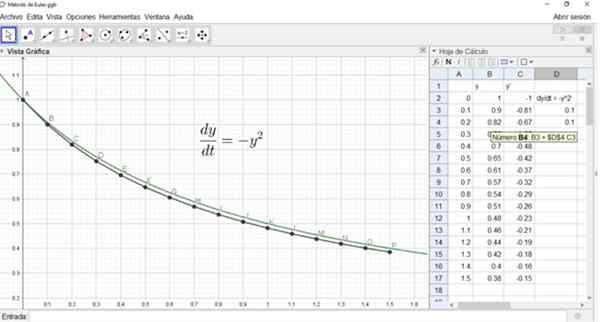
Rysunek pokazuje również wykres dokładnego rozwiązania, a punkty a, b, ..., p przybliżone rozwiązanie za pomocą metody Eulera.

Newton Dynamics and Euler's Method

Klasyczna dynamika została opracowana przez Isaaca Newtona (1643–1727). Oryginalna motywacja Leonarda Eulera (1707–1783) do opracowania jego metody było właśnie rozwiązanie równania drugiego prawa Newtona w różnych sytuacjach fizycznych.

Drugie prawo Newtona jest często wyrażane jako wtórne równanie różniczkowe:

Gdzie X reprezentuje w tej chwili pozycję obiektu T. Ten obiekt ma masę M i jest poddawany sile F. Funkcja F Jest to związane z siłą i masą w następujący sposób:

 Chociaż zasadniczo metoda Eulera została zaprojektowana w celu rozwiązania pierwszego stopnia równań różniczkowych, można ją łatwo rozszerzyć na drugą liczbę osób, ponieważ jest ona równoważna układowi dwóch równań pierwszego stopnia.

Może ci służyć: geometria analityczna

Aby zastosować metodę Eulera, wymagane są początkowe wartości czasu T, prędkość v i pozycja X.

Poniższa tabela wyjaśnia, w jaki sposób od wartości początkowych T1, v1, x1 można uzyskać przybliżenie prędkości v2 i pozycji x2, w momencie t2 = t1+δt, gdzie δt reprezentuje niewielki wzrost i odpowiada kroku. W metodzie Eulera.

Ćwiczenie 4

Iv) Jednym z podstawowych problemów w mechanice jest blok masy m powiązany ze sprężyną (lub sprężyną) stałej k.

Drugie prawo Newtona dla tego problemu byłoby takie:

W tym przykładzie, aby go uprościć, zostanie pobrane M = 1 i K = 1. Znajdź przybliżone rozwiązania pozycji X I prędkość v Metodą Eulera w przedziale czasowym [0, π/2] podział przedziału w 12 częściach.

Weź 0 jako moment początkowy, prędkość początkowa 0 i pozycja początkowa 1.

Rozwiązanie

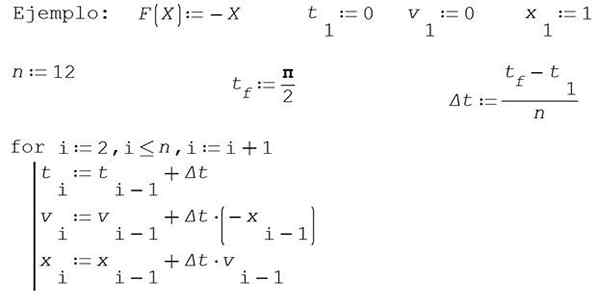
Wyniki liczbowe pokazano w poniższej tabeli:

Pokazane są również grafika pozycji i prędkość między instantami 0 i 1.44.

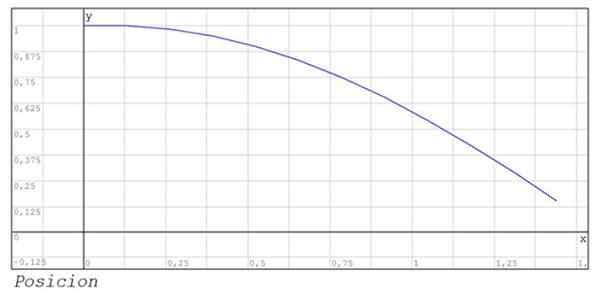
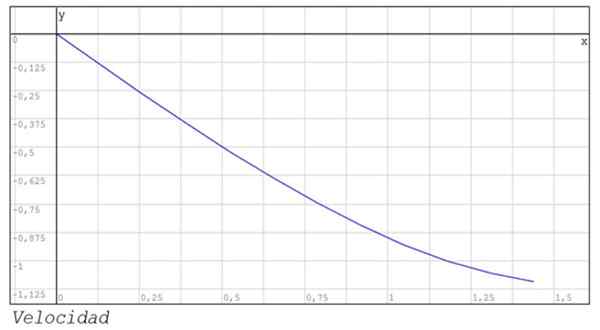
Proponowane ćwiczenia dla domu

Ćwiczenie 1

Użyj arkusza kalkulacyjnego, aby określić przybliżone rozwiązanie przy użyciu metody Eulera dla równania różniczkowego:

i '= -exp (-y) z warunkami początkowymi x = 0, y = -1 w przedziale x = [0, 1]

Zacznij od etapu 0,1. Wykres wynik.

Ćwiczenie 2

Korzystając z arkusza kalkulacyjnego, znajdź roztwory numeryczne do następującego równania drugiego stopnia, gdzie jest to funkcja zmiennej niezależnej T.

i "= - 1/y² z warunkami początkowym t = 0; y (0) = 0,5; i '(0) = 0

Znajdź roztwór w przedziale [0,5; 1.0] przy użyciu etapu 0,05.

Wykres wynik: i vs t; i „vs t

Bibliografia

1. Metoda Eurlera.Zaczerpnięte z Wikipedii.org
2. Euler Solver. Pochodzi z.Smath.com