Jednolity ruch kołowy (m.C.LUB.) Formuły, cechy

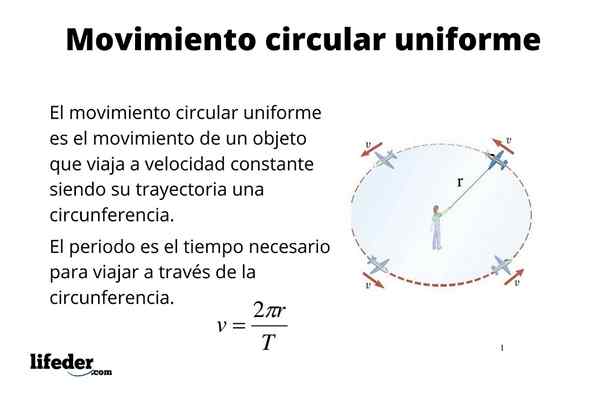
Cząstka ma Ruch okrągły mundur (M.C.LUB.) Gdy jego trajektoria jest obwodem, a także ciągle go podróżuje. Na przykład liczne obiekty, takie jak elementy maszyn i silników, mają ten rodzaj ruchu, w tym twarde dyski komputerów, fenatery, osie i wiele innych rzeczy są więcej.

Jednolity ruch kołowy jest również dobrym podejściem do ruchu niektórych ciał niebieskich, takich jak Ziemia. Orbita Ziemi jest naprawdę eliptyczna, jak wskazują prawa Keplera. Jednak mimośrodowość orbity jest niewielka i jako pierwsze podejście można uznać za okrągłe, co upraszcza niektóre obliczenia, takie jak znalezienie prędkości ziemi, gdy porusza się po słońcu.

W opisie jednolitego ruchu kołowego stosuje się te same parametry jak w ruchu prostoliniowym, a mianowicie: pozycja, przemieszczenie, czas, prędkość i przyspieszenie.

Przyśpieszenie? Tak, w efekcie jednolity ruch kołowy jest przyspieszany, nawet gdy jego prędkość v być stałe. To dlatego, że prędkość v, Że jest wektorem i dlatego jest odważny, nieustannie zmienia swój kierunek, gdy obiekt lub cząsteczka się obraca. Każda zmiana v Jest wytwarzany przez przyspieszenie, które, jak będzie widać, jest skierowane w kierunku środka trajektorii kołowej.

Jednolity ruch kołowy jest ruchem w płaszczyźnie Xy, Dlatego jest to ruch dwuwymiarowy. Możliwe jest jednak wygodniejsze wyrażanie go przez kąt θ, który zamiatuje cząstkę, mierzoną w odniesieniu do osi poziomej lub innej odpowiedniej osi odniesienia.

Nawet jeśli jest to rozszerzony obiekt, jego cząstki zawsze zamiatają ten sam kąt, nawet jeśli mają różne współrzędne (X, y).

[TOC]

Charakterystyka jednolitego ruchu okrągłego

Możesz podsumować charakterystykę jednolitego ruchu kołowego w następujący sposób:

-Trajektoria jest obwodem, dlatego jest ruch w płaszczyźnie.

-Prędkość v To jest stałe, ale prędkość v Nie, ponieważ nieustannie zmienia kierunek i znaczenie, aby pomieścić zakręt telefonu komórkowego.

-Wektor prędkości v Zawsze jest styczny do obwodu i prostopadły do ​​kierunku promieniowego.

-Prędkość kątowa ω jest stała.

-Pomimo tego, że jest jednolity, istnieje przyspieszenie, aby wyjaśnić te zmiany w kierunku prędkości. To przyspieszenie jest przyspieszeniem dośrodkowym.

-Przyspieszenie i prędkość dośrodkowe są prostopadłe.

-Jest to okres okresowy lub powtarzalny, dlatego okres i częstotliwość wielkości są dla niego zdefiniowane.

Jednolite formuły ruchu okrągłego

W tym schemacie występuje spin cząsteczki p v pociągnięty.

Może ci służyć: pole magnetyczne Ziemi: pochodzenie, cechy, funkcja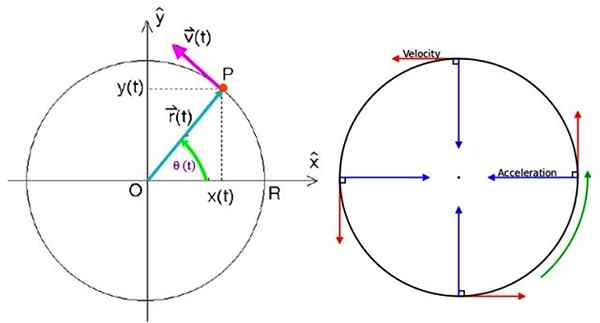 Jednolite parametry ruchu okrągłego. Źródło: f. Zapata/wikimedia Commons.

Aby określić wektor pozycji, konieczne jest.

Wektor pozycji

Jest oznaczony jako r (t) i jest skierowany od pochodzenia do punktu p, w którym znajduje się cząstka. W jednej chwili, we współrzędnych kartezjańskich, jest to napisane jako:

R (t) = x (t) Siema + oraz T) J

Gdzie Siema I J Są to wektory jednostek prostopadłych w kierunku X I I odpowiednio. Wykresu obserwuje się, że moduł wektorowy R (t) Zawsze w porządku R, Promień obwodu. Jeśli θ jest kątem, który tworzy R Z osą poziomą pozycja jest również równa:

R (t) = [RCOS θ(T)] Siema +[Rsen θ(T)] J

Kąt, który tworzy R (T) Z poziomą poziomą jest to kąt centralny, a jej wartość to:

θ = s/r

Gdzie S jest łukiem obwodu, a r radio. Wspomniany kąt θ To funkcja czasu, więc możesz pisać θ = θ (T), dzwonić pozycja kątowa.

Ponieważ prędkość jest stała, cząstka opisuje równe kąty w równych czasach i w analogii z jednolitym ruchem prostoliniowym, jest napisane:

θ = θ (t) = θ_albo + ωt

Tutaj θ_albo Jest to początkowe kąt mierzony w radianach w odniesieniu do osi odniesienia, może wynosić 0 lub dowolną wartość, a ω jest prędkością kątową.

Prędkość kątowa i prędkość liniowa

Prędkość kątowa jest pierwsza pochodząca z pozycji kątowej i jest oznaczona jako ω. Jego wartość jest stała dla jednolitego ruchu kołowego, ponieważ równe kąty są ogrodzenie w równych czasach. Innymi słowy:

Prędkość kątowa występuje w jednostkach radian/s. Ze swojej części prędkość liniowa jest obliczana przez:

Prędkość liniowa to moduł lub wielkość prędkości liniowej, która zmienia się, gdy cząstka obraca się po trajektorii. Kierunek prędkości jest zatem adresem stycznym do obwodu.

Jednostki prędkości liniowej w jednolitym ruchu okrągłym są takie same jak w przypadku ruchów liniowych: m/s (w systemie międzynarodowym SI), km/h, cm/s i innych.

Przyspieszenie dośrodkowe

Na poniższym rysunku istnieje cząstka, która porusza się w harmonogramie obwodu ze stałą prędkością. Oznacza to, że wektor prędkości ma zawsze ten sam moduł, ale zmienia kierunek, aby pomieścić obwód.

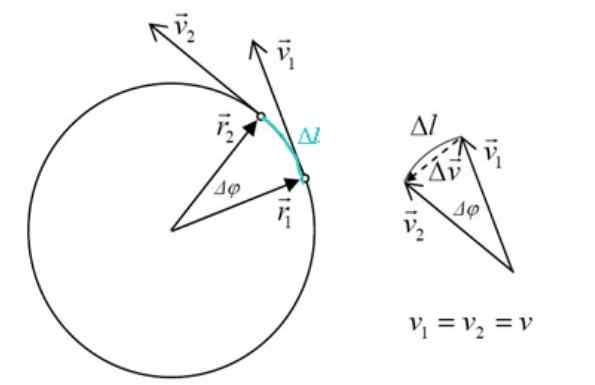Prędkość i przyspieszenie w jednolitym ruchu okrągłym. Źródło: f. Zapata.

Każda zmiana prędkości wyniki na przyspieszenie, które z definicji to:

Może ci służyć: 31 rodzajów siły w fizyce i ich cechy

Na powyższym obrazie znajduje się odejmowanie wśród wektorów v₂ I v₁, którego rezultatem jest δv, wektor proporcjonalny do przyspieszenia. Jak widać, zawsze wskazuje na środek obwodu i dlatego nazywa się go przyspieszeniem dośrodkowym lub przyspieszeniem promieniowym.

Trójkąt utworzony przez v₂, v₁ i δv Jest podobny do trójkąta boków R₂, R₁ i δL, Będąc φφ kątem centralnym. Wielkości R₂ I R₁ Są takie same, więc:

R₂ = r₁ = r

Następnie obu trójkątów są te relacje dla kąta:

Φφ = δr / r; Φφ = δv / v

BOLD nie są konieczne, ponieważ miara kąta zależy od wielkości tych wektorów. Wyrównanie powyższych wyrażeń następuje:

 Więc:

Dzielenie po obu stronach przez ΔT, aby uzyskać wielkość przyspieszenia:

Ale δR / δT to wielkość prędkości, zwanej v, W związku z tym:

Wreszcie przyspieszenie dośrodkowe jest:

Okres i częstotliwość

Ponieważ ruch kołowy jest powtarzalny, okres jest zdefiniowany T tego samego, co czas potrzebny na telefon, aby uzyskać pełny obrót. Ponieważ długość promienia promienia r wynosi 2πr, kąt zmieciał się w promieniach podczas kompletnego obracania, wynosi 2π radian i wymaga czasu t, prędkość kątowa wynosi:

Ω = 2π / t

T = 2π / ω

Okres jednolitego ruchu okrągłego mierzy się w ciągu kilku sekund w systemie międzynarodowym.

Ze swojej strony częstotliwość F Jest to liczba zakrętów na jednostkę czasu i jest wzajemną lub odwrotną okresem:

F = n /t = 1 /t

Jednostka częstotliwości w systemie międzynarodowym jest s^-1.

Przykłady jednolitego ruchu okrągłego

Wiele obiektów obraca się, aby uzyskać różnorodne efekty: koła, dyski i turbiny. Po osiągnięciu prędkości roboczej obrót jest zwykle przeprowadzany ze stałą prędkością. Ruch okrągły jest tak powszechny w życiu codziennym, że prawie nigdy o tym nie myślisz, więc oto kilka bliskich przykładów, które ilustrują to bardzo dobrze:

Ruch Ziemi

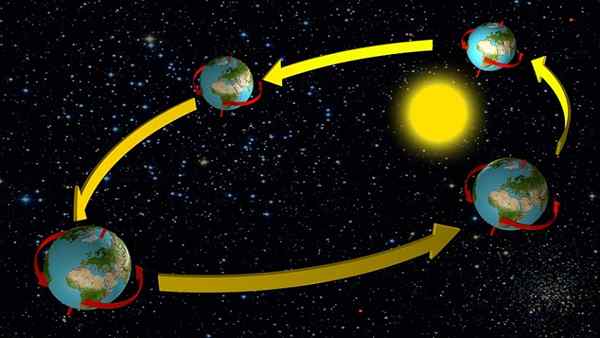
Ziemia i inne planety Układu Słonecznego poruszają się w eliptycznych trajektoriach małej mimośrodowości, z wyjątkiem rtęci, co oznacza, że ​​w pierwszym podejściu można założyć, że jego ruch jest jednolity okrąg.

Ma to dobry pomysł na szybkość tłumaczenia wokół Słońca, ponieważ w przypadku ziemi okres ruchu jest znany: rok lub 365 dni.

Cząstki na krawędzi albumu

Cząstki, które obracają się na krawędzi starożytnych r toadiscos lub moda wentylatora, podążają za jednolitym ruchem okrągłym, gdy urządzenie osiągnie prędkość reprodukcji.

Może ci służyć: Model atomowy Dirac Jordan: Charakterystyka i postulaty

Kosmiczny teleskop Hubble

Hubble Space Telescope wiruje wokół Ziemi na około 7550 m/s.

Odśrodki

Pralki przeprowadzają odwirowany proces wyciskania ubrań, który polega na obracaniu bębna pojemnika z dużą prędkością. Suszarki również obracają się przez pewien czas z jednolitym ruchem okrągłym.

Odwirowanie jest również stosowane w laboratoriach do oddzielania związków, a tym samym oddzielenie jego składników przez różnicę w gęstościach. Ilekroć mówi się o odwirowaniu, istnieje ruch okrągły, który jest jednolity, przynajmniej przez chwilę.

Prysznice ogrodowe

Wiele pryszniców ogrodowych nieustannie obraca się do ziemi w wodę w kilku.

Sporty

Na przykład w start młotku, który jest dyscypliną olimpijską, sportowiec obraca metalową kulkę ze stalowym kablem przymocowanym do uchwytu. Celem jest wysłanie piłki jak najdalej, ale bez opuszczenia określonego obszaru.

Ćwiczenie rozwiązane

Cząstka porusza się w okręgu o promieniu 2 m o stałej prędkości v = 8 m/s, w przeciwnym kierunku do zegara. Początkowo cząstka była w R = +2 J M. Oblicz:

a) Prędkość kątowa ω

b) jego pozycja kątowa θ (t)

c) okres ruchu

d) przyspieszenie dośrodkowe.

e) Pozycja cząstki po przejściu t = π/4 s

Rozwiązanie

Ze wzoru v = rω następuje:

Ω = v/r = (8 m/s)/2m = 4Rad ∙ s^-1

Rozwiązanie b

Przyjmując jako oś odniesienia do dodatniej osi x, cząstka początkowo wynosi 90º = π/2 w odniesieniu do wspomnianej osi, ponieważ stwierdzenie mówi, że położenie początkowe wynosi +2 J m, to znaczy cząsteczka jest w y = 2m, gdy ruch zacznie podążać.

θ = θ (t) = θ_albo + ωt = π/2 + 4t

Rozwiązanie c

T = 2π / ω = 2π / 4 s = 0.5 π s

Rozwiązanie d

a = v² / R = (8 m/ s)² / 2 m = 32 m/ s²

Rozwiązanie e

θ (t) = π/2 + 4T → θ (π/4) = π/2 + 4 ∙ (π/4) = 3π/2 Radian

Oznacza to, że po tym czasie cząstka jest w pozycji y = -2m J. Ma to sens, ponieważ t = π/4 s to połowa okresu, dlatego cząstka zwiedzała kąt 180º w sensie antyhorarycznym od jej początkowej pozycji i musi być właściwa w przeciwnej pozycji.

Bibliografia

1. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
3. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. osoba.
4. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.
5. Zapata, f. Ruch okrągły. Odzyskane z: Francessphysics.Blogspot.com.