Moment skrętny

Wyjaśniamy, jaki jest czas skrętny, jego cechy, wzory, jednostki, zastosowania i ćwiczenia do rozwiązania

Jaki jest czas skrętny?

On Moment skrętny, moment obrotowy lub moment siły to zdolność siły do ​​spowodowania zakrętu. Etymologicznie nazywa się to momentem obrotowym jako wyprowadzenie angielskiego słowa Moment obrotowy, z łaciny Torquere (skręcać).

Czas skrętnego (w odniesieniu do określonego punktu) jest wielkością fizyczną, która wynika z wykonywania produktu wektorowego między wektorami pozycji punktu, w którym siła jest przyłożona, a siłą wywieraną (we wskazanej kolejności). Ten moment zależy od trzech głównych elementów.

Pierwszym z tych pierwiastków jest wielkość przyłożonej siły, druga to odległość między punktem, w którym stosuje się, a punktem w odniesieniu do ciała obraca się (zwane również ramieniem dźwigni), a trzeci element to zastosowanie kąt wspomniana siła.

Większa siła, większy zwrot jest spowodowany. To samo dotyczy ramienia dźwigni: im większa odległość między punktem, w którym siła i punkt są stosowane w odniesieniu do tego wytworzonego przez zakręt, tym większe będzie to.

Logicznie, czas skrętki jest szczególnie interesujący w budownictwie i przemysłu, a także obecny w niezliczonych aplikacjach domowych, na przykład gdy orzech jest wyciswiony na angielskim kluczu.

Formuły

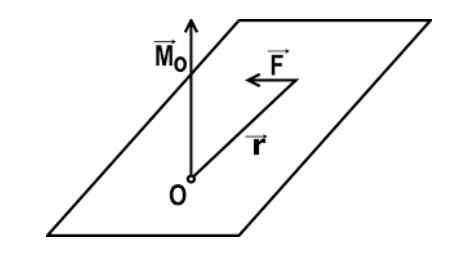
Matematyczne wyrażenie momentu skrętnego siły w stosunku do punktu lub jest podane przez: m = r x f

W tym wyrażeniu r jest wektorem, który łączy punkt O z punktem P zastosowania siły, a F jest wektorem przyłożonej siły.

Jednostki miary momentu to N ∙ m, które choć wymiarowo równoważne lipcu (j), mają inne znaczenie i nie należy ich pomylić.

Dlatego moduł momentu momentu obrotowego przyjmuje wartość podaną przez następujące wyrażenie:

M = r ∙ f ∙ Sen α

W tym wyrażeniu α jest kątem między wektorem wytrzymałościowym a wektorem r lub ramię dźwigni. Czas skrętu jest uważany za pozytywny, jeśli ciało obraca się w przeciwnym kierunku do igieł zegarowych; Przeciwnie, jest to negatywne, gdy zmienia się w harmonogramie.

Jednostki

Jednostka miary skręcania jest iloczyn jednostki siły przez jednostkę odległości. W szczególności w międzynarodowym systemie jednostek używane jest metro Newton, którego symbol to n • m.

Na poziomie wymiarowym metro Newton może wydawać się równoważne z lipcem; Jednak w żadnym wypadku nie należy użyć lipca do wyrażenia chwil. Lipiec to jednostka do pomiaru prac lub energii, która z koncepcyjnego punktu widzenia bardzo różnią się od momentów skrętnych.

Podobnie moment skrętu przedstawia charakter wektorowy, który jest zarówno energią pracy, jak i skalą.

Charakterystyka momentu skrętnego

Z widocznego wynika, że ​​moment skręcenia siły w stosunku do punktu reprezentuje zdolność siły lub zestawu sił do modyfikacji obrotu wspomnianego ciała wokół osi, która przechodzi przez punkt.

Dlatego moment skrętnego generuje przyspieszenie kątowe na ciele i jest wielkością charakteru wektora (więc jest on zdefiniowany z modułu, kierunku i zmysłu), który jest obecny w mechanizmach poddanych skręceniu lub zgięciu.

Czas skrętny będzie nieważny, jeśli wektor siły i wektor r mają ten sam kierunek, ponieważ w takim przypadku wartość Sen α będzie nieważna.

Wynikowy moment obrotowy

Biorąc pod uwagę pewne ciało, na którym działają siły serii, jeżeli siły stosowane działają w tej samej płaszczyźnie, moment skrętu wynikający z zastosowania wszystkich tych sił; Jest to suma momentów skręcania w wyniku każdej siły. Dlatego spełnia się, że:

M_T = ∑ m = m₁ + M_{2 +} M₃ +..

Oczywiście należy wziąć pod uwagę kryterium znaków na momenty skrętne, jak wyjaśniono powyżej.

Aplikacje

Moment obrotowy jest obecny w aplikacjach tak codziennie, jak ściskanie orzechów z angielskim kluczem lub otwieranie lub zamykanie kranu lub drzwi.

Jednak twoje aplikacje idą znacznie dalej; Czas skrętu znajduje się również w osiach maszyny lub w wyniku wysiłków, na które belki są poddawane. Dlatego jego zastosowania w branży i mechanice są liczne i różnorodne.

Rozwiązane ćwiczenia

Poniżej znajduje się kilka ćwiczeń, aby ułatwić zrozumienie wyjaśnień.

Ćwiczenie 1

Biorąc pod uwagę następującą liczbę, w której odległości między punktem O i punkty A i B wynoszą odpowiednio 10 cm i 20 cm:

a) Obliczyć wartość modułu momentu obrotowego w stosunku do punktu lub jeśli siła 20 N jest przyłożona w punkcie A.

b) Obliczyć, jaka powinna być wartość siły przyłożonej w B w celu osiągnięcia tego samego czasu skrętu, który uzyskano w poprzednim rozdziale.

Rozwiązanie

Po pierwsze, dane dla międzynarodowych jednostek systemowych powinny minąć.

R_DO = 0,1 m

R_B = 0,2 m

a) Aby obliczyć moment skrętny, używamy następującego wzoru:

M = r ∙ f ∙ Sen α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m

b) Aby ustalić żądaną siłę, kontynuuj w podobny sposób:

M = r ∙ f ∙ Sen α = 0,2 ∙ f ∙ 1 = 2 N ∙ m

Oczyszczanie F Jest uzyskiwane, że:

F = 10 n

Ćwiczenie 2

Kobieta wykonuje siłę 20 N na końcu angielskiego klucza o długości 30 cm. Jeśli kąt siły z klawiszem klucza wynosi 30 °, jaki jest czas skrętu w nakrętce?

Rozwiązanie

Zastosowana jest następująca formuła i działa:

M = r ∙ f ∙ Sen α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m