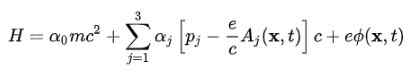Model Aomic o cechach i postulatach Dirac Jordan

On Model atomowy Dirac-jorda Jest to relatywistyczne uogólnienie operatora Hamiltonian w równaniu opisującym funkcję fali kwantowej. W przeciwieństwie do poprzedniego modelu, Schrodingera, nie jest konieczne nałożenie obrotu przez zasadę wykluczenia Pauli, ponieważ pojawia się on naturalnie.

Ponadto model Dirac-jordanu zawiera korektę relatywistyczną, interakcję spin-narząd i termin Darwina, które uwzględniają drobną strukturę poziomów elektronicznych atomu.

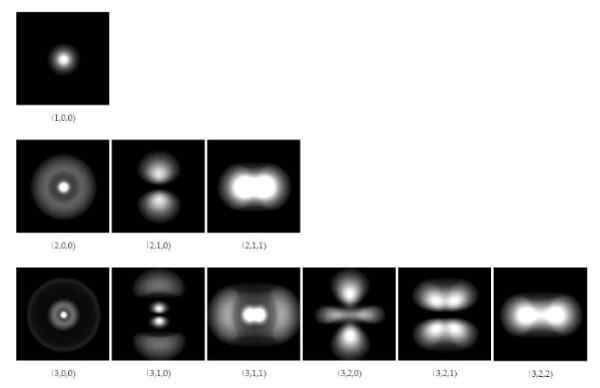
Rysunek 1. Orbitale elektroniczne w atomie wodoru dla pierwszych trzech poziomów energii. Źródło: Wikimedia Commons.

Od 1928 r. Naukowcy Paul A. M. Dirac (1902-1984) i Pascual Jordan (1902-1980) zostały zaproponowane do uogólnienia mechaniki kwantowej opracowanej przez Schrodingera, w celu uwzględnienia poprawek specjalnej względności Einsteina.

Część równania Schrodingera, która składa się z operatora różnicowego, zwanego Hamiltonianem, który działa na funkcji znanej jako Funkcja fali elektronowej. Schrodinger nie wziął jednak pod uwagę efektów relatywistycznych.

Rozwiązania funkcji fali pozwalają obliczyć regiony, w których elektron wokół jądra będzie znaleziony z pewnym stopniem prawdopodobieństwa. Te regiony lub obszary są nazywane Orbitale I zależą od niektórych dyskretnych liczb kwantowych, które definiują energię i pęd kątowy elektronu. 

[TOC]

Postuluje

W kwantowych teoriach mechanicznych, relatywistycznych, czy nie, nie ma pojęcia orbit, ponieważ ani pozycja, ani prędkość elektronu nie można określić jednocześnie. A ponadto określenie jednej z zmiennych prowadzi do całkowitej niedokładności w drugiej.

Ze swojej strony Hamiltonian jest operatorem matematycznym, który działa w funkcji fali kwantowej i jest zbudowany z energii elektronów. Na przykład wolny elektron ma całkowitą energię, co zależy od jego liniowego pędu P zatem:

E = (P²)/ 2M

Aby zbudować Hamiltonian, zaczyna się od tego wyrażenia i zostaje zastąpiona P Przez operatora kwantowego dla pędu: 

P = -I ħ ∂ /∂R 

Należy zauważyć, że warunki P I P Są różne, ponieważ pierwszy to pęd, a drugi to Operator różnicowy związane z pędem. 

Może ci służyć: model atomowy Leukipo: postulaty, ograniczenia, znaczenie

Dodatkowo i jest wyimaginowaną jednostką i ħ stała Plancka podzielona przez 2π, w ten sposób uzyskuje się operator Hamiltonian H wolnego elektronu:

H = (ħ²/2m) ∂² /∂R² 

Aby znaleźć Hamiltonian elektronu w atomie, dodano interakcję elektronów z jądrem: 

H = (ħ2/2m) ∂² /∂R²  - Eφ (r)

W poprzednim wyrażeniu -E jest ładunek elektronowy elektronowy i φ (r) potencjał elektrostatyczny wytwarzany przez jądro centralne.

Teraz operator H działa na funkcję falową ψ zgodnie z równaniem Schrodingera, które jest napisane w ten sposób:

H ψ = (i ħ ∂ /∂t) ψ

Cztery postulaty Dirac

Pierwszy postulat: Równanie fali relatywistycznej ma tę samą strukturę co równanie fali Schrodingera, jakie zmiany to h:

H ψ = (i ħ ∂ /∂t) ψ

Drugi postulat: Operator Hamiltonian został zbudowany na podstawie relacji Einsteina Energy-Momentum, który jest napisany w ten sposób:

E = (m² C⁴ + P² C²)^1/2

W poprzednim związku, jeśli cząstka ma pęd p = 0, to masz słynne równanie e = mc² który odnosi energię spoczynkową dowolnej masy m z prędkością światła c.

Trzeci postulat: Aby uzyskać operator Hamiltonian, zastosowano tę samą regułę kwantyzacji zastosowaną w równaniu Schrodingera:

P = -I ħ ∂ /∂R

Na początku nie było jasne, jak poradzić sobie z tym różnicowym operatorem działającym w rdzeniu kwadratowym, więc Dirac wyruszył do uzyskania liniowego operatora Hamiltoniana w operatorze pędu, a stamtąd powstał jego czwarty postulat.

Postulujący pokój: Aby pozbyć się pierwiastka kwadratowego w relatywistycznym wzorze energetycznym, Dirac zaproponował następującą strukturę dla E²:

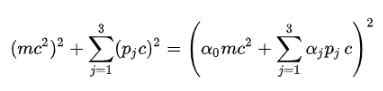
Oczywiście konieczne jest określenie współczynników alfa (α0, α1, α2, α3), aby się to spełniło.

Równanie Dirac

Równanie DIRAC zostało najpierw podniesione dla wolnego elektronu, przy użyciu struktury zaproponowanej w czwartym postulatu. Pozostaje następująco: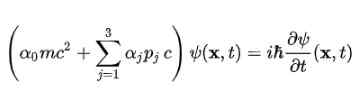

Może ci służyć: usłyszę sił: siły powierzchniowe i masowe

W swojej zwartej postaci równanie Dirac jest uważane za jedno z najpiękniejszych równań matematycznych na świecie:

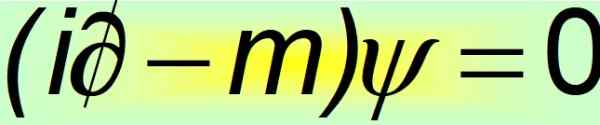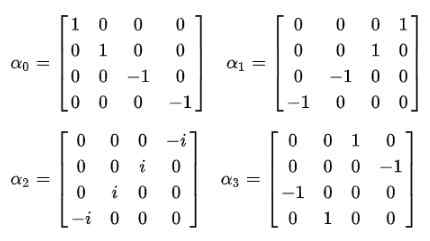
Rysunek 2. Równanie Dirac Compact. Źródło: f. Zapata.

I wtedy dowodzi, że stałe alfas nie mogą być ilościami skalarnymi. Jedynym sposobem, w jaki równość czwartego postulatu jest wypełniona, jest to, że mają to 4 × 4 stałe macierze, które są znane jako Matryce Dirac:

Natychmiast zaobserwowano, że funkcja fali przestaje być funkcją skalarną i staje się wektorem czterokomponowym Espinor:

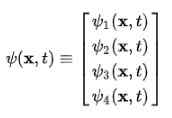
Atom Dirac-Jordana

Aby uzyskać model atomowy, konieczne jest przejście od równania wolnego elektronu do równania elektronu w polu elektromagnetycznym wytwarzanym przez jądro atomowe. Ta interakcja jest brana pod uwagę poprzez włączenie potencjalnego skalaru φ i potencjalnego wektora DO W Hamiltonian:

Funkcja fali (ESPINOR), która wynika z włączenia tego Hamiltoniana, ma następujące cechy: 

- Spełnia specjalną teorię względności, ponieważ uwzględnia wewnętrzną energię elektronu (pierwszy termin relatywistycznego hamiltonianu)

- Ma cztery rozwiązania odpowiadające czterem komponentom Espinor

- Pierwsze dwa rozwiązania odpowiadają jednemu do spin +½, a drugie do spinu - ½ 

- Wreszcie pozostałe dwa rozwiązania przewidują istnienie antymaterii, ponieważ odpowiadają one pozitronom przeciwieństw.

Ogromną zaletą równania Dirac jest to, że podstawowe korektę Hamiltonowskie Schrodingera H (O) można podzielić na kilka terminów, które pokażemy poniżej:

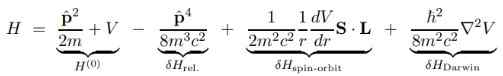
W poprzednim wyrażeniu v jest potencjalnym skalarnym, ponieważ potencjalny wektor DO Jest nieważny, jeśli ma to do centralnego stacjonarnego protonu i dlatego się nie pojawia.

Powód, dla którego korekty Diraca dotyczące rozwiązań Schrodinger w funkcji fali są subtelne. Wynikają z faktu, że ostatnie trzy warunki skorygowanego Hamiltoniana są podzielone przez prędkość C kwadratu, ogromną liczbę, co czyni te warunki liczbowo małe.

Może ci służyć: vy canis majoris: odkrycie, cechy, struktura, szkolenie i ewolucja

Relatywistyczne poprawki do widma energetycznego

Stosując równanie DIC-jorda, korekty występują w widmie energii elektronów w atomie wodoru. Istnieją również korekty energii w atomach z więcej niż jednym elektronem w przybliżeniu poprzez metodologię znaną jako teoria zakłóceń.

Podobnie model DIRAC pozwala znaleźć korekcję drobnej struktury na poziomie energii wodoru. 

Jednak jeszcze bardziej subtelne korekty, takie jak struktura hiperfine i przesunięcie jagnięciny, są uzyskiwane z bardziej zaawansowanych modeli, takich jak modele, takie jak Teoria kwantowa Campos, Urodzony właśnie ze względu na wkład modelu DIRAC.

Poniższy rysunek pokazuje, w jaki sposób relatywistyczne korektę Diraca są na poziomach energii:

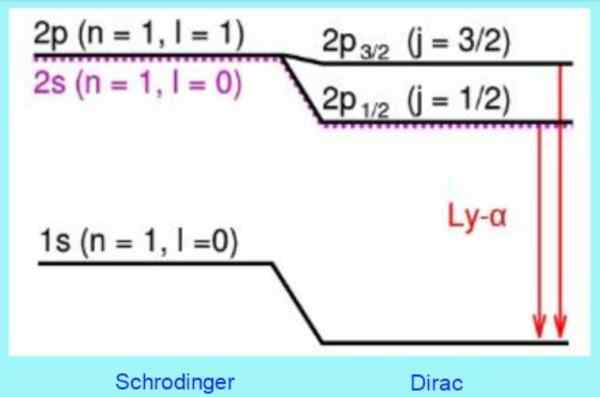Rysunek 3. Korekty modelu DIRAC na poziomach aktomu wodoru. Źródło: Wikimedia Commons.

Na przykład rozwiązania równania DIRAC prawidłowo przewidują przesunięcie obserwowane na poziomie 2s. Jest to dobrze znana korekta drobnej struktury w linii Lymana - alfa widma wodoru (patrz ryc. 3).

Nawiasem mówiąc, drobna struktura to nazwa, która odbiera w fizyce atomowej rozkładanie linii widma emisji atomów, co jest bezpośrednią konsekwencją elektronicznego spinu.

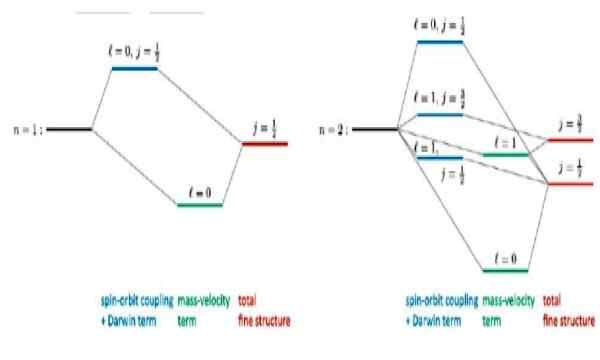Rysunek 4. Odbieranie drobnej struktury dla stanu podstawowego n = 1 i pierwszego stanu wzbudzonego n = 2 w atomie wodoru. Źródło: r Wirnata. Relatywistyczne poprawki do atomów wodorowych. Researchgate.internet

Artykuły zainteresowane

Model atomowy Broglie.

Model atomowy Chadwick.

Model atomowy Heisenberga.

Model atomowy Perrina.

Model atomowy Thomsona.

Model atomowy Dalton.

Model atomowy Schrödingera.

Model atomowy Democritus.

Model atomowy Leucipo.

Model atomowy Bohr.

Obecny model atomowy.

Bibliografia

1. Teoria atomowa. Wyzdrowiał z Wikipedii.org.
2. Moment magnetyczny elektronów. Wyzdrowiał z Wikipedii.org.
3. Quanta: Podręcznik pojęć. (1974). Oxford University Press. Wyzdrowiał z Wikipedii.org.
4. Model atomowy Dirac Jordan. Odzyskane z Prezi.com.
5. Nowy wszechświat kwantowy. Cambridge University Press. Wyzdrowiał z Wikipedii.org.