Najmniej kwadraty

Jaka jest metoda minimalnych kwadratów?

Metoda Najmniej kwadraty Jest to jedna z najważniejszych zastosowań w podejściu funkcji. Chodzi o to, aby znaleźć krzywą tak, że biorąc pod uwagę zestaw uporządkowanych par, funkcja ta lepiej podchodzi do danych. Funkcją może być linia, krzywa kwadratowa, sześcienna itp.

Ideą metody jest zminimalizowanie suma kwadratów różnic w rzędnych (składnika y), między punktami wygenerowanymi przez wybraną funkcję a punktami należącymi do zestawu danych.

Metoda minimalna kwadratowa

Przed podaniem metody musimy najpierw wyjaśnić, co „lepiej się zbliża”. Załóżmy, że poszukiwana jest linia y = b+mx, która najlepiej reprezentuje zestaw n punktów, a mianowicie (x1, y1), (x2, y2)…, (xn, yn).

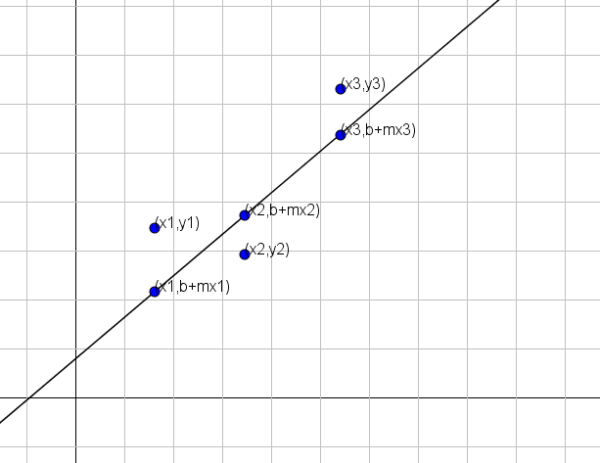
Jak pokazano na poprzednim rysunku, jeśli zmienne x i y były powiązane przez linię y = b+mx, to dla x = x1 odpowiednią wartość y wynosiłby b+mx1. Jednak ta wartość różni się od prawdziwej wartości y, czyli y = y1.

Pamiętaj, że w płaszczyźnie odległość między dwoma punktami podaje następujący wzór:

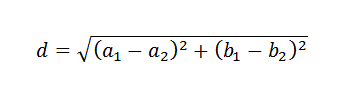
Mając to na uwadze, aby ustalić, jak wybrać linię y = b+mx, która najlepiej zbliża się do podanych danych, użycie logicznie jako kryteria wyboru linii, która minimalizuje sumę kwadratów odległości między punktami i linia.

Ponieważ odległość między punktami (x1, y1) i (x1, b+mx1) wynosi y1- (b+mx1), nasz problem jest zmniejszony do znalezienia liczb m i b, tak że następna suma jest minimalna:

Może ci służyć: zielone twierdzenie, demonstracja, aplikacje i ćwiczenia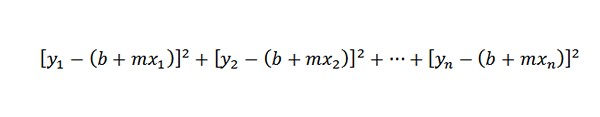

Linia spełniająca ten warunek jest znany jako „podejście do linii minimalnych kwadratów do punktów (x1, y1), (x2, y2), ..., (xn, yn)”.

Po uzyskaniu problemu pozostaje tylko metoda znalezienia podejścia przez minimalne kwadraty. Jeśli punkty (x1, y1), (x2, y2), ..., (xn, yn) są na linii y = mx+b, musielibyśmy być kolineal i:

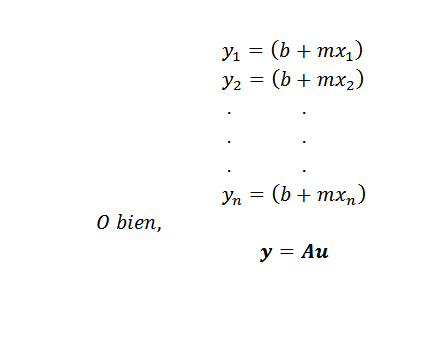
W tym wyrażeniu:

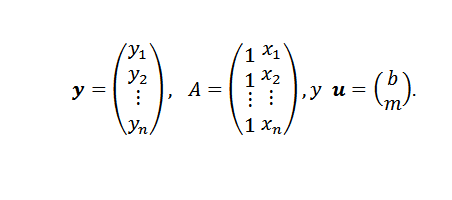
Wreszcie, jeśli punkty nie są colineal, to Y-AU = 0, a problem może przełożyć się na znalezienie wektora lub tak, że standard euklidesowy jest minimalny.

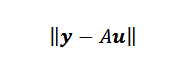
Znalezienie wektora minimalizującego lub nie jest tak trudne, jak można się wydawać. Ponieważ a ma matrycę NX2, a U to macierz 2 × 1, mamy, że wektor AU jest wektorem w R^N i należy do obrazu a, który jest podprzestrzenią r^N Z wymiarem nie więcej niż dwa.

Zakładamy, że n = 3, aby pokazać, jaka jest procedura, którą należy przestrzegać. Jeśli n = 3, obraz A będzie płaszczyzną lub linią przechodzącą przez pochodzenie.

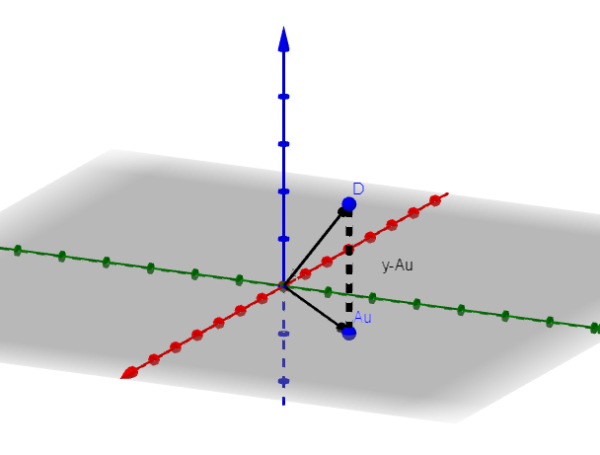
Niech v minimalizujący wektor. Na rysunku obserwujemy, że Y-AU jest zminimalizowane, gdy jest on ortogonalny do obrazu. To znaczy, jeśli v jest wektorem minimalizującym, zdarza się, że:

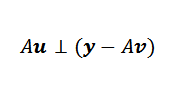
Następnie możemy wyrazić powyższe w ten sposób:

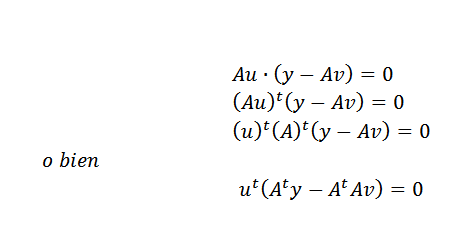
Może się to zdarzyć tylko wtedy, gdy:

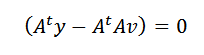
Wreszcie, oczyszczanie V, musimy:

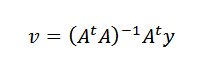
Można to zrobić^TA jest odwracalne, gdy N punkty jako dane nie są kolineal.

Teraz, jeśli zamiast szukać linii, chcemy znaleźć przypowieść (której wyrażenie byłaby formy y = a+bx+cx²) Że było to lepsze przybliżenie punktów danych, procedura zostałaby opisana poniżej.

Może ci służyć: liczby całkowitym

Gdyby punkty danych były w przypowieści, musiałoby:

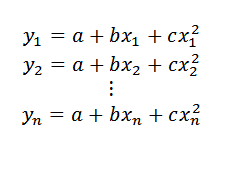
Następnie:

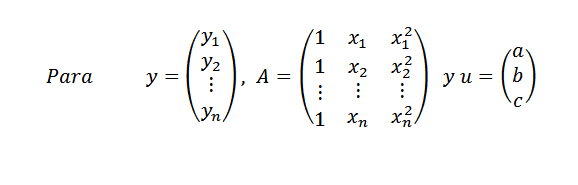
Podobnie możemy napisać y = au. Jeśli wszystkie punkty nie są w przypowieści, mamy, że Y-AU różni się od zera dla dowolnego wektora u, a naszym problemem jest ponownie: Znajdź wektor u w R3 tak, że jego norma || y-AU || być jak najwięcej.

Powtarzając poprzednią procedurę, możemy dostać się do poszukiwanego wektora:

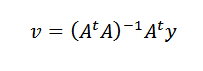
Rozwiązane ćwiczenia

Ćwiczenie 1

Znajdź linię, która najlepiej pasuje do punktów (1.4), (-2,5), (3, -1) i (4.1).

Rozwiązanie

Musimy:

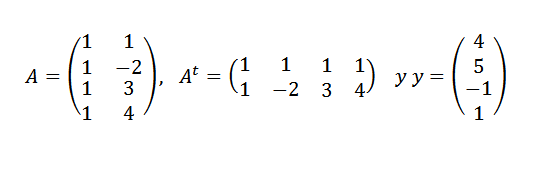
Następnie:

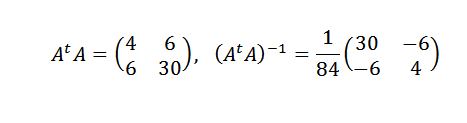
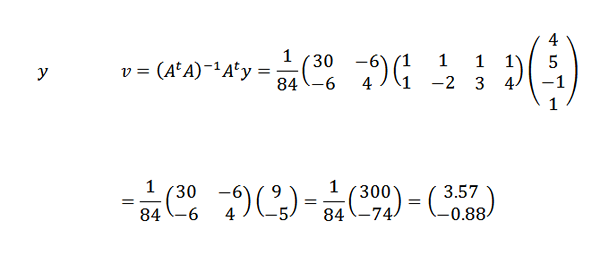
Dlatego dochodzimy do wniosku, że linia, która najlepiej odpowiada punktom, jest podana przez:

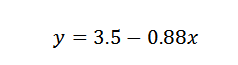
Ćwiczenie 2

Załóżmy, że obiekt jest upuszczony z wysokości 200 m. Podczas upadku podejmowane są następujące środki:

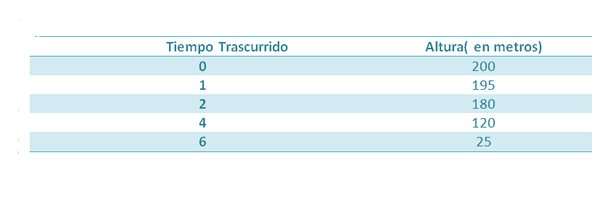
Wiemy, że wysokość tego obiektu, po upływie czasu, jest podana przez:

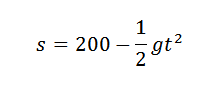
Jeśli chcemy uzyskać wartość G, możemy szukać przypowieści, która jest lepszym podejściem do pięciu punktów podanych w tabeli, a zatem mielibyśmy współczynnik towarzyszący T² Będzie to rozsądne podejście do (-1/2) g, jeśli pomiary są dokładne.

Musimy:

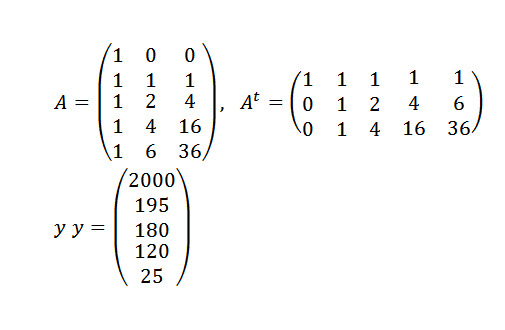
I wtedy:

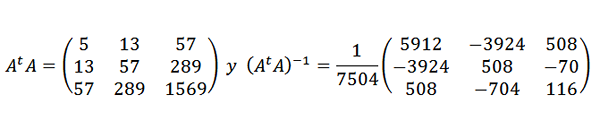
Tak więc punkty danych są dostosowywane o następujące wyrażenie kwadratowe:

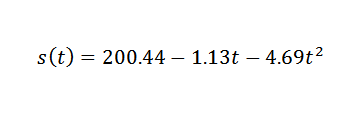
Więc musisz:

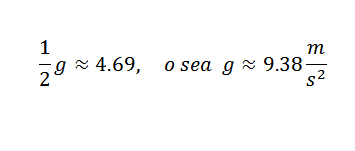
Jest to wartość, która jest dość zbliżona do prawidłowego, czyli g = 9,81 m/s². Aby uzyskać dokładniejszą g z g, konieczne byłoby rozpoczęcie od bardziej precyzyjnych obserwacji.

Jaka jest minimalna metoda kwadratowa?

W problemach, które występują w naukach przyrodniczych lub społecznych, wygodne jest pisanie relacji między różnymi zmiennymi poprzez jakąś matematyczną ekspresję.

Może ci służyć: proporcjonalna różnica

Na przykład możemy odnosić się do ekonomii koszt (c), dochód (i) i zyski (u) poprzez prostą formułę:

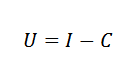
W fizyce możemy powiązać przyspieszenie spowodowane grawitacją, czasem, w którym spadał obiekt, i wysokość obiektu przez prawo:

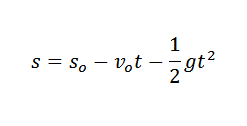
W poprzednim wyrażeniu s_albo Jest to początkowa wysokość wspomnianego obiektu i v_albo Czy Twoja początkowa prędkość.

Jednak znalezienie takich formuł nie jest prostym zadaniem; Zwykle odpowiada profesjonalistom na pracy z wieloma danymi i wielokrotnie przeprowadzając kilka eksperymentów (w celu sprawdzenia, czy uzyskane wyniki są stałe) w celu znalezienia relacji między różnymi danymi.

Częstym sposobem na osiągnięcie tego jest przedstawienie danych uzyskanych w płaszczyźnie jako punktów i poszukiwanie funkcji ciągłej, która optymalnie zbliża się do tych punktów.

Jednym ze sposobów znalezienia funkcji, która „lepsza podejście”, podane dane, jest metoda minimum kwadratowych.

Ponadto, jak widzieliśmy również w ćwiczeniu, dzięki tej metodzie możemy osiągnąć dość bliskie podejścia do stałych fizycznych.