Przybliżony pomiar amorficznych liczb przykładowych i ćwiczeń

Przybliżony pomiar Figur amorficznych składa się z szeregu metod zastosowanych do określenia obszaru lub obwodu liczb geometrycznych, które nie są trójkąty, kwadraty, kółka itp. Niektóre są rozszerzalne do trzech wymiarów figur.

Zasadniczo pomiar polega na regularnym tworzeniu siatków, takich jak prostokąty, kwadraty lub trapezoidy, które pokrywają w przybliżeniu powierzchnię. Dokładność podejścia obszaru uzyskanego przez te metody wzrasta wraz z finezją lub gęstością siatkowania.

Rysunek 1. Kamienie w kształcie amorficznych postaci. Źródło: pxfuel.

Ryciny 1 i 2 pokazują różne amorficzne postacie. Aby obliczyć obszar, siatkówki, złożone z 2 x 2 kwadratu, które z kolei są podzielone na dwadzieścia pięć kwadratów 2/5 x 2/5.

Dodanie obszarów głównych kwadratów i kwadratów wtórnych uzyskuje się przybliżony obszar liczby amorficznej.

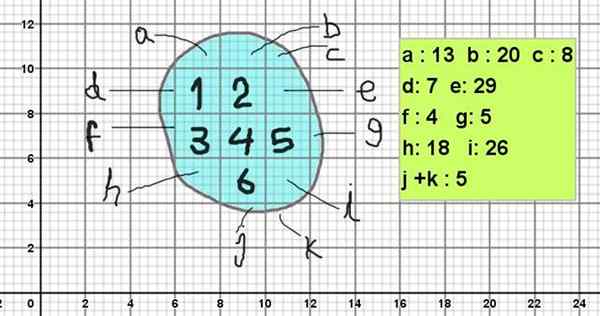
Rysunek 2. Siatkowy do obliczenia obszaru jednej z amorficznych postaci w przybliżony sposób. Źródło: f. Zapata

[TOC]

Obszar pod krzywą

Często konieczne jest obliczenie obszaru pod krzywą między dwoma wartościami granicznymi. W tym przypadku zamiast kwadratowego siatkowania, prostokątne paski można prześledzić w przybliżeniu obszar pod wspomnianą krzywą.

Suma wszystkich prostokątnych pasków nazywana jest Suma lub suma Riemanna. Rysunek 3 pokazuje partycję przedziału [a, b], na której chcesz określić w przybliżeniu obszar pod krzywą.

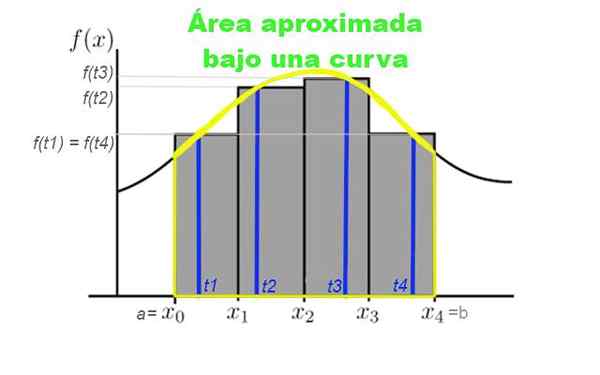Rysunek 3. Podział interwału [a, b] w czterech podinterwachach, które zwykle są pobierane z tej samej szerokości. Wysokość prostokątów zależy od wartości krzywej dla TK należącego do podinterwali. Źródło: f. Zapata.

Załóżmy, że chcesz obliczyć obszar pod krzywą podaną przez funkcję y = f (x), gdzie x należy do interwału [a, b], w którym chcesz obliczyć obszar. W tym celu powstaje partycja N elementów w tym przedziale:

Może ci służyć: 60 dzielników

Parition = x0 = a, x1, x2, ..., xn = b.

Następnie przybliżony obszar pod krzywą podaną przez y = f (x) w przedziale [a, b] osiąga się przez następującą sumę:

S = ∑_{K = 1}^N f (t_k) (X_k - X_K-1)

Gdzie t_k jest między x_K-1 i x_k: X_K-1 ≤ t_k ≤ x_k .

Rysunek 3 pokazuje sumę riemann krzywej y = f (x) w przedziale [x0, x4]. W tym przypadku wykonano partycję czterech podinterwali, a suma reprezentuje całkowity obszar szarych prostokątów. 

Ta suma reprezentuje podejście do obszaru pod krzywą F między odciętymi x = x0 i x = x4.

Podejście do obszaru pod krzywą poprawia się w zakresie, w jakim liczba N partycji jest większa i zwykle jest to obszar pod krzywą, gdy liczba N partycje mają tendencję do nieskończoności. 

W przypadku, gdy krzywa jest reprezentowana przez funkcję analityczną, wartości f (t_k) Są one obliczane oceniając wspomnianą funkcję w wartościach t_k. Ale jeśli krzywa nie ma wyrażenia analitycznego, pozostają następujące możliwości:

1. Podejdź do krzywej przez funkcję, na przykład wielomian.
2. Weź udział w kartezjańskich współrzędnych punktów, w których krzywa jest przechwytywana z liniami x = t_k.

Regularne odstępy

W zależności od wyboru wartości TK w przedziale [x_k, X_K-1], suma może przecenić lub nie docenić dokładnej wartości obszaru pod krzywą funkcji y = f (x). Najbardziej wskazaną rzeczą jest przejęcie punktu TK, w którym brakujący obszar jest w przybliżeniu równy pozostałemu obszarowi, chociaż nie zawsze możliwe jest dokonanie takiego wyboru.  

Może ci służyć: odwrotność multiplikatywna: wyjaśnienie, przykłady, rozwiązane ćwiczenia

Weź TK na końcu

Najbardziej praktyczną rzeczą jest zatem stosowanie regularnych interwałów szerokich δx = (b - a)/n, gdzie a i b są minimalnymi i maksymalnymi wartościami odciętej, a n jest liczbą poddziałów.

W takim przypadku obszar pod krzywą zbliża się do:

Obszar = f (a+δx)+f (a+2Δx)+…+f [a+(n-1] δx+f (b)*δx

W poprzednim wyrażeniu TK wzięto na prawym końcu podinterwale.

Weź TK na lewym końcu

Inną praktyczną możliwością jest przyjęcie wartości TK na lewym końcu, w którym to przypadku suma, która przybliża obszar, jest wyrażona jako:

Obszar = [f (a)+f (a+δx)+…+f (a+(n-1) δx)*δx

TK jako wartość centralna

W przypadku wybierania TK jako centralnej wartości zwykłej podinterval szerokości δx, suma zbliżona do obszaru pod krzywą jest:

Obszar = [f (a+δx/2)+f (a+3Δx/2)+…+f (b-δx/2)]*δx

Każdy z tych wyrażeń ma tendencję do dokładnej wartości w zakresie, w jakim liczba podziałów jest arbitralnie duża, to znaczy, że δx ma tendencję do zera, ale w tym przypadku liczba warunków suma jest niezwykle duża z wynikającymi z tego kosztu obliczeniowego kosztu obliczeniowego. 

Przykład

Ryc. 2 pokazuje figurę amorficzną, której kontur jest podobny do kamieni obrazu 1. Aby obliczyć jego powierzchnię, jest on umieszczany na siatkowym z głównymi kwadratami 2 x 2 jednostkami do kwadratu (na przykład mogą wynosić 2 cm²).

A ponieważ każdy kwadrat jest podzielony na poddziały 5 x 5, każde podział ma powierzchnię 0,4 x 0,4 jednostek kwadratowych (0,16 cm²).

Rysunek na rysunku zostanie obliczony w następujący sposób:

Może ci służyć: wspólna faktoryzacja: przykłady i ćwiczenia

Obszar = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

To jest do powiedzenia:

Obszar = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Ćwiczenie rozwiązane

Oblicz w przybliżeniu obszar pod krzywą podaną przez funkcję f (x) = x² Bet a = -2 do b = +2. Aby to zrobić, napisz sumę n regularnych partycji przedziału [a, b], a następnie weź limit matematyczny dla przypadków, że liczba partycji ma tendencję do nieskończoności. 

Rozwiązanie

Po pierwsze, przedział partycji jest zdefiniowany jako 

Δx = (B - a)/n. 

Następnie suma dla prawej odpowiadającej funkcji f (x) jest taka:

A = -2 i b =+2 są zastąpione, aby przedział lub krok wynosił δx = 4/n. W takim przypadku suma funkcji f (x) = x² Jest:

 Opracowywany jest kwadratowy dwumian: 

[-2 +(4i/n)]² = 4 - 16 I /N + (4 /n)² Siema²

A następnie zostaje zastąpiony w sumie:

Uzyskuje się oddzielenie podsumowań i przyjmowanie stałych ilości jako wspólnego współczynnika każdej sumy:

 Pierwsza suma, druga to:

A trzeci to:

Zastąpienie wyrażenia posiadanej sumy:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Wybierając dużą wartość dla n, masz dobre podejście do obszaru pod krzywą. Jednak w tym przypadku możliwe jest osiągnięcie dokładnej wartości przenoszącym limit matematyczny, gdy n ma tendencję do nieskończoności:

Obszar = lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6N²]

Obszar = 16 - (64/2)+ (64/3) = 16/3 = 5,333.

Bibliografia

1. Casteleiro, J. M. 2002. Kompleksowe obliczenia (wydanie ilustrowane). Madryt: ESIC Editorial.
2. Larson, r. 2010. Obliczanie zmiennej. 9na. Wydanie. McGraw Hill.
3. Purcell, e. 2007. Obliczanie za pomocą geometrii analitycznej. 9na. Wydanie. Edukacja Pearsona.
4. Unican. Historia koncepcji integralnej. Odzyskane z: repozytorium.Unican.Jest
5. UIS. Riemann Sums. Odzyskane z: matematyki.UIS.Edu.współ
6. Wikipedia. Obszar. Odzyskane z: jest.Wikipedia.com