Wielkość wektora

Jaka jest wielkość wektorowa?

A Wielkość wektora Jest to każde wyrażenie reprezentowane przez wektor, który ma wartość numeryczną (moduł), kierunek, kierunek i punkt zastosowania. Niektóre przykłady wielkości wektorowych to przemieszczenie, prędkość, wytrzymałość i pole elektryczne.

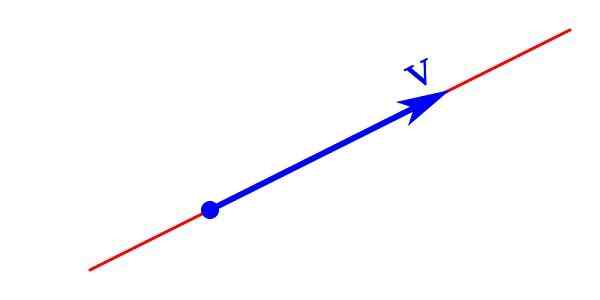
Graficzna reprezentacja wielkości wektorowej składa się ze strzałki, której końcówka wskazuje na jej kierunek i kierunek, jego długość jest modułem, a punktem początkowym jest pochodzenie lub punkt zastosowania.

Graficzna reprezentacja wektora

Wielkość wektora jest reprezentowana analitycznie z literą, która przenosi strzałkę na szczycie prawej strony w kierunku poziomym. Może być również reprezentowany listem napisanym odważnym V którego moduł ǀVǀ Jest napisane kursywą V.

Jednym z zastosowań pojęcia wielkości wektora jest projektowanie autostrad i dróg, szczególnie w projektowaniu jej krzywizny. Inną aplikacją jest obliczenie przemieszczenia między dwoma miejscami lub zmiana prędkości pojazdu.

Elementy wielkości wektorowej

Wielkość wektora jest dowolną jednostką reprezentowaną przez segment linii, z orientacją w przestrzeni, która ma charakterystykę wektora. Jego elementy to:

Moduł: Jest to wartość liczbowa wskazująca wielkość lub intensywność wielkości wektora.

Adres: To orientacja segmentu linii w zawierającej go przestrzeni. Wektor może mieć kierunek poziome, pionowe lub pochylone; Północ, południe, ten lub zachód; Północno -wschodni, południowo -wschodni, południowy lub północno -zachodni.

Sens: Jest to wskazane końcówką strzałki na końcu wektora.

Może ci służyć: fizyka przed Greków (Antigua Grecja)

Punkt aplikacji: Jest to pochodzenie lub punkt początkowego działania wektora.

Klasyfikacja wektorowa

Wektory są klasyfikowane jako kolinearne, równoległe, prostopadłe, współbieżne, kuplety, bezpłatne, przesuwane, przeciwnie, sprzęt, stały i jednostkowy.

Colineal: Należą lub działają na tej samej linii prostej, są również nazywane zależne od linii I mogą być pionowe, poziome i nachylone.

Parallele: Mają ten sam adres lub skłonność.

Prostopadły: Dwa wektory są prostopadłe do siebie, gdy kąt między nimi wynosi 90 °.

Równoległy: Są wektorami, które przesuwając się nad linią akcji, zbiegają się w tym samym punkcie w kosmosie.

Coplanarios: Działają w płaszczyźnie, na przykład samolot Xy.

Bezpłatny: Poruszają się w dowolnym miejscu w przestrzeni, zachowując swój moduł, kierunek i znaczenie.

Slajd: Poruszają się wzdłuż linii działania określonego przez ich kierunek.

Przeciwieństwa: Mają ten sam moduł i kierunek oraz przeciwny kierunek.

Sprzęt: Mają ten sam moduł, kierunek i znaczenie.

Naprawił: Punkt aplikacji ma niezmienne.

Unitary: Wektory, których modułem jest jednostka.

Komponenty wektorowe

Wielkość wektora w trójwymiarowej przestrzeni jest reprezentowana w układzie trzech osi prostopadłych do siebie (X i Z) Orthogonal wypróbował.

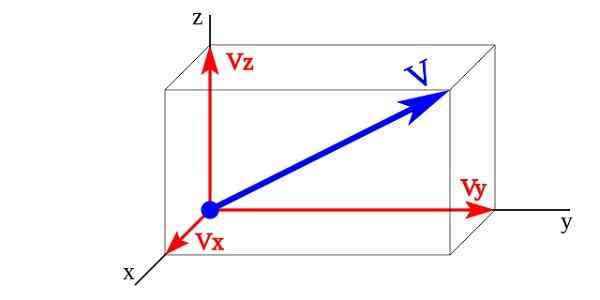Składniki wektorowe o wielkości wektorowej

Na obrazie wektory VX, Vy, VZ to elementy wektorowe wektorowe V których wektory jednostkowe są X,I,z. Wielkość wektora V Jest reprezentowany przez sumę komponentów wektorowych.

V = Vx + Vy + VZ

Wynikiem kilku wielkości wektorowych jest suma wektorowa wszystkich wektorów i zastępuje te wektory w układzie.

Pole wektorowe

Pole wektorowe jest regionem przestrzeni, w której w każdym z jego punktów odpowiada wielkości wektora. Jeśli objawiająca się wielkość jest siłą działającą na ciało lub układ fizyczny, pole wektorowe jest polem sił.

Może ci służyć: Twierdzenie Steiner: Wyjaśnienie, aplikacje, ćwiczenia

Pole wektorowe jest reprezentowane graficznie przez linie pola, które są styczną linii wielkości wektora we wszystkich punktach w regionie. Niektóre przykłady pól wektorowych to pole elektryczne utworzone przez punktualny ładunek elektryczny w polu przestrzeni i prędkości płynu.

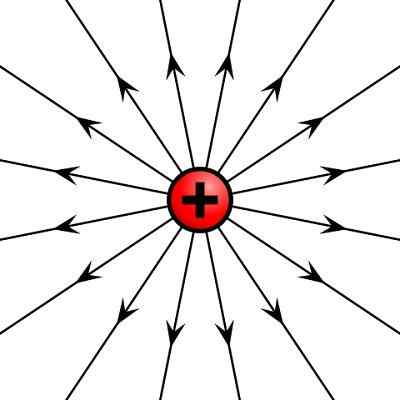Pole elektryczne utworzone przez dodatni ładunek elektryczny

Operacje z wektorami

Dodanie wektorów: Jest to wynik dwóch lub więcej wektorów. Jeśli masz dwa wektory ALBO I P Suma jest ALBO + P = q. Wektor Q Jest to wynikowy wektor, który jest uzyskiwany graficznie poruszający pochodzenie wektora DO do końca wektora B.

Odejmowanie wektora: Odejmowanie dwóch wektorów lub i P Jest ALBO - P = Q. Wektor Q  Dostajesz dodanie do wektora ALBO Twój przeciwieństwo -P. Metoda graficzna jest taka sama jak suma z różnicą, że wektor przeciwny jest przenoszony.

Produkt skalarny: Iloczyn wielkości skalarnej Do przez wielkość wektora P To wektor poseł który ma ten sam kierunek wektora P. Jeśli wielkość skalarna wynosi zero, produkt skalarny jest wektorem zerowym.

Przykłady wielkości wektora

Pozycja

Położenie obiektu lub cząstki w odniesieniu do układu odniesienia jest wektorem podawanym przez jego prostokątne współrzędne X i Z, i jest reprezentowany przez komponenty wektorowe Xî, Yĵ, ZK. Wektory  Siema, J, k Są wektorami jednostkowymi.

Cząsteczka w pewnym momencie (X i Z) ma wektor pozycji R = Xî + Yĵ + ZK. Wartość liczbowa pozycji wektorowej wynosi R= √ (X² + I² + z²). Zmiana pozycji cząstek z jednej pozycji na drugą w odniesieniu do systemu odniesienia jest wektor Przemieszczenie δR I jest obliczane na następującym wyrażeniu wektora:

Może ci służyć: promienie anodowe

ΔR = r₂ - R₁

Przyśpieszenie

Średnie przyspieszenie (Do_M) Jest zdefiniowany jako zmienność prędkości v W przedziale czasowym Δt A wyrażenie do obliczenia jest Do_M= Δv/δt, istnienie Δv Prędkość zmiany wektora.

Natychmiastowe przyspieszenie (Do) to granica średniego przyspieszenia Do_M Kiedy Δt staje się tak mały, że ma tendencję do zera. Natychmiastowe przyspieszenie jest wyrażone zgodnie z jego komponentami wektorowymi

Do =Do_XSiema +Do_I J+ Do_zk

Pole grawitacyjne

Siła przyciągania grawitacyjna wywierana przez masę M, Położony u pochodzenia, na innej masie M W pewnym momencie w kosmosie X, I, z Jest to pole wektorowe zwane pole sił grawitacyjnych. Siła ta jest podana przez wyrażenie:

F= (-mmg/R)ȓ

R = Xî + Yĵ + ZK

F = Jest to siła grawitacyjna wielkości fizycznej

G = jest uniwersalną stałą grawitacji

ȓ = jest wektorem pozycji masowej M

Bibliografia

1. Tallack, J C. Wprowadzenie do analizy wektorowej. Cambridge: Cambridge University Press, 2009.
2. Spiegel, M R, Lipschutz, S i Spellman, D. Wektor analizy. S.L. : MC Graw Hill, 2009.
3. Marka, l. Wektor analizy. New York: Dover Publications, 2006.
4. Griffiths, D J. Wprowadzenie do elektrodynamiki. New Jersey: Prentice Hall, 1999. P. 1-10.
5. Haga, ur. Wprowadzenie do analizy wektorowej. Glasgow: Methuen & Co. Ltd, 2012.