Algebra wektorowa

Jaka jest algebra wektorowa?

On Algebra wektorowa Jest to gałąź matematyki odpowiedzialna za badanie systemów równań liniowych, wektorów, macierzy, przestrzeni wektorowych i ich transformacji liniowych. Jest to związane z takimi obszarami, jak inżynieria, rozwiązywanie równań różniczkowych, analiza funkcjonalna, badania operacyjne, grafika obliczeniowa,.

Innym z obszarów, które przyjęła algebra liniowa, jest fizyka, ponieważ dzięki temu można było opracować badanie zjawisk fizycznych, opisując je za pomocą wektorów. To umożliwiło lepsze zrozumienie wszechświata.

Podstawy

Algebra wektorowa pochodzi z badania czwartorzędowych (rozszerzenie liczb rzeczywistych) 1, I, J i K, a także geometrii kartezjańskiej promowanej przez Gibbsa i Heaviside, który zdał sobie sprawę, że wektory będą służyć jako instrument reprezentowania kilka zjawisk fizycznych.

Algebra wektorowa jest badana przez trzy fundamenty:

Geometrycznie

Wektory są reprezentowane przez linie, które mają orientację, a operacje takie jak suma, odejmowanie i mnożenie przez liczby rzeczywiste są zdefiniowane metodami geometrycznymi.

Analitycznie

Opis wektorów i ich działalności odbywa się za pomocą liczb, zwanych komponentami. Ten typ opisu jest wynikiem reprezentacji geometrycznej, ponieważ używany jest układ współrzędnych.

Aksjomatycznie

Opis wektorów jest wykonany, niezależnie od układu współrzędnych lub dowolnego rodzaju reprezentacji geometrycznej.

Badanie liczb w przestrzeni odbywa się poprzez jego reprezentację w systemie referencyjnym, który może znajdować się w jednym lub więcej wymiarach. Wśród głównych systemów są:

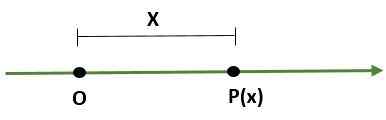
• Układ jednoznaczny, że jest to linia, w której punkt (lub) reprezentuje pochodzenie, a inny punkt (p) określa skalę (długość) i kierunek tego:

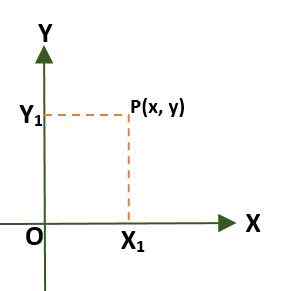
• Prostokątny układ współrzędnych (dwukierunkowy), który składa się z dwóch prostopadłych linii zwanych oś x i y, które przechodzą przez pochodzenie punktu (lub); W ten sposób plan jest podzielony na cztery regiony zwane kwadrantami. W tym przypadku punkt (p) w płaszczyźnie jest podany przez odległości między osiami a P.

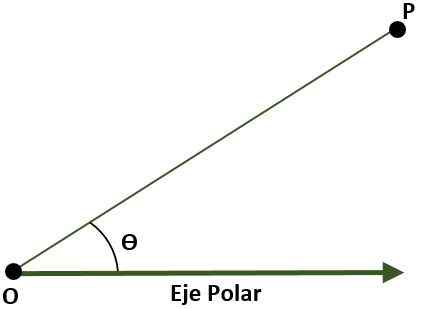
• Układ współrzędnych polarnych (dwukierunkowy). W takim przypadku system składa się z punktu O (pochodzenia), który nazywa się słupem i półiver. W tym przypadku punkt P płaszczyzny, w odniesieniu do bieguna i osi polarnej, jest podany przez kąt (ɵ), który jest utworzony przez odległość między pochodzeniem a punktem p.

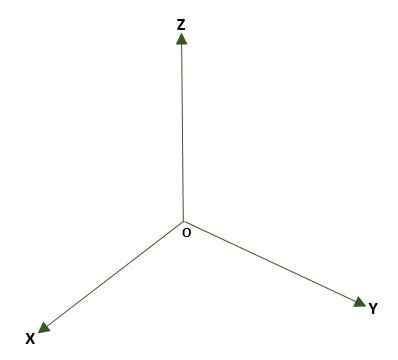
• Prostokątny trójwymiarowy układ, utworzone przez trzy prostopadłe linie (x, y, z), które mają jako punkt lub w przestrzeni. Powstają trzy samoloty współrzędne: XY, XZ i YZ; Przestrzeń zostanie podzielona na osiem regionów zwanych oktantami. Odniesienie punktu P przestrzeni są podawane przez odległości między samolotami a P.

Wielkości

Wielkość jest ilością fizyczną, którą można policzyć lub mierzyć za pomocą wartości numerycznej, jak w przypadku niektórych zjawisk fizycznych; Jednak często konieczne jest opisanie tych zjawisk z innymi czynnikami, które nie są numeryczne. Dlatego wielkości są podzielone na dwa typy:

Wielkość skalarna

Są to kwoty, które są zdefiniowane i reprezentowane w sposób numeryczny; to znaczy przez moduł wraz z jednostką miary. Na przykład:

a) Czas: 5 sekund.

b) Masa: 10 kg.

c) Tom: 40 ml.

D) Temperatura: 40 ° C.

Wielkość wektora

Są to kwoty, które są zdefiniowane i reprezentowane przez moduł wraz z jednostką, a także przez sens i kierunek. Na przykład:

Może ci służyć: symbolizacja wyrażeń

a) prędkość: (5ȋ - 3ĵ) m/s.

b) Przyspieszenie: 13 m /s²; S 45º e.

c) Siła: 280 N, 120º.

d) waga: -40 ĵ kg -f.

Wielkości wektorowe są reprezentowane graficznie przez wektory.

Co to są wektory?

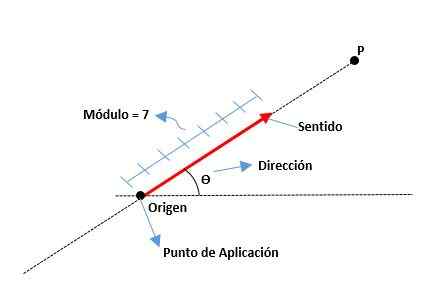
Wektory to graficzne reprezentacje wielkości wektora; to znaczy są segmentami linii, w których jego ostatni koniec jest wierzchołkiem strzałki.

Są one określone przez moduł lub długość segmentu, ich sens wskazany przez czubek strzałki i kierunek zgodnie z linią, do której należy. Pochodzenie wektora jest również znane jako punkt zastosowania.

Elementy wektora są następujące:

Moduł

Jest to odległość od pochodzenia do końca wektora, reprezentowanego przez liczbę rzeczywistą wraz z jednostką. Na przykład:

| OM | = | A | = A = 6 cm

Adres

Jest to miara kąta, która istnieje między osą x (z dodatnim) a wektorem, a także punktami kardynał (północ, południe, wschód i zachód).

Sens

Jest podawany przez końcówkę strzałki znajdującej się na końcu wektora, wskazując, gdzie jest to kierowane.

Klasyfikacja wektorów

Zasadniczo wektory są klasyfikowane jako:

Stały wektor

To ten, którego punkt aplikacji (pochodzenie) jest ustalony; Oznacza to, że pozostaje powiązany z przestrzenią przestrzeni, więc nie może się w tym poruszać.

Wolny wektor

Może swobodnie poruszać się w przestrzeni, ponieważ jego pochodzenie porusza się do dowolnego punktu bez zmiany modułu, znaczenia lub kierunku.

Przesuwany wektor

Jest to taki, który może przenieść swoje pochodzenie wzdłuż linii działania bez zmiany modułu, znaczenia lub kierunku.

Właściwości wektorowe

Wśród głównych właściwości wektorów są następujące:

Equipocent wektory

Są to wolne wektory, które mają ten sam moduł, kierunek (lub są równoległe) i sensowne jako wektor przesuwny lub stały wektor.

Równoważne wektory

Występuje, gdy dwa wektory mają ten sam adres (lub są równoległe), ten sam sens i pomimo różnych modułów i punktów zastosowania, powodują równe efekty.

Równość wektorowa

Mają one ten sam moduł, kierunek i sens, nawet gdy ich punkty początkowe są różne, co pozwala wektorowi równoległego do siebie bez wpływu.

Przeciwne wektory

Są tymi, którzy mają ten sam moduł i kierunek, ale ich znaczenie jest odwrotne.

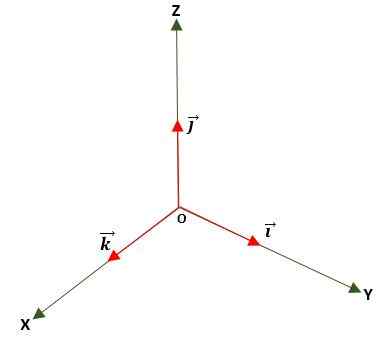
Jednostki wektor

Jest to taki, w którym moduł jest równy jednostce (1). Uzyskuje się to przez podzielenie wektora przez jego moduł i służy do określenia kierunku i kierunku wektora, w płaszczyźnie lub w przestrzeni, przy użyciu znormalizowanych wektorów podstawowych lub jednostkowych, które są:

Wektor zerowy

To ten, którego moduł jest równy 0; to znaczy jego punkt pochodzenia i ekstremalne pokrywa się w tym samym momencie.

Komponenty wektorowe

Składniki wektora to te wartości projekcji wektora na osiach systemu odniesienia; W zależności od rozkładu wektora, który może znajdować się w osiach dwóch lub trzech wymiarów, zostaną uzyskane odpowiednio dwa lub trzy składniki.

Składniki wektora są liczbami rzeczywistymi, które mogą być dodatnie, ujemne lub nawet zero (0).

W ten sposób, jeśli masz wektor ā, pochodzący z prostokątnego układu współrzędnych w płaszczyźnie xy (dwukenowe), projekcja na osi x wynosi āx, a projekcja na osi y i jest aryy. Zatem wektor zostanie wyrażony jako suma wektorów składowych.

Przykłady

Pierwszy przykład

Masz wektor ā, który zaczyna się od pochodzenia i podano współrzędne jego końców. Zatem wektor ā = (ā_X; DO_I) = (4; 5) cm.

Może ci służyć: 120 dzielników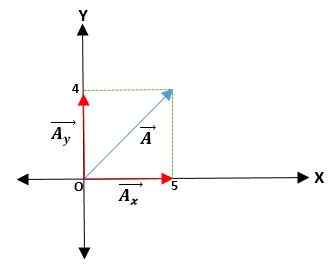

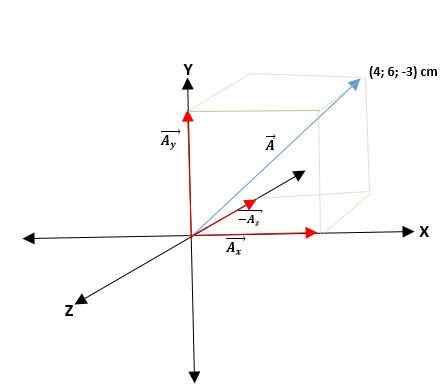
Jeżeli wektor ā działa na początek trójwymiarowego trójkątnego układu współrzędnych (w przestrzeni) x, y, z, do innego punktu (p), projekcje na ich osiach będą ary, āy i āz; Zatem wektor zostanie wyrażony jako suma trzech wektorów składowych.

Drugi przykład

Masz wektor ā, który zaczyna się od pochodzenia i podano współrzędne jego końców. Zatem wektor ā = (a_X; DO_I; DO_z) = (4; 6; -3) cm.

Wektory, które mają swoje prostokątne współrzędne, można wyrazić zgodnie z ich wektorami podstawowymi. W tym celu tylko każda współrzędna musi być pomnożona przez odpowiedni wektor jednostkowy, aby dla płaszczyzny i przestrzeni były następujące:

Dla płaszczyzny: ā = a_XI +a_IJ.

Dla przestrzeni: ā = a_XI +a_IJ+a_zk.

Operacje z wektorami

Istnieje wiele wielkości, które mają moduł, znaczenie i kierunek, takie jak przyspieszenie, prędkość, przemieszczenie, siła,.

Są one stosowane w różnych obszarach nauki i aby je zastosować, w niektórych przypadkach konieczne jest wykonywanie operacji, takich jak suma, odejmowanie, mnożenie i podział wektorów i skalarów.

dodanie i odejmowanie wektorów

Suma i odejmowanie wektorów są uważane za pojedynczą operację algebraiczną, ponieważ odejmowanie można zapisać jako sumę; Na przykład odejmowanie wektorów ā i ē można wyrazić jako:

Ā - ē = ā + (-laz)

Istnieją różne metody wykonywania sumy i odejmowania wektorów: mogą to być grafika lub analizy.

Metody graficzne

Używane, gdy wektor ma moduł, sens i kierunek. W tym celu rysowane są linie, które tworzą liczbę, która następnie pomaga określić powstały. Wśród najbardziej znanych są następujące:

Metoda równoległobramowa

Aby suma lub odejmowanie dwóch wektorów wybierany jest wspólny punkt na osi współrzędnej -który będzie reprezentował punkt pochodzenia wektorów -utrzymując ich moduł, kierunek i kierunek.

Następnie linie równoległe są rysowane do wektorów, aby utworzyć równoległobok. Powstały wektor to przekątna, która odchodzi od punktu pochodzenia obu wektorów do wierzchołka równoległoboku:

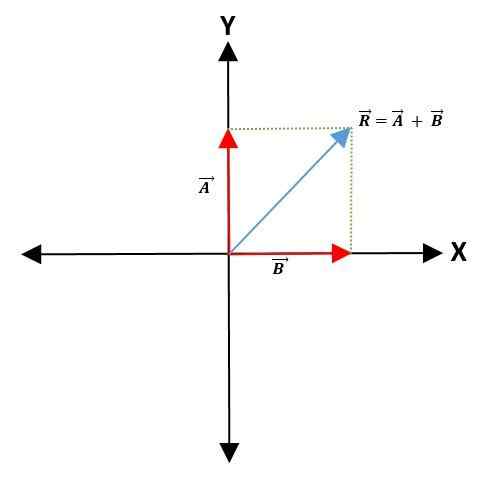
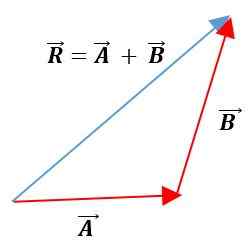
Metoda trójkąta

W tej metodzie wektory są umieszczane poniżej drugiego, utrzymując swoje moduły, zmysły i adresy. Powstały wektor będzie związkiem pochodzenia pierwszego wektora z końcem drugiego wektora:

Metody analityczne

Dwa lub więcej wektorów można dodać lub odejmować metodą geometryczną lub wektorową:

Metoda geometryczna

Gdy dwa wektory tworzą trójkąt lub równoległobok, M [Odulo i kierunek powstałego wektora można określić za pomocą praw piersi i cosinus. Zatem wynikowy moduł wektorowy, stosując prawo cosinusa i metodą trójkąta, jest podany przez:

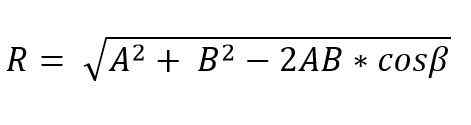
W tym wzorze β jest odwrotny kąt od strony R, a to jest równe 180º - ɵ.

Z drugiej strony metodą równoległoboku powstały moduł wektorowy:

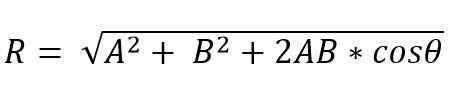
Powstały adres wektorowy jest podany przez kąt (α), który tworzy wynikowy z jednym z wektorów.

Zgodnie z prawem piersi suma lub odejmowanie wektorów można również wykonać metodą trójkąta lub równoległoboku, wiedząc, że w każdym trójkącie boki są proporcjonalne do piersi przystojnych kątów:

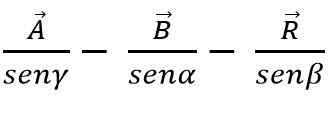
Metoda wektora

Można to zrobić na dwa sposoby: w zależności od jego prostokątnych współrzędnych lub wektorów podstawowych.

Wektory, które zostaną dodane lub odejmowane w kierunku pochodzenia współrzędnych, można wykonać, a następnie wszystkie projekcje są podzielone na ich prostokątne składniki w każdej osie płaszczyzny (x, y) lub przestrzeni (x, x, i z); Wreszcie, jego komponenty są dodawane algebraicznie. Tak więc dla samolotu jest to:

Może ci służyć: liczby Primo: Charakterystyka, przykłady, ćwiczenia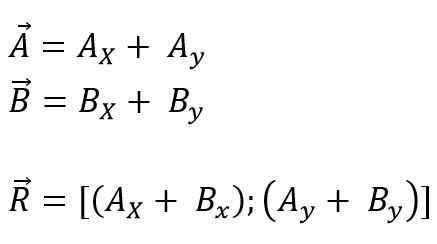

Powstały moduł wektorowy to:

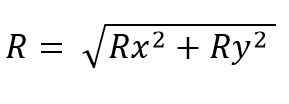
Podczas gdy dla przestrzeni jest to:

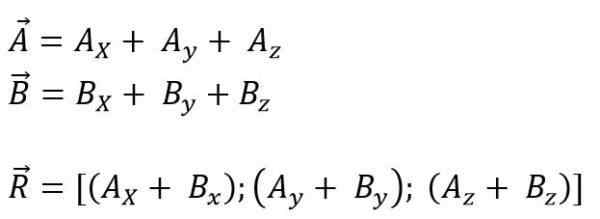
Powstały moduł wektorowy to:

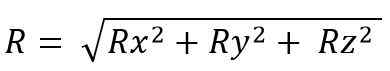
Po przeprowadzaniu sum wektorowych stosowanych jest kilka nieruchomości, które są:

• Łączność: Wynik nie zmienia się, najpierw dodając dwa wektory, a następnie dodając trzeci wektor.
• Własność przemienna: Kolejność wektorów nie zmienia wynikowych.
• Wektor nieruchomości dystrybucyjne: Jeśli skalar jest mnożony przez sumę dwóch wektorów, jest on równy mnożeniem skalarnego dla każdego wektora.
• Dystrybucyjny skalar nieruchomości: Jeśli wektor jest mnożony przez sumę dwóch skalarów, jest on równy mnożeniem wektora dla każdego skalarnego.

Mnożenie wektorowe

Mnożenie lub produkt wektorów można przeprowadzić jako sumę lub odejmowanie, ale czyniąc to, traci znaczenie fizyczne i prawie nigdy nie znajduje się w aplikacjach. Dlatego ogólnie najczęściej używanymi rodzajami produktów są produkt skalarny i wektorowy.

Produkt skalarny

Jest również znany jako punkt dwóch wektorów. Gdy moduły dwóch wektorów są pomnożone przez uformowane między nimi cosinus o mniejszym kątu, uzyskuje się skalar. Aby wyrazić produkt skalarny między dwoma wektorami, umieszcza się między nimi punkt, co można zdefiniować jako:

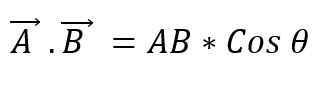
Wartość kąta, który między dwoma wektorami będzie zależeć od tego, czy są one równoległe czy prostopadłe; Zatem musisz:

• Jeśli wektory są równoległe i mają ten sam sens, Coseno 0º = 1.
• Jeśli wektory są równoległe i mają przeciwne zmysły, Coseno 180º = -1.
• Jeśli wektory są prostopadłe, Coseno 90º = 0.

Ten kąt można również obliczyć, wiedząc, że:

Produkt skalarny ma następujące właściwości:

• Własność przemienna: Zakon wektorów nie zmienia skalar.
• Własność dystrybucyjna: Jeśli skalar jest mnożony przez sumę dwóch wektorów, jest ona równa mnożeniem skalarnego dla każdego wektora.

Produkt wektorowy

Mnożenie wektorowe lub produkt krzyżowy dwóch wektorów A i B, spowoduje nowy wektor C i wyraża przy użyciu krzyża między wektorami:

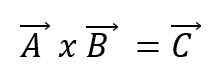
Nowy wektor będzie miał swoją własne cechy. W ten sposób:

• adres: Ten nowy wektor będzie prostopadły do ​​płaszczyzny, który jest określony przez oryginalne wektory.
• On sens: Wynika to z zasadą prawej ręki, w której wektor a jest obracany do b, wskazując kierunek obrotu palcami, a kciukiem jest zaznaczony kierunek wektora.
• On moduł: Określa się to przez mnożenie modułów wektorów AXB, przez piersią niewielki kąt, który między tymi wektorami. Jest wyrażony:

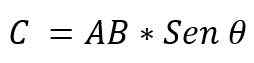
Wartość kąta, która istnieje między dwoma wektorami, będzie zależeć od tego, czy są one równoległe czy prostopadłe. Tak więc możliwe jest potwierdzenie następujących:

• Jeśli wektory są równoległe i mają to samo znaczenie, sine 0º = 0.
• Jeśli wektory są równoległe i mają przeciwne zmysły, sinus 180º = 0.
• Jeśli wektory są prostopadłe, sine 90º = 1.

Gdy produkt wektorowy jest wyrażany zgodnie z jego wektorami podstawowymi, musi:

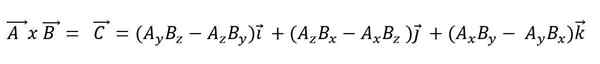
Produkt skalarny ma następujące właściwości:

• To nie jest do pracy: kolejność wektorów zmienia skalar.
• Własność dystrybucyjna: Jeśli skalar jest mnożony przez sumę dwóch wektorów, jest ona równa mnożeniem skalarnego dla każdego wektora.