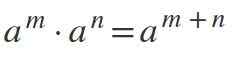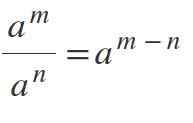Prawa wykładników

Jakie są prawa wykładników?

Prawa wykładników Są to te, które mają zastosowanie do tej liczby, która wskazuje, ile razy liczba podstawowa musi zostać pomnożona sama w sobie. Wykładniki są również znane jako moce. Potęgowanie jest operacją matematyczną utworzoną przez podstawę (a), wykładnik (m) i moc (b), co jest wynikiem operacji.

Wykładniki są zwykle stosowane, gdy stosowane są bardzo duże ilości, ponieważ są to nic więcej niż skrót, które reprezentują pomnożenie tej samej liczby. Wykładniki mogą być zarówno pozytywne, jak i negatywne.

Czym są wykładnicy w operacjach matematycznych?

Jak wspomniano powyżej, wykładnicy są formą skróconą, która reprezentuje mnożenie liczb dla siebie, gdzie wykładnik odnosi się tylko do lewej liczby. Na przykład:

2³ = 2*2*2 = 8

W takim przypadku liczba 2 jest podstawą mocy, która zostanie pomnożona 3 razy, jak wskazano przez wykładnik, znajdujący się w prawym górnym rogu podstawy. Istnieją różne sposoby czytania wyrażenia: 2 podwyższone do 3 lub 2 podniesionych do kostki.

Wykładniki wskazują również liczbę razy, które można podzielić, i aby odróżnić tę operację od mnożenia, wykładnik przenosi znak minus (-) przed sobą (jest ujemny), co oznacza, że ​​wykładnik znajduje się w mianowniku dla mianownika frakcja. Na przykład:

2^{- 4} = 1/2*2*2*2 = 1/16

Nie należy tego mylić z przypadkiem, w którym podstawa jest ujemna, ponieważ będzie to zależeć od tego, czy wykładnik jest równy, czy dziwny, aby ustalić, czy moc będzie dodatnia, czy ujemna. W ten sposób musisz:

- Jeśli wykładnik jest równy, moc będzie pozytywna. Na przykład:

(-7)² = -7 _* -7 = 49.

- Jeśli wykładnik jest dziwny, moc będzie ujemna. Na przykład:

(-2)⁵ = (-2)*(-2)*(-2)*(-2)*(-2) = -32.

Istnieje specjalny przypadek, w którym jeśli wykładnik jest równy 0, moc jest równa 1. Istnieje również możliwość, że podstawa wynosi 0; W takim przypadku, w zależności od wykładnika, moc będzie nieokreślona lub nie.

Aby wykonywać operacje matematyczne z wykładnikami, jest konieczne.

Jakie są prawa wykładników?

Pierwsze prawo: moc wykładnika równa 1

Gdy wykładnik wynosi 1, wynik będzie taka sama jak podstawa: a¹ = a.

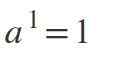
Przykłady

9¹ = 9.

22¹ = 22.

895¹ = 895.

Drugie prawo: moc wykładnika równa 0

Gdy wykładnik wynosi 0, jeśli podstawa różni się od zera, wynik będzie: a⁰ = 1.

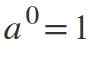
Przykłady

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Trzecie prawo: negatywny wykładnik

Ponieważ wykładnik jest ujemny, wynikiem będzie ułamek, w którym moc będzie mianownikiem. Na przykład, jeśli m jest pozytywny, to^-M = 1/a^M.

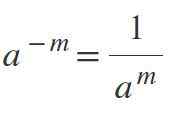
Przykłady

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Czwarte prawo: mnożenie równych uprawnień z tym samym

Aby pomnożyć moce tam, gdzie podstawy są takie same i różnią się od 0, baza jest utrzymywana i dodaje się wykładniki: a^M _* Do^N = a^M+n.    

Przykłady

- 4⁴ _* 4³ = 4⁴⁺³ = 4⁷

- 8¹ _* 8⁴ = 8¹⁺⁴ = 8⁵

- 2² _* 2⁹ = 2²⁺⁹ = 2^jedenaście

Piąte prawo: dział władzy z tą samą bazą

Aby podzielić moce, w których podstawy są takie same i różnią się od 0, podstawa jest utrzymywana, a wykładniki odejmowane są w następujący sposób: a^M / Do^N = a^M-n.    

Przykłady

- 9² / 9¹ = 9 ^{(dwadzieścia jeden)} = 9¹.

- 6^piętnaście / 6¹⁰ = 6 ^(15–10) = 6⁵.

- 49¹² / 49⁶ = 49 ^(12–6) = 49⁶.

Szóste prawo: mnożenie różnych mocy o innej bazie

W tym prawie istnieje przeciwieństwo tego, co wyraża się w czwartym; To znaczy, jeśli masz różne podstawy, ale z tymi samymi wykładnikami, podstawy są mnożone, a wykładnik jest utrzymywany: a^M _* B^M = (a_*B) ^M.

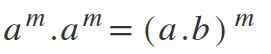
Przykłady

- 10² _* 20² = (10 _* 20)² = 200².

- Cztery pięć^jedenaście _* 9^jedenaście = (45*9)^{11 =} 405^jedenaście.

Innym sposobem reprezentowania tego prawa jest to, że mnożenie jest wysokie dla mocy. Zatem wykładnik będzie należeć do każdego z terminów: (_*B)^M= a^M_* B^M.

Przykłady

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Siódmy prawo: inny podział energetyczny

Jeśli masz różne podstawy, ale przy tych samych wykładnikach zasady są podzielone, a wykładnik utrzymuje się:^M / B^M = (A / B)^M.

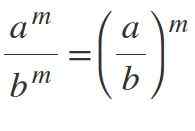
Przykłady

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5.5⁴.

Podobnie, gdy podział jest wysoki do mocy, wykładnik będzie należeć do każdego z terminów: (A / B) ^M = a^M /B^M.

Przykłady

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

Istnieje przypadek, w którym wykładnik jest ujemny. Tak więc, aby być pozytywnym, wartość licznika jest inwestowana w wartość mianownika, w następujący sposób:

- (A / B)^-N = (b / a)^N = b^N / Do^N.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Ósme prawo: moc władzy

Kiedy masz moc podniesioną do innej mocy -to znaczy, dwóch wykładników jednocześnie -baza jest utrzymywana, a wykładnicy mnożą się: (^M)^N= a^M*N.

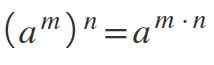
Przykłady

- (8³)² = 8 ^(3*2) = 8⁶.

- (13⁹)³ = 13 ^(9*3) = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Dziewiąte prawo: wykładnik ułamkowy

Jeśli moc ma jako wykładnik frakcję, jest to rozwiązane przez przekształcenie jej w korzeń N-EIMA, gdzie licznik pozostaje jako wykładnik, a mianownik reprezentuje indeks root:

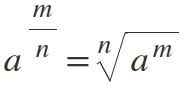
Przykład

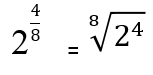
Rozwiązane ćwiczenia

Ćwiczenie 1

Oblicz operacje między uprawnieniami, które mają różne podstawy:

2⁴ _* 4⁴ / 8².

Rozwiązanie

Stosując zasady wykładników, podstawy są mnożone w liczniku, a wykładnik jest utrzymywany, tak:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Teraz, ponieważ istnieją równe zasady, ale przy różnych wykładnikach podstawa jest utrzymywana, a wykładniki odejmowane są:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Ćwiczenie 2

Oblicz operacje między wysokimi uprawnieniami do innej mocy:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

Rozwiązanie

Stosując prawa, musisz:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

= 3⁶ _* 2^-2 _* 2^-10 _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Bibliografia

1. Aponte, g. (1998). Podstawowe podstawy matematyki. Edukacja Pearsona.
2. Corbalán, f. (1997). Matematyka stosowana w życiu codziennym.
3. Jiménez, J. R. (2009). Matematyka 1 września.
4. Max Peters, w. L. (1972). Algebra i trygonometria.
5. Rees, str. K. (1986). Rectte.