Kirchhoff Law

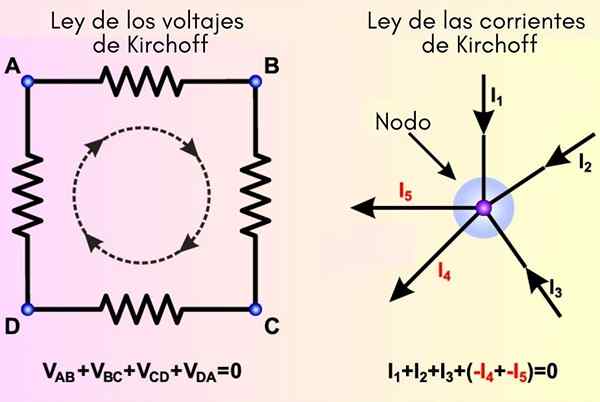
Przepisy Kirchoffa wywodzą się odpowiednio z zasad ochrony energii i obciążenia. Po lewej stronie jest ustanowione prawo siatki, a po prawej stronie prądy

Jakie są prawa Kirchoffa?

Kirchoff Law Polegają one na zastosowaniu zasady zachowania ładunku elektrycznego i zasady ochrony energii na obwody elektryczne, aby rozwiązać te, które mają kilka siatek.

Zasady te, ponieważ nie są prawami w ścisłym sensie, są spowodowane niemieckim fizykiem Gustava Kirchoffa (1824–1887). Jego zastosowanie jest niezbędne, gdy prawo Ohma nie wystarcza do określenia napięć i prądów w obwodzie.

Przed oświadczeniem i zastosowaniem przepisów Kirchoffa wygodnie jest zapamiętać znaczenie niektórych ważnych pojęć dotyczących obwodów elektrycznych:

• Węzeł: Punkt związkowy między dwoma lub więcej przewodowymi przewodami.
• Oddział: Elementy obwodu między dwoma kolejnymi węzłami, przez które krąży ten sam prąd.
• Siatka: trajektoria lub zamknięta pętla złożona z dwóch lub więcej gałęzi, która jest podróżowana w tym samym kierunku, bez przechodzenia przez ten sam punkt.

Pierwsze prawo Kirchoffa

Jest również znany jako prawo prądów lub zasada węzłów i stwierdza, że:

Suma prądów wchodzących do węzła jest równa suma prądów, które z niego wychodzą.

Tak więc w sposób matematyczny pierwsze prawo jest wyrażane jako:

∑ i = 0

Gdzie symbol σ wskazuje sumę.

Poprzednie równanie określa, że ​​ponieważ ładunek elektryczny nie jest tworzony ani niszczony, cały prąd (obciążenie na jednostkę czasu), który wchodzi do węzła, musi być równy temu, który z niego wychodzi.

Może ci służyć: sztuczne satelity

Przykład

Aby wygodnie zastosować prawo prądów, znak jest przypisany do prądów przychodzących. Wybór jest całkowicie arbitralny.

Poniższy obraz pokazuje dwa prądy wprowadzające węzeł, narysowane na czerwono: i₁ i ja₂, i że po wychodzeniu są pokazywane na zielono: prądy i₃, Siema₄ i ja₅.

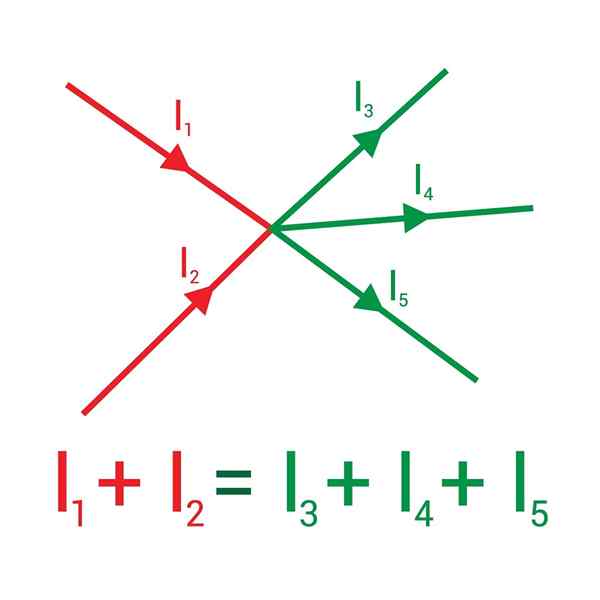Suma prądów wchodzących do węzła jest równa suma prądów, które z niego wychodzą

Przypisanie znaku (+) do prądów przychodzących i (-) do wychodzącego, pierwsza zasada Kirchoffa stwierdza, że:

Siema₁ + Siema₂ - Siema₃ - Siema₄ - Siema₅= 0 ⇒ i₁ + Siema₂ = I₃ + Siema₄ + Siema₅

Drugie prawo Kirchoffa

Inne nazwiska drugiego prawa Kirchoffa to: Prawo napięć, Prawo napięć albo Prawo o siatce. W każdym razie stwierdza, że:

Algebraiczna suma kropli napięcia wzdłuż siatki jest równa 0.

Jest to sposób na zastosowanie ochrony energii w obwodzie, ponieważ napięciem w każdym elemencie jest zmiana energii na jednostkę obciążenia.

Dlatego podczas podróży zamkniętej części (siatki) suma algebraiczna napięcia wzrasta i upadki wynosi 0 i może być napisane:

∑ v = 0

Przykład

Na poniższej liczbie masz siatkę Abcda, przez który prąd krąży w kierunku igieł zegara, a trasa może zacząć się w dowolnym punkcie obwodu.

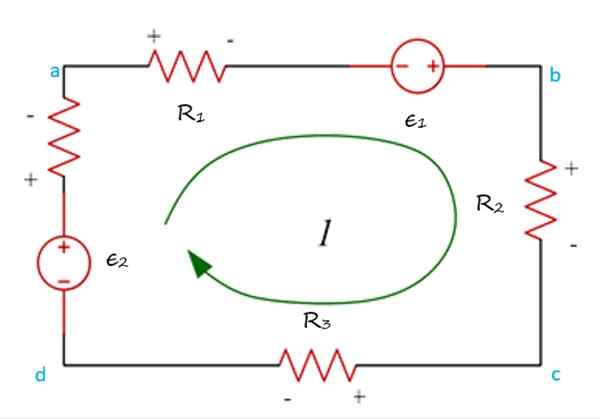Przykład siatki koncertował w harmonogramie, w którym wykazano, że wzrost i potencjalne upadki stosują prawo napięć Kirchoffa. Źródło: f. Zapata.

Jest to również konieczne. Zwykle jest przypisanie jako dodatnie wzrost napięcia, to znaczy, gdy prąd krąży z ( - -) do (+). Następnie spadek napięcia, który występuje, gdy prąd przechodzi z (+) do ( -), jest ujemny.

Może ci służyć: tlenek krzemu (SiO2): struktura, właściwości, użycie, uzyskiwanie

Uruchamianie trasy siatki w punkcie „A” jest oporem r₁. W nim obciążenia doświadczają potencjalnej kropli, symbolizowanej przez znaki (+) po lewej stronie i ( -) powyżej oporu.

Dlatego napięcie lub napięcie w r₁ Ma znak ujemny.

Następnie osiągasz bezpośrednie źródło napięcia, zwane ε₁, którego biegunowość jest mniejsza (-) Więcej (+). Tam ładunki elektryczne przechodzą potencjalny wzrost, a to źródło jest uważane za pozytywne.

Zgodnie z tą procedurą pozostałego oporu i drugiego źródła w rezultacie uzyskuje się następujące równanie:

−v₁ + ε₁ - V₂ - V₃ + ε₂ = 0

Gdzie v₁, V₂ i v₃ są napięciami w opornościach r₁, R₂ i r₃. Te napięcia można znaleźć na podstawie prawa Ohma: v = i · r.

Ćwiczenie rozwiązane

Znajdź wartość prądów i₁, Siema₂ i ja₃ pokazane na rysunku.

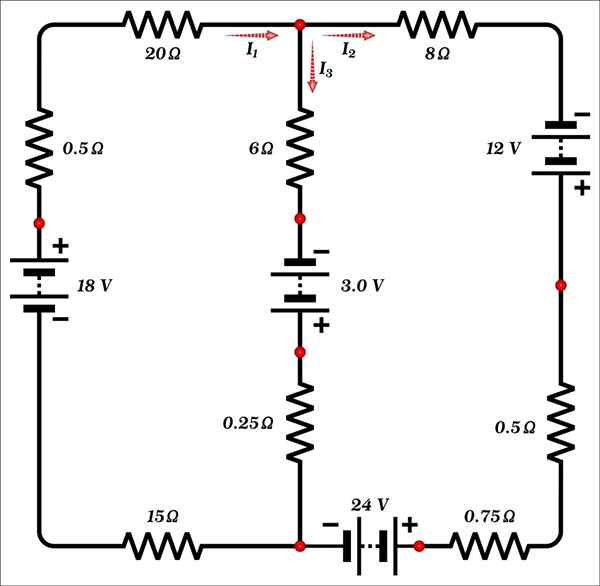
Rozwiązanie

Ten obwód składa się tylko z dwóch siatek i ma 3 niewiadome: prądy i₁, Siema₂ i ja₃, więc co najmniej 3 równania są wymagane do znalezienia rozwiązania.

W węźle (punkt zaznaczony na czerwono), który znajduje się u góry obwodu na gałęzi środkowej, obserwuje się, że prąd i₁ przychodzą, a prądy i₂ i ja₃ Są towarzyszące.

Dlatego prawo prądów Kirchoffa prowadzi do pierwszego równania:

1) i₁ - I₂ - I₃ = 0

Dolny węzeł podaje te same informacje, dlatego następnym krokiem jest podróżowanie po siatkach.

Pierwsza siatka

Aby ustanowić następujące równanie, siatka po lewej stronie jest podróżowana w harmonogramie, zaczynając od lewego górnego rogu. To jest sens krążących prądów i prądów₁ i ja₃.

Może ci służyć: komparator optyczny: do czego to jest i części

Zauważ, że:

• Siema₁ przechodzi przez rezystancje 20 Ω, 15 Ω i 0.5 Ω i bateria 18 V, gdzie ma potencjalny wzrost.
• Ze swojej części, ja₃ Przecina rezystancje gałęzi środkowej 6 Ω i 0.15 Ω i na 3 baterii.0 V to potencjalny wzrost.

Podobnie, prawo OHM V = I ∙ R jest używane do ustalenia napięcia w każdym oporze, zgodnie z tym:

−20 ∙ i₁ - 6 ∙ i₃ + 3.0 - 0.25 ∙ i₃ −15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

Zamawianie warunków:

(−20 −15–0.5) ∙ i₁ - (6 + 0.25) ∙ i₃  = - 3.0 - 18.0

−35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ i₁ + 6.25 ∙ i₃ = 21.0

Druga siatka

Trzecie równanie jest uzyskiwane przez zwiedzanie siatki po prawej stronie, zaczynając od węzła górnego obwodu. Obserwuje się, że:

• Siema₂ Przejdź przez rezystancje 8 Ω, 0.5 Ω i 0.75 Ω, plus baterie 12 V i 24 V. Według polaryzacji baterii na trasie wzrost potencjału w 12 V i spadek 24 V.
• Ważny: Zwiedzanie drugiej siatki (w harmonogramie) jest przeciwne I₃, Dlatego napięcia w rezystancji 6 Ω i 0.25 Ω to potencjalne podwyżki i noszą znak dodatni. Według polaryzacji baterii rośnie wzrost 12 V i spadek w 24 V i 3 V.

Z tym wszystkim docierasz:

−8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ i₃ = 0

3) −25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Obliczanie bieżących

Równania 1), 2) i 3) tworzą układ 3 równania liniowe z 3 niewiadomymi, których rozwiązaniem jest:

Siema₁ = 0.381 a; Siema₂ = -0.814 A; Siema₃ = 1.195 a

Znak ujemny w bieżącym i₂ oznacza, że ​​płynie w przeciwnym kierunku od schematu.