Prawo Ficka

Jakie jest prawo Ficka?

Prawo Ficka Jest to równanie matematyczne, które wiąże przepływ masy rozpowszechniony w pożywce o stężeniach lub gradiencie ciśnienia. Został sformułowany w 1855 r. Przez niemieckiego fizjologa i doktora Adolfa Ficka, który zainspirował prawa Fouriera (przewodnictwo termiczne) i Ohm (przewodnictwo elektryczne), modelował proces dyfuzji tlenu do pęcherzyków płucnych płuc.

Prawo Ficka przedstawia specyfikę, że ma ona nie tylko zjawiska chemiczne lub biochemiczne dyfuzji, ale także do jakichkolwiek rodzaju natury. Dlatego służy modelowaniu rozpowszechniania atomów między ciałami stałymi, ponieważ jest bardzo przydatny w fizyce materiałów i inżynierii.

Reprezentacja procesu dyfuzji przez półprzepuszczalną błonę. Źródło: Gabriel Bolívar.

Jednak centralna baza jest taka sama dla prawie wszystkich zjawisk dyfuzji, co jest zilustrowane powyżej. Cząsteczki fioletowe, są atomami lub cząsteczkami, rozprzestrzeniają się przez półprzepuszczalną grubą błonę L i obszar poprzeczny do. Po lewej stronie mamy większe stężenie C₁ cząstek, które po prawej, c₂.

Prawo Ficka określa następujące czynności: przepływ masowy, który jest rozpowszechniany przez powierzchnię, jest proporcjonalny do gradientu stężenia (c₂-C₁/L) i stała D zwana współczynnikiem dyfuzji lub dyfuzyjności.

To prawo ma dwie formy: jedna oparta na przestrzeni (x), a druga w zależności od przestrzeni i czasu (x, t). Pierwszy ma zastosowanie do systemów w warunkach stacjonarnych, a drugi dla prawdziwych, niezwiązanych systemów.

Pierwsze prawo Ficka

Komponenty i równanie

Gruba l półprzepuszczalnej membrany reprezentuje odległość (x), którą cząstki muszą podróżować, aby dotrzeć do drugiej strony. Jak widać na obrazie, fioletowe cząstki im bardziej odchodzą od lewego przedziału, gdzie C₁ Jest świetny, jego stężenie zmniejsza się do wartości C₂. Oznacza to, że stężenie zmienia się wzdłuż grubości błony, zależnie od x.

Ta zmienność stężenia w zależności od odległości jest tak zwana gradient stężenia: (C₂-C₁)/L o (c₂-C₁)/X. Zauważ, że jego wartość jest ujemna (-1), ponieważ c₂ > C₁.

Z drugiej strony mamy również prędkość, z jaką cząstki są rozprzestrzeniane przez membranę lub przedmiotową przestrzeń. Ta prędkość zależy od wielkości i masy cząstek, a także od charakteru środowiska i temperatury. Współczynnik dyfuzji D reprezentuje tę prędkość i może być stały lub nie podczas dyfuzji.

Może Ci służyć: filtr laboratoryjny): Charakterystyka, funkcje, typy

I wreszcie, mamy przepływ masowy „J”, który przecina powierzchnię poprzeczną błony lub kanał, w którym rozprzestrzeniły się cząsteczki. Grupując niniejsze warunki, rodzi się równanie pierwszego prawa Ficka:

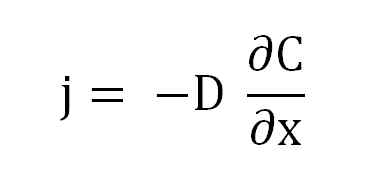Równanie pierwszego prawa Ficka. Źródło: Gabriel Bolívar.

Gdzie j jest proporcjonalny do d i a (∂c/∂x), gradient stężenia.

Interpretacja i jednostki

Symbol ujemny w równaniu służy do neutralizowania negatywnego znaku gradientu stężeń. W przeciwnym razie J miałby wartość ujemną, która jest niezamieszkana. Podobnie wartość D jest dodatnia, więc przez pomnożenie przez poprzedni znak ujemny, daje wartość ujemną.

Pierwsze prawo Ficka wskazuje: im większy gradient stężenia (∂c/∂x), tym większy przepływ masy j. To znaczy różnica między C₂ i C₁ Staje się większy, a zatem więcej cząstek rozprzestrzeni się przez membranę.

Z drugiej strony J zależy również od D, który z kolei zależy od parametrów, takich jak temperatura, lepkość, masa cząsteczkowa i powierzchnia poprzeczna do:

D ∝ (a/l) (s/√m_W)

Gdzie S jest rozpuszczalnością cząstki, która jest rozprzestrzeniona w środowisku, oraz m_W Jego masa cząsteczkowa.

Jeśli chodzi o jednostki komponentów lub warunków równania, które mamy:

-C (kg · m^-3 lub mol · m^-3)

-D (m^-2· S^-1)

-J (kg · m^-2· S^-1 lub mol · m^-2· S^-1)

Średnie przemieszczenie netto kwadratowe

Podczas rozprzestrzeniania cząstki zderzają się ze sobą, a po krótkich przedziałach czasowych przebywają ogromne odległości δx. Jednak w zależności od znaczenia tych przesunięć δx może mieć wartości ujemne lub dodatnie (zgodnie z punktem pochodzenia). Dlatego średnia wartości δx dla wszystkich cząsteczek ma tendencję do 0.

Z drugiej strony wartości δx są bardzo małe w porównaniu z odległościami, które uruchamiają cząstki. Kiedy zderzają się, tracą mobilność w kierunku, w konsekwencji o ograniczonym przesiedleniu netto; Na przykład 2 cm postępuje w jednym kierunku po podróży setki metrów w kolizjach i zbiórkach.

Einstein w 1905 r. Znalazł matematyczne wyrażenie dla średniego przewijania przemieszczenia (dlatego różni się od 0):

<(Δx)²> = 2dt

Definiowanie

(Δx)_RMS ≡ <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_RMS Jest to średnie przesunięcie kwadratowe netto omawianych cząstek. (Δx)_RMS Według czasu mówi nam, ile cząstek porusza się średnio (w kierunku dodatnim lub ujemnym). Niektóre cząstki będą poruszać się dalej lub najbliższe odległości niż (δx)_RMS, powodując rozkład Gaussa.

Może ci służyć: tlenek wapnia (CAO)

Fick drugie prawo

Równanie

Pierwsze prawo Ficka opisuje dyfuzję w warunkach stacjonarnych, to znaczy przepływ masowy J nie zmienia się w czasie. Jednak w prawdziwych systemach mamy warunki nietracjonalne, w których przepływ masy nie tylko zmienia się w przestrzeni, ale także z czasem. Dlatego jest zainteresowany określeniem (∂c/∂t).

Poniżej mamy dwa równania, które reprezentują drugie prawo Ficka:

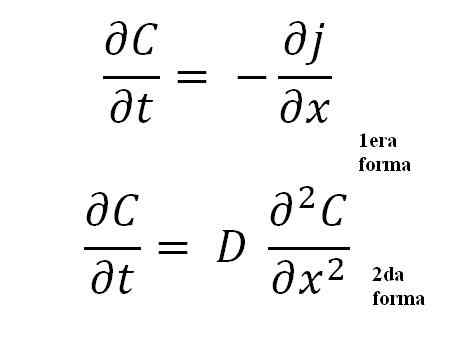Równania drugiego prawa Ficka. Źródło: Gabriel Bolívar.

Druga forma jest najważniejsza ze wszystkich, ponieważ reprezentuje ogólne równanie matematyczne dla każdego procesu rozpowszechniania; Albo termiczne, elektryczne, atomowe itp.

Odliczenie

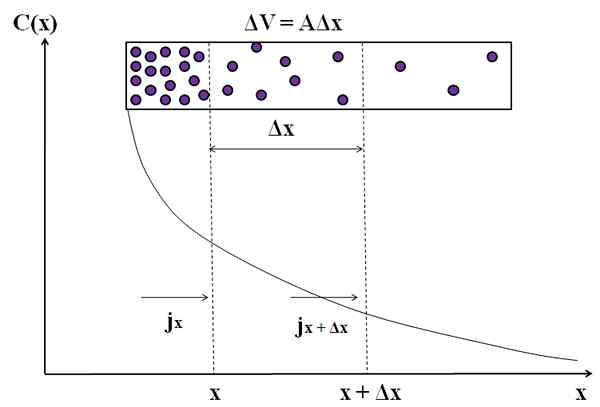Graficzna reprezentacja tego, jak przepływ masy nie jest stały w rozpowszechnianiu tych cząsteczek. Źródło: Gabriel Bolívar.

Rozważ ponownie fioletowe cząstki w prostokątnej komorze. Wśród odległości x i x+δx mamy przepływ j_X (przychodzące) i J_x+δx (towarzyski). Objętość aparatu między tymi odległościami jest zdefiniowana przez:

ΔV = aΔx

Zauważ, że wykres c (x) vs x nie powstaje linii prostej, więc mamy różne wartości j (j_X ≠ j_x+δx). Musimy określić ΔC/δt.

Masa m_X Będzie to równe:

M_X = J_X AΔt

Analiza wymiarowa pomaga zrozumieć, dlaczego:

kg = (kg · m^-2· S^-1) (M²) (S)

W ten sam sposób obliczamy m_x+δx:

M_{x+ δx} = J_x+δx AΔt

Będąc masą, która gromadzi się w tym regionie równa Δm:

ΔM = m_X - M_{x+ δx}

= (j_X - J_{x+ δx}) AΔt

= -(j_{x+ δx} - J_X) AΔt

= -JęjaΔt

I wiedząc, że δC = ΔM/δv

ΔC = -JaΔt/ δv

= -JAδT /AΔx

= -JΔt/δx

Oczyszczamy ΔC/δt

ΔC/δT = -ΔJ/δx

To wyrażenie wskazuje, że zmiana stężenia w czasie jest równa zmiany przepływu J w odniesieniu do jego przemieszczenia. Stosując granice dla δT i δX do 0, otrzymujemy to samo wyrażenie co częściowa pochodna:

∂c/∂t = -(∂j/∂x) (1. forma)

Wreszcie, drugi formularz jest uzyskiwany przez zastąpienie pierwszego prawa Ficka:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (2. forma)

Rozwiązane ćwiczenia

W poniższych ćwiczeniach będą rozważane bardzo proste systemy, których niewiadomy można rozwiązać za pomocą pierwszego prawa Ficka.

Ćwiczenie 1

Oświadczenie

W rurze o długości 15 metrów i 21 centymetrów, a także nasycona azotem, prąd tlenu rozprzestrzenia się z jednego końca na drugie w temperaturze 0 ° C. Wiedząc, że nacisk po lewej stronie (str₁) to 20 kg/m³, I że nacisk po prawej stronie (str₂) Wynosi 10 kg, określ:

Może ci służyć: hydronio jon

a) Rozprzestrzeniający się przepływ masy

b) Ile kilogramów lub₂ Rozprzestrzenią się w rurze za 17 minut?

c) gradient stężenia lub ciśnienia

d) ciśnienie O₂ w odległości 7 metrów od wejścia do rurociągu

e) Ile będzie 80 kg O₂ Rozprzestrzeniając się przez tę fajkę?

Rozważ to d_O2-N2 jest równe 1.8 · 10^-5 M²· S^-1.

Rezolucja

Z pierwszego prawa Ficka musimy rozwiązać podsekcję A):

J = -d (p₂-P₁)/L

= -(1.8 · 10^-5 M²· S^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

Do b) potrzebujemy obszaru rur:

A = π (0.21 m)²

= 0.14 m²

I rozmnażamy J przez a i czas t, aby określić masę lub₂ Zwolniony:

M_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Teraz dla podsekcji C) mamy, że gradient jest równy:

Gradient = (p₂-P₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Ale przyjmujemy wartość dodatnią, co ma sens fizyczny:

2/3 (kg/m³) · M^-1

Ta wartość będzie nam służyć do rozwiązania podsekcji d) Jeśli gradient zostanie dobrze interpretowany: każdy miernik ciśnienia₂ Spadnie 2/3 kg/m³. Rozprowadzając 7 metrów: będziemy mieli:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 lub 4.7 kg/m³

Oznacza to, że ciśnienie w tej odległości będzie:

(20-4.7) (kg/m³) = 15.3 kg/m³

I wreszcie podsekcja e) jest podobna do B), tylko że teraz usuwamy czas, a nie masę:

M_O2 = Jat

t = m_O2/JA

= (80 kg)/(1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²)

= 47619.04 s lub 0.55 dni

Ćwiczenie 2

Oświadczenie

Określić (δx)_RMS Dla sacharozy w wodzie przy t = 1 min, 1 h i 1 dzień. Współczynnik rozprzestrzeniania sacharozy w wodzie wynosi 0.52 · 10^-5cm²· S^-1.

Rezolucja

Stosujemy równanie:

(Δx)_RMS ≡ <(Δx)²>^1/2 = (2dt)^1/2

Oceniamy (δx)_RMS Z czasami wyrażonymi w kilka sekund. Dla t = 1 min lub 60 s:

(Δx)_RMS = ((2 (0.52 · 10^-5cm²· S^-1) (60s))^1/2

= 0.025 cm

Dla t = 1 h lub 3600 s:

(Δx)_RMS = ((2 (0.52 · 10^-5cm²· S^-1) (3600S))^1/2

= 0.19 cm

I wreszcie dla t = 1 dzień lub 86400 s:

(Δx)_RMS = ((2 (0.52 · 10^-5cm²· S^-1) (86400S))^1/2

= 0.95 cm

Zauważ, że w miarę upływu czasu cząsteczki sacharozy nie były nawet w stanie poruszać 1 cm w żadnych kierunkach.

Bibliografia

1. Walter J. Moore. (1963). Chemia fizyczna. W kinetyce chemicznej. Czwarta edycja, Longmans.
2. Iran. Levine. (2009). Zasady fizykochemii. Szósta edycja. MC Graw Hill.
3. Wprowadzenie do materiałów materiałowych i inżynierii. (11 marca 2018 r.). Drugie prawo Ficka. Prof. Rajesh Prasad. [WIDEO]. Odzyskane z: YouTube.com
4. Wikipedia. (2020). Prawo rozpowszechniania Ficka. Źródło: w:.Wikipedia.org
5. Laura Dickson. (10 września 2020). DYFUZJA. Chemia librettexts. Odzyskane z: chem.Librettexts.org
6. Larissa Zhou i in. (1 września 2015 r.). Zrozumienie teorii dyfuzji i prawa Ficka poprzez jedzenie i gotowanie. Amerykańskie społeczeństwo fizjologiczne. doi.Org/10.1152/Advan.00133.2014