Prawo piwa-lambert

Jakie jest prawo Beer-Lambe?

Prawo piwa-lambert (Beer-Bouguer) to taki, który wiąże wchłanianie promieniowania elektromagnetycznego jednego lub większej liczby gatunków chemicznych, z jego stężeniem i odległością, która prowadzi światło w interakcjach cząstek-fotonu. To prawo łączy dwa prawa w jednym.

Prawo Bouguera (choć uznanie upadło bardziej na temat Heinricha Lamberta), stwierdza, że ​​próbka pochłonie większe promieniowanie, gdy wymiary środowiska chłonnego lub materialnego są większe; w szczególności jego grubość, która staje się odległością L który biegnie przez światło podczas wchodzenia i wychodzenia.

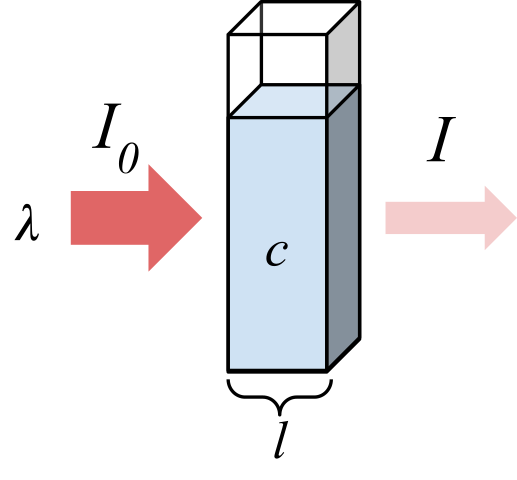Promieniowanie pochłonięte przez próbkę. Źródło: Marmot2019 [CC BY-SA 4.0 (https: // creativeCommons.Org/licencje/nabrzeże/4.0)], z Wikimedia Commons

Najwyższy obraz pokazuje wchłanianie promieniowania monochromatycznego; to znaczy złożona z jednej długości fali, λ. Pożywka chłonna znajduje się wewnątrz komórki optycznej, której grubość jest L, i zawiera gatunki chemiczne ze stężeniem C.

Wiązka światła ma początkową i końcową intensywność, oznaczoną z symbolami i₀ i ja odpowiednio. Zauważ, że po interakcji z medium chłonnym i jest mniej niż ja₀, co pokazuje, że było wchłanianie promieniowania. Im są starsi C I L, mniejsze będzie ja w odniesieniu do i₀; to znaczy będzie więcej wchłaniania i mniej transmitancja.

Wyjaśnienie prawa Beer-Lambe

Najwyższy obraz doskonale obejmuje to prawo. Absorpcja promieniowania w próbce wzrasta lub maleje wykładniczo w zależności od C albo L. Aby prawo było całkowicie i łatwo zrozumieć, konieczne jest obramowanie jego aspektów matematycznych.

Jak już wspomniano, ja₀ I jestem intensywnością monochromatycznej wiązki światła przed i po świetle,. Niektóre teksty wolą używać symboli P₀ i p, które nawiązują do energii promieniowania, a nie do jej intensywności. Tutaj wyjaśnienie będzie nadal wykorzystywać intensywności.

Może ci służyć: acetofenon

Aby zlinearyzować równanie tego prawa, należy zastosować logarytm, zwykle podstawa 10:

Log (i₀/I) = εlC

Termin (ja₀/I) wskazuje, jak bardzo zmniejsza się intensywność promieniowania iloczynu absorpcji. Prawo Lamberta uważa tylko L (εL), podczas gdy piwo ignoruje L, ale umieszcza C Zamiast tego (εC). Wyższe równanie jest zjednoczeniem obu praw, a zatem jest ogólnym matematycznym wyrażeniem prawa piwa-lambe.

Absorbancja i transmitancja

Absorbancja jest zdefiniowana przez termin dziennik (i₀/SIEMA). Zatem równanie wyraża się w następujący sposób:

A = εlC

Gdzie ε jest współczynnikiem ekstynkcji lub absorganizacji molowej, co jest stałą przy określonej długości fali.

Należy zauważyć, że jeśli grubość pochłaniania pozostaje stała, podobnie jak ε, absorbancja zależy wyłącznie od stężenia C, gatunków chłonnych. Ponadto jest to równanie liniowe, y = mx, gdzie I jest i X Jest C.

Wraz ze wzrostem absorbancji zmniejsza się przekazanie; To jest, ile promieniowania udaje się przesyłać po wchłanianiu. Dlatego są odwrotne. Tak₀/I wskazuje stopień wchłaniania, i/i₀ Jest równy transmitancji. Wiedząc o tym:

I/ja₀ = T

(SIEMA₀/I) = 1/t

Log (i₀/I) = log (1/t)

Ale log (ja₀/I) Jest również równe absorbancji. Zatem związek między t jest:

A = log (1/t)

I zastosowanie właściwości logarytmów i wiedza, że ​​log1 jest równy 0:

A = -logt

Zwykle transmisje są wyrażane w wartościach procentowych:

%T = i/i₀∙ 100

Wykresy

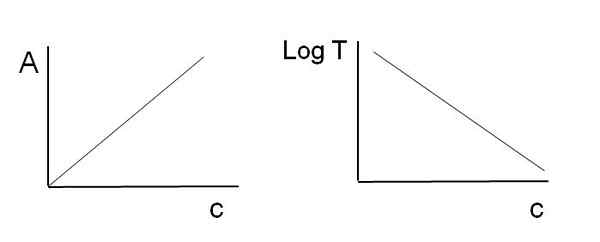
Jak wspomniano powyżej, równania odpowiadają funkcji liniowej; Dlatego oczekuje się, że podczas ich wykresu da linię.

Może ci służyć: jaka jest kinetyka chemiczna? Grafika używana do prawa piwa-lambert. Źródło: Gabriel Bolívar

Zwróć uwagę, że po lewej stronie powyższego obrazu uzyskano linię podczas wykresu przeciwko C, a po prawej linia odpowiadająca wykresowi logt C. Jeden ma dodatnie nachylenie, a drugi negatywny; Im większa absorbancja, tym niższa transmitancja.

Dzięki tej liniowości stężenie chłonnych gatunków chemicznych (chromoforów) można określić, czy wiadomo, ile promieniowania pochłaniają (a), czy też jest przenoszone przez promieniowanie (logt). Kiedy ta liniowość nie jest obserwowana, mówi się, że jest on odchylenie.

Zastosowania prawa piwa-lambe

Ogólnie rzecz biorąc, niektóre z najważniejszych zastosowań tego prawa są wspomniane poniżej:

-Jeśli gatunek chemiczny ma kolor, jest to przykładowy kandydat do analizy technikami kolorymetrycznymi. Opierają się one na prawie piwa i pozwalają na określenie stężenia analitów na podstawie absorbancji uzyskanych za pomocą spektrofotometru.

-Pozwala na budowę krzywych kalibracji, z którymi biorąc pod uwagę efekt macierzy próbki, określone jest stężenie gatunku.

-Jest szeroko stosowany do analizy białek, ponieważ kilka aminokwasów ma ważne absorpcje w regionie ultrafioletowym widma elektromagnetycznego.

-Reakcje chemiczne lub zjawiska molekularne, które sugerują zmianę kolorowania, można analizować za pomocą wartości absorbancji, przy jednej lub więcej długościach fal.

-Tworząc analizę wielowymiarową, można analizować złożone mieszaniny chromoforów. W ten sposób można określić stężenie wszystkich analitów, a także klasyfikować mieszaniny i odróżnić je od siebie; Na przykład, wyklucz, czy dwa identyczne minerały pochodzą z tego samego konkretnego kontynentu lub kraju.

Może ci służyć: silny kwas

Rozwiązane ćwiczenia

Ćwiczenie 1

Jaka jest absorbancja roztworu, która przedstawia 30% transmitancję do długości fali 640 nm?

Aby to rozwiązać, po prostu przejdź do definicji absorbancji i transmitancji.

%T = 30

T = (30/100) = 0,3

I wiedząc, że a = -logt, obliczenia jest bezpośrednie:

A = -log 0,3 = 0,5228

Zauważ, że brakuje ci jednostek.

Ćwiczenie 2

Jeśli rozwiązanie poprzedniego roku składa się z gatunku W, którego stężenie wynosi 2,30 ∙ 10^-4 M, i zakładając, że komórka ma grubość 2 cm: jakie powinno być jej stężenie, aby uzyskać 8% transmitancję?

Można go rozwiązać bezpośrednio z tym równaniem:

-Logt = εlC

Ale wartość ε jest nieznana. Dlatego należy go obliczyć na podstawie poprzednich danych i zakłada się, że pozostaje on stały w szerokim zakresie stężeń:

ε = -logt/lC

= (-Log 0,3)/ (2 cm x 2,3 ∙ 10^-4 M)

= 1136,52 m^-1∙ cm^-1

A teraz możesz obliczyć za pomocą %t = 8:

C = -Logt/εl

= (-Log 0,08)/ (1136,52 m^-1∙ cm^-1  x 2 cm)

= 4,82 ∙ 10^-4 M

Następnie wystarczy, aby gatunki W podwoili swoje stężenie (4,82/2,3), aby zmniejszyć procent transmitancji o 30% do 8%.

Bibliografia

1. Prawo piwa-lambert. Chemia librettexts. Odzyskane z: chem.Librettexts.org
2. Prawo piwa-lambert. Odzyskane z: chemguide.współ.Wielka Brytania