AMPère Formuła i równania prawo, demonstracja, ćwiczenia

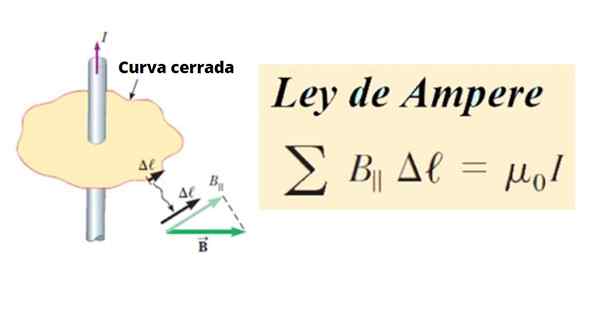
Prawo ampère stwierdza, że ​​krążenie wektora indukcyjnego magnetycznego B Jest proporcjonalny do intensywności i prądu, który płynie przez to samo.

Z kolei krążenie B Jest to suma wszystkich produktów między składnikiem stycznym B_║ i długość małego segmentu Δℓ zamkniętej krzywej c, Wokół obwodu. W kategoriach matematycznych jest tak napisane:

∑ b_║ .Δℓ ∝ Siema

Rysunek 1. Definicja prawa ampere. Źródło: Serway, r. Fizyka uczelni.

Jako dowolna linia lub krzywa, można ją podzielić na małe segmenty Δℓ, I to z kolei mogą być nieskończenie małe, a następnie nazywają się Dℓ.

W tym przypadku suma staje się integralną linią produktu skalarnego między wektorami B i dS. Ten produkt zawiera składnik styczny B, który jest B cosθ, gdzie θ jest kątem między wektorami:

Mały okrąg, który przekracza całkę, oznacza, że ​​integracja jest przeprowadzana na zamkniętej trajektorii C, która w tym przypadku obejmuje prąd przepływający przez przekrój kierowcy.

Stała proporcjonalności niezbędna do ustalenia równości wynosi μ_albo, Przepuszczalność próżni. W ten sposób pozostaje prawo Ampère:

Prawo Ampère mówi nam, że integralna linia ∫_C B ∙ dS Jest wart dokładnie μ_alboJa, ale nie oferuje nam szczegółów na temat tego, jak zorientowane jest pole magnetyczne B Dotyczące krzywej C w każdym punkcie lub w zakresie obliczenia całki. Mówi nam tylko, że wynikiem tego samego jest zawsze μ_alboSiema.

[TOC]

Demonstracja prawa Ampère

Prawo Ampère jest weryfikowane eksperymentalnie sprawdzanie pola magnetycznego wytwarzanego przez bardzo długi przewodnik prostoliniowy. Przed rozwiązaniem problemu należy podkreślić dwa przypadki szczególnego zainteresowania poprzednim równaniem:

Może ci służyć: ciała świetliste: cechy i sposób, w jaki generują własne światło

-Pierwszy to kiedy B i dS Są równoległe, co oznacza to B jest styczne do c. Wtedy kąt między obiema wektorami wynosi 0º, a produkt skalarny jest po prostu produktem wielkości B.ds.

-Drugi występuje, jeśli B i dS Są prostopadłe, w takim przypadku produkt skalarny wynosi 0, ponieważ kąt między wektorami wynosi 90º, którego cosinus wynosi 0.

Kolejnym ważnym szczegółem jest wybór krzywej C, na której oceniana jest krążenie pola. Prawo Ampère nie określa, co może być, ale musi zawinąć bieżącą dystrybucję. Nie mówi też, jak podróżować po krzywej i istnieją na to dwie możliwości.

Rozwiązaniem jest przypisanie znaków zgodnie z prawą zasadą kciuka. Cztery palce są zakrzywione w kierunku, w którym chcesz się zintegrować, zwykle będzie to takie same w terenie B krąży. Jeśli bieżące punkty w kierunku prawego kciuka, znak jest przypisany, a jeśli nie, podpisz -.

Ma to zastosowanie, gdy istnieje rozkład z kilkoma prądami, niektóre mogą być pozytywne i inne ujemne. Suma algebraiczna jest tym, co zamierzamy umieścić w prawie Ampère, które jest zwykle mianowane jako Niewinny prąd (Dla krzywej C).

Pole magnetyczne drutu prostoliniowego i nieskończonego

Rysunek 2 pokazuje drut, który przenosi prąd i poza samolotem. Prawidłowa zasada kciuka zapewnia to B Krąży w przeciwnym kierunku, opisując obwody jako pokazują czerwone strzałki.

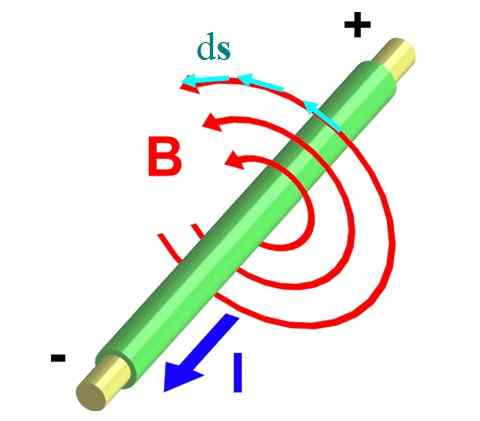Rysunek 2.- Pole magnetyczne nieskończonego drutu. Źródło: Wikimedia Commons.

Weźmy jednego z nich, którego promień jest r. Dzielimy go na małe segmenty różnicowe dS, reprezentowane za pomocą niebieskich wektorów. Oba wektory, B i dS, Są one równoległe w każdym punkcie obwodu, a w ten sposób całka ∫_C B ∙ dS Przekształca się w:

Może ci służyć: prąd stały

∫_C BDS

Jest tak, ponieważ, jak powiedzieliśmy wcześniej, produkt skalarny B ∙ dS  Jest to produkt wielkości wektorów przez cosinus 0º. Wynik całki jest znany dzięki prawu Ampère, dlatego piszemy:

∫_C BDS = μ_alboSiema

Ponieważ wielkość pola jest stała na całej trajektorii, pozostawia całkę:

B ∫_C Ds = μ_alboSiema

Integralna ∫_C DS reprezentuje sumę wszystkich nieskończonych segmentów, które tworzą obwód radiowy R, Równoważny jej długości, iloczyn jego promienia przez 2π:

B.2πr = μ_alboSiema

I stamtąd stwierdzamy, że wielkość B jest:

B = μ_alboI / 2πr

Konieczne jest podkreślenie, że nawet jeśli wybrana trajektoria (lub obwód amperski) Nie okrągłe, wynikiem całki nadal wynosi μ_alboJa jednak ∫_C B ∙ dS To nie byłoby B.2πr.

Dlatego przydatność prawa Ampère do ustalenia pola magnetycznego polega na wyborze rozkładów o wysokiej symetrii, tak że całka jest łatwa do oceny. Trajektorie okrągłe i prostoliniowe spełniają ten wymóg.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Rozważ krzywe A, B, C i D pokazane na rycinie 3. Owijają trzy prądy, dwa, które opuszczają płaszczyznę, symbolizowane jednym punktem ( . ), których intensywności wynosi 1 A i 5 A, a prąd wchodzący do płaszczyzny, który jest oznaczony krzyżem i którego wielkość wynosi 2 A.

Znajdź prąd zamknięty przez każdą krzywą.

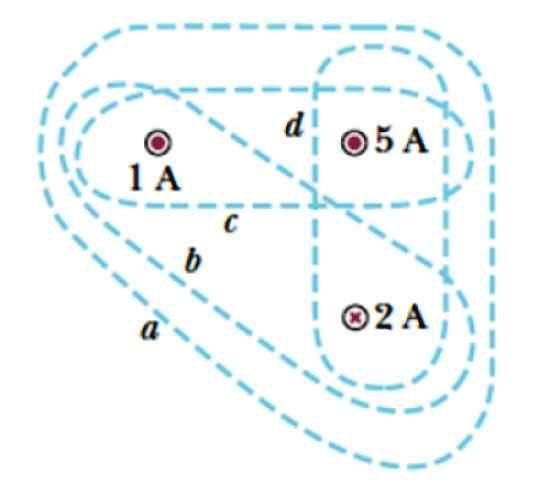Rysunek 3. Kilka krzywych do zastosowania prawa Ampère. Źródło: Serway, r. Fizyka uczelni.

Rozwiązanie

Prądy, które pozostawiają papier, przypisane są znak +. Według tego:

Może ci służyć: powierzchowne fale: cechy, typy i przykłady

Krzywa a

Otacza trzy prądy, dlatego załączony prąd wynosi + 1 a + 5 a - 2 a = 4 a.

Krzywa b

Tylko prądy 1 a y - 2 a są wewnątrz tej krzywej, dlatego zamknięty prąd pochodzi od - 2 a.

Krzywa c

Zawiera prądy wychodzące 1 i 5a, dlatego załączony prąd wynosi 6 A.

Krzywa d

Prądy w środku to +5 a i - 2 a, a następnie otacza prąd netto od 3 do.

- Ćwiczenie 2

Oblicz wielkość pola magnetycznego wytwarzanego przez bardzo długi drut prostoliniowy.

Rozwiązanie

Zgodnie z prawem Ampère, pole drutu jest podawane przez:

B = μ_alboI / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Bibliografia

1. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 6. Elektromagnetyzm. Pod redakcją Douglas Figueroa (USB).
2. Knight, r.  2017. Fizyka dla naukowców i inżynierii: podejście strategiczne.  osoba.
3. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Głośność 2.
4. Serway, r. 2009. Fizyka uczelni. Cengage Learning.
5. Tipler, str. (2006) Physics for Science and Technology. Ed. Głośność 2. Redakcja Reverted.