Multiplikatywne odwrotne wyjaśnienie, przykłady, ćwiczenia rozwiązane
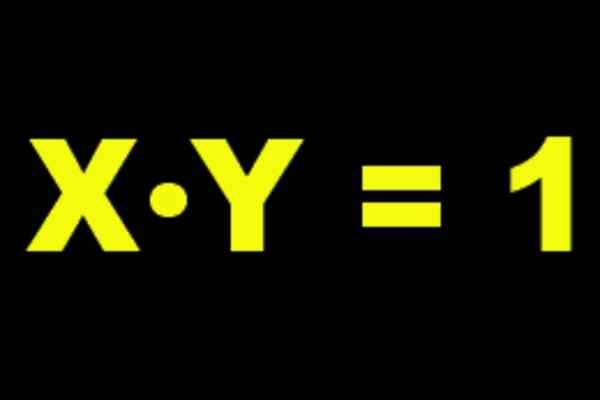
- 1425
- 127
- Bertrand Zawadzki
Jest to rozumiane przez Odwrotna mnożnik jednej liczby, inna liczba, która pomnożona przez pierwsze wyniki w neutralnym elemencie produktu, to znaczy jednostka. Jeśli masz prawdziwą liczbę Do wtedy jego multiplikatywna odwrotność jest oznaczona przez Do-1, I spełnia się, że:
a-1 = a-1 A = 1
Zwykle liczba Do Należy do zestawu liczb rzeczywistych.
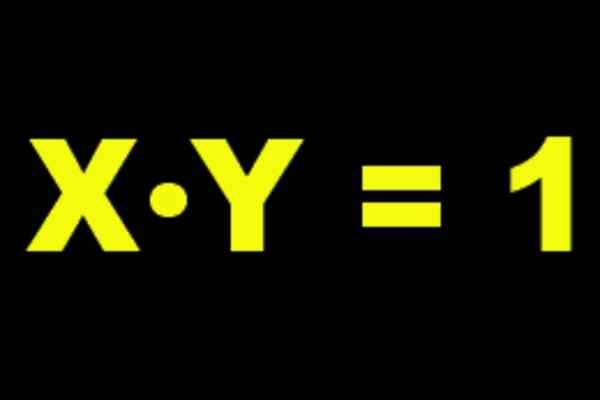 Rysunek 1. I jest odwrotna multiplikatywna x i x jest multiplikatywną odwrotnością y.
Rysunek 1. I jest odwrotna multiplikatywna x i x jest multiplikatywną odwrotnością y. Jeśli na przykład weźmiemy A = 2, Wtedy twoja multiplikatywna odwrotność jest 2-1 = ½ Ponieważ następujące są weryfikowane:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Do Odwrotna mnożnik liczby nazywa się również odwrotność, Ponieważ odwrotność multiplikatywna jest uzyskiwana przez wymianę licznika i mianownika, na przykład multiplikatywna odwrotność 3/4 wynosi 4/3.
Zasadniczo można powiedzieć, że dla liczby racjonalnej (P/Q) Twoja multiplikatywna odwrotność (P/Q)-1 To wzajemne (Q/P) Jak można zweryfikować poniżej:
(P/Q) ⋅ (P/Q)-1 = (p/q) ⋅ (q/p) = (p⋅ q)/(q⋅ p) = (p⋅ q)/(p⋅ q) = 1
Odwrotność multiplikatywna nie istnieje w zestawie liczbowym liczb całkowitych, Na przykład, jeśli cała liczba 2 zostanie pobrana, jego multiplikatywna odwrotność według tego, co było widoczne powyżej, wynosiłaby ½, ale ½ nie jest liczbą całkowitą.
Istnieje również multiplikatywna odwrotność elementu zerowego mnożenia. Innymi słowy, liczba zerowa (0), która jest elementem zerowym operacji mnożenia, nie ma odwrotności multiplikatywnej, ponieważ nie ma liczby mnożonej przez zero urządzenia.
Multiplikatywna odwrotność istnieje w liczbach racjonalnych, w liczbach rzeczywistych i liczbach złożonych.
Multiplikatywne przykłady odwrotne
Przykład 1
Znajdź 3/2 multiplikatywny odwrotność i sprawdź, czy spełnia własność liczb całkowitych multiplikatywnych.
Może ci służyć: Koplanares Punkty: Równanie, przykład i rozwiązane ćwiczeniaZgodnie z powyższą zasadą, multiplikatywna odwrotność (3/2) jest (2/3) jest wymieniana w ten sposób. Aby zweryfikować mnożenie dwóch liczb:
(3/2) ⋅ (2/3) = (3 ⋅ 2)/(2 ⋅ 3) = 6/6 = 1.
Aby pomnożyć dwie liczby ułamkowe, po prostu pomnoż licznik pierwszego przez drugi licznik, aby uzyskać licznik wyników.
Aby uzyskać mianownik produktu o liczbie ułamkowej, postępuj w podobny sposób, to znaczy mianowniki są mnożone ze sobą, a wynik jest mianownik produktu. W naszym przykładzie zweryfikuje się, że licznik iloczyn liczby i jego wzajemny wynosi 6, a mianownik to 6, pozostawiając ułamek 6/6, który wynosi 1.
Przykład 2
Multiplikatywną odwrotność -5 nie należy mylić z jego symetrycznym (+5), który czasami nazywany jest odwrotnością arytmetyczną. Odwrotność multiplikatywna zostanie uzyskana w następujący sposób:
(-5) ⋅ x = 1
Gdzie x jest multiplikatywną odwrotnością, którą należy uzyskać. Możliwa procedura polega na oczyszczeniu nieznanego x. Jak (-5) mnoży nieznany x w lewym członku, dzieje się to dzieląc prawego członka:
X = 1 / (-5)
Jak wiadomo, że + między - to - w końcu otrzymuje X:
X = - ⅕ .
Podsumowując - ⅕ jest multiplikatywną odwrotnością -5.
Przykład 3
Uzyskaj multiplikatywną odwrotność √2. Załóżmy, że multiplikatywna odwrotność to x, a następnie -√2 pomnożone przez x musi być jednostką, warunkiem, który narzucamy poniżej:
-√2 ⋅ x = 1
Obaj członkowie są podzielone przez √2, aby uzyskać:
(--√2 ⋅ x) / (-2.2) = 1 / (√2)
Pierwszy członek jest uproszczony -„Pozostałe:
Może ci służyć: standardowy błąd oceny: jak jest obliczany, przykłady, ćwiczeniaX = 1 / (--√2)
To wyrażenie może być zracjonalizowane, to znaczy eliminowanie korzenia mianownika, mnożąc licznik przez (-√2) i w mianowniku dla tej samej kwoty, aby wynik nie został zmieniony:
X = (-√2) / [(-√2) (-√2)] =-(√2 / 2)
Podsumowując - (√2/2) to odwrotność multiplikatywna (√2).
Przykład 4
Załóż dowolną liczbę X, zdobądź odwrotność multiplikatywną i reprezentuj ją graficznie.
W takim przypadku jest to funkcja f (x) = x, uzyskiwanie odwrotności multiplikatywnej jest znalezienie funkcji g (x), tak że pomnożone przez pierwszą jednostkę urządzenia. Funkcja G jest wzajemną funkcją F i nie należy w żaden sposób mylić z jej funkcją odwrotną.
Innymi słowy, multiplikatywna odwrotność x jest a taka, że następujące są spełnione:
x ⋅ y = 1
Gdzie oczyścić i mieć:
y = 1/x.
Powyższe jest interpretowane w ten sposób, biorąc pod uwagę wartość x, poprzedni wzór daje nam jego multiplikatywną odwrotność.
Możliwe jest utworzenie reprezentacji graficznej, jak pokazano na poniższym rysunku:
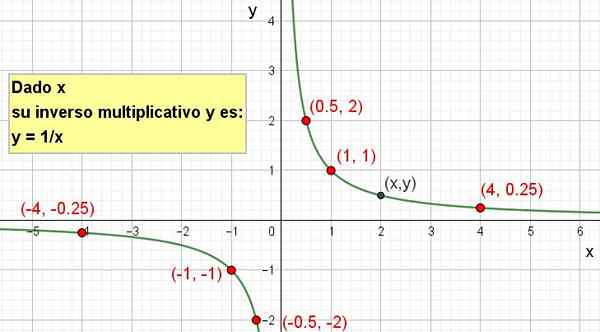 Rysunek 2. Multiplikatywna odwrotność x wynosi y = 1/x.
Rysunek 2. Multiplikatywna odwrotność x wynosi y = 1/x. Ćwiczenia
Ćwiczenie 1
Biorąc pod uwagę x = 2 - √2, zdobądź multiplikatywną odwrotność i.
Rozwiązanie:
Tak i jest to multiplikatywny x x
x ⋅ y = 1
X jest zastąpiony jego wartością:
(2 - √2) ⋅ y = 1
Potem to oczyści i:
y = 1 / (2 - √2)
Racjonalizacja wyniku mnoży licznik i mianownik przez jego sprzężony dwumian:
y = (2 + √2) / ((2 + √2) (2 - √2))
W mianowniku rozpoznawano godny znaczący produkt nazywany produktem suma dla różnicy, która jest różnicą kwadratów. W ten sposób korzeń znika w mianowniku.
y = (2 + √2) / (2^2 - (√2)^2)
Może ci służyć: proporcjaRozwiązanie mocy:
y = (2 + √2) / (4 - 2)
Uproszczenie:
y = (2 + √2) / 2
Ćwiczenie 2
Uzyskaj odwrotność multiplikatywną (1/a + 1/b), gdzie A i B są różnymi liczbami rzeczywistymi.
Rozwiązanie:
Nazywamy i multiplikatywną odwrotność (1/a + 1/b), aby musiało zostać spełnione następujące równanie:
I ⋅ (1/a + 1/b) = 1
Zmienna jest wyczyszczona i:
Y = 1/(1/a + 1/b)
Mianownik jest rozwiązany:
Y = 1 / ((b + a) / a b)
Jak wiadomo o zasadach algebry, mianownik mianownika przechodzi do licznika:
Y = (a b) / (b + a)
Nakazuje się w końcu uzyskać:
(A B)/(A + B), który jest multiplikatywną odwrotnością (1/A + 1/B).
Ćwiczenie 3
Uzyskaj multiplikatywną odwrotność (a - b) / (a^2 - b^2).
Rozwiązanie:
Przypomnijmy, że odwrotność multiplikatywna jest również nazywana wzajemną, ponieważ jest uzyskiwana po prostu wymieniając licznik i mianownik.
Wówczas multiplikatywna odwrotność (a - b) / (a^2 - b^2) będzie:
(A^2 - b^2) / (a - b)
Ale to wyrażenie można uprościć, jeśli rozpoznajemy, zgodnie z regułami algebry, że licznik jest różnicą kwadratów, które mogą być faktoringowe jako iloczyn sumy dla innej różnicy:
((A + b) (a - b)) (a - b)
Ponieważ istnieje wspólny czynnik (a - b) w licznikach i w mianowniku przystępujemy do uproszczenia, ostatecznie uzyskując:
(A + B), który jest odwrotną multiplikatywną (A - B) / (A^2 - B^2).
Bibliografia
- Źródła, a. (2016). PODSTAWOWA MATEMATYKA. Wprowadzenie do obliczeń. Lulu.com.
- Garo, m. (2014). Matematyka: równania kwadratowe: jak rozwiązać równanie kwadratowe. Marilù Garo.
- Haeussler, e. F., I Paul, r. S. (2003). Matematyka administracji i ekonomii. Edukacja Pearsona.
- Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Matematyka 1 września. Próg.
- Precious, c. T. (2005). Kurs matematyki 3o. Progreso redakcyjne.
- Rock, n. M. (2006). Algebra I jest łatwa! Tak łatwo. Team Rock Press.
- Sullivan, J. (2006). Algebra i trygonometria. Edukacja Pearsona.

