Definicja hiperkubu, wymiary, współrzędne, rozwinięte

A Hyperkubo to kostka wymiaru n. Konkretny przypadek wymiaru Hyperkubo jest nazywany Testeract. Hiperkub lub N-cubo składa się z prostych segmentów, o tej samej długości, które są ortogonalne w ich wierzchołkach.

Ludzie postrzegają trzy -wymiarową przestrzeń: szeroka, wysoka i głębokość, ale nie jest możliwe wizualizację hiperkubu wymiaru większego niż 3. 

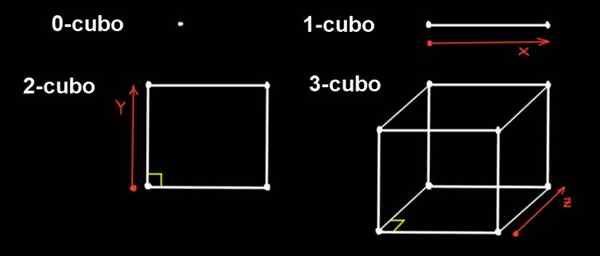
Rysunek 1. 0-CUBO jest punktem, jeśli ten punkt rozciąga się w jednym kierunku w odległości 1-kubo, jeśli ten 1-cubo rozciąga się odległość do ortogonalnego kierunku, istnieje 2-cubo (z boków do x a), Jeśli 2-CUBO rozciąga się w kierunku ortogonalnym, istnieje 3-cubo. Źródło: f. Zapata.

Możemy wykonać projekcje w trzy -wymiarowej przestrzeni, aby ją reprezentować, podobnie jak w sposób, w jaki projektujemy kostkę w samolocie, aby ją reprezentować.

W wymiarze 0 jedyną liczbą jest punkt, więc 0-cubo jest punktem. 1-cubo to segment prosty, który powstaje przez przesuwanie punktu w odległości do odległości do.

Ze strony 2-cubo to kwadrat. Jest zbudowany przez wypieranie 1-cubo (odcinka długości a) w kierunku i, który jest ortogonalny do adresu x, odległość do.

3-CUBO to wspólna kostka. Jest zbudowany z kwadratu wypierającego to samo w trzecim kierunku (z), który jest ortogonalny do kierunków x i y, odległość Do.

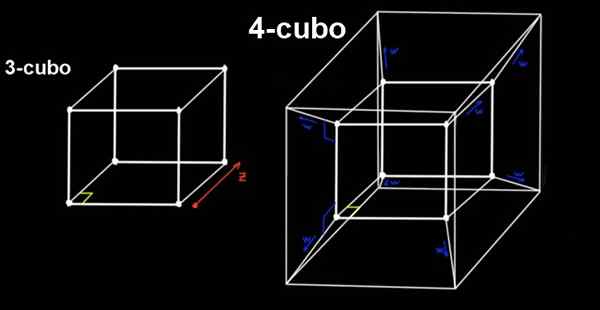Rysunek 2. 4-cubo (testerakt) to rozszerzenie 3-cubo w kierunku ortogonalnym do trzech konwencjonalnych adresów przestrzennych. Źródło: f. Zapata.

4-CUBO to próba, która jest zbudowana z 3-cubo wypierającego to samo ortogonalnie, odległość Do, w kierunku czwartego wymiaru (lub czwartego kierunku), którego nie możemy dostrzec.

Spust ma wszystkie swoje proste kąty, ma 16 wierzchołków i wszystkie jego krawędzie (łącznie 18) mają taką samą długość Do.

Jeśli długość krawędzi N-cubo lub hiperkubo wymiaru n wynosi 1, to jest to jednostka hiperkubowa, w której najdłuższe miary przekątne √n √n √n.

Może ci służyć: programowanie liniowe: do czego to jest modele, ograniczenia, aplikacjeRysunek 3. N-cubo jest uzyskiwane z (n-1) -Cubo rozszerzającego go ortogonalnie w następnym wymiarze. Źródło: Wikimedia Commons.

[TOC]

Jakie są wymiary?

Wymiary to stopnie swobody lub możliwe kierunki, w których obiekt może się poruszać.

W wymiarze 0 nie ma możliwości poruszania się, a jedynym możliwym obiektem geometrycznym jest punkt.

Wymiar w przestrzeni euklidowskiej jest reprezentowany przez linię zorientowaną lub osą, która określa ten wymiar, zwany oś x. Oddzielenie dwóch punktów A i B jest dystansem euklidowskim:

D = √ [(x_Do - X_B)²]. 

W dwóch wymiarach przestrzeń jest reprezentowana przez dwie ortogonalne linie zorientowane na siebie, zwane x i osi.

Pozycja dowolnego punktu w tej dwuwymiarowej przestrzeni jest podawana przez parę współrzędnych kartezjańskich (x, y) i odległość między dwoma punktami a i b, każde będzie:

D = √ [(x_Do - X_B)² + (I_Do - I_B)²]

Ponieważ jest to przestrzeń, w której geometria euklii.

Trzy -wymiarowa przestrzeń

Trzy -wymiarowa przestrzeń to przestrzeń, w której się poruszamy. Ma trzy kierunki: szerokość, wysoka i głębokość.

W pustym pokoju prostopadłe zakątki dają te trzy kierunki i każdemu z nich możemy powiązać oś: x, y, z.

Ta przestrzeń jest również euklidowski, a odległość między dwoma punktami A i B jest obliczana w następujący sposób:

D = √ [(x_Do - X_B)² + (I_Do - I_B)² + (z_Do - z_B)²]

Ludzie nie mogą dostrzec więcej niż trzech wymiarów przestrzennych (lub eukliideas).

Jednak z ściśle matematycznego punktu widzenia jest to możliwe.

W tej przestrzeni punkt ma współrzędne: (x1, x2, x3, ..., xn), odległość między dwoma punktami to: 

D = √ [(x_1st - X_{1 b})² + (X₂ - X_2b)² +... + (x_na - X_NB)²].

Może ci służyć: rozkład hipergeometryczny: wzory, równania, model

Czwarty wymiar i czas

Rzeczywiście, w teorii czasu względności jest traktowane jako jeden jeszcze wymiar, a współrzędna jest powiązana.

Ale należy wyjaśnić, że ta współrzędna powiązana z czasem jest liczbą wyimaginowaną. Dlatego oddzielenie dwóch punktów lub wydarzeń w czasie przestrzeni nie jest Euclidiana, ale podąża za miarą Lorentz.

Czterowymiarowy hiperkub (spust) nie żyje w czasie kosmosu, należy do czterowymiarowej hiper-przestrzeni eukliidealnej. 

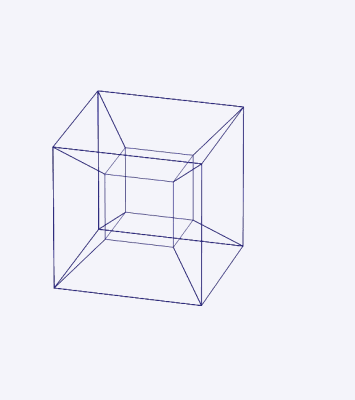
Rysunek 4. Projekcja 3D czterodwozimnego hiperkubu w prostym obrotu wokół płaszczyzny, która dzieli przednią figurę po lewej, z powrotem na prawą i od góry do dołu. Źródło: Wikimedia Commons.

Współrzędne hiperkubu

Współrzędne wierzchołków N-cubo skoncentrowanego na pochodzeniu są osiągane poprzez uczynienie wszystkich możliwych permutacji następującego wyrażenia:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Gdzie A jest długością krawędzi.

-On tom Z krawędzi krawędzi A to: (A/2)^N (2^N) = a^N.

- Najdłuższy przekątna Jest to odległość między przeciwnymi wierzchołkami.

-Oto następujące przeciwne wierzchołki na placu: (-1, -1) i (+1, +1).

-I w Sześcian: (-1, -1, -1) i (+1, +1, +1). 

- Najdłuższy przekątna miar N-Cubo: 

D = √ [1 -(-1))² +… + (1 -(-1))²] = √ [n 2²] = 2√n

W tym przypadku założono, że strona wynosi a = 2. Po stronie N-Cubo dla każdego pozostanie:

d = a√n.

-Próba ma każdy z 16 wierzchołków podłączony do czterech krawędzi. Poniższy rysunek pokazuje, w jaki sposób wierzchołki są podłączone do spustu.

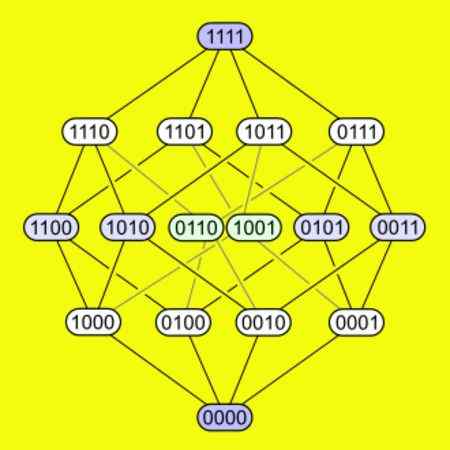Rysunek 5. Pokazano 16 wierzchołków czterech wymiarowych hiperkubów i jak łączą się to samo. Źródło: Wikimedia Commons.

Rozkoszował się hiperkubu

Regularną figurę geometryczną, na przykład wielościan, można rozwinąć w kilku figurkach o niższej wymiaru.

W przypadku 2-cubo (kwadrat) można rozwinąć w czterech segmentach, to znaczy cztery 1-cubo.

Może ci służyć: rozkład Poissona: wzory, równania, model, właściwości

Podobnie 3-cubo można rozwinąć w sześciu 2-cubo.

Rysunek 6. N-cubo można rozwinąć w kilku (n-1) -Cubos. Źródło: Wikimedia Commons.

4-cubo (testeract) można rozwinąć w ośmiu 3-cubo.

Poniższa animacja pokazuje rozwijanie faki.

Rysunek 7. 4 -wymiarowe hiperkubo można rozwinąć w ośmiu trzech kostkach wymiarowych. Źródło: Wikimedia Commons. Cyfra 8. Trzy -wymiarowa projekcja czterech wymiarowych hiperkubów, wykonując podwójną obrót wokół dwóch płaszczyzn ortogonalnych. Źródło: Wikimedia Commons.

Bibliografia

1. Kultura naukowa. Hyperkubo, wizualizacja czwartego wymiaru. Pobrano z: CultuRacientifica.com
2. Epsilones. Tetradimensional Hyperkubo lub Tesseract. Odzyskane z: epsilones.com
3. Perez R, Aguilera A. Metoda uzyskania badania z rozwoju hiperkubu (4D). Odzyskane z: badań.internet
4. Wikilibros. Matematyka, wielościan, hiperkube. Odzyskane z: jest.Wikibooks.org
5. Wikipedia.  Hypercube. Źródło: w:.Wikipedia.com
6. Wikipedia. Tesseract. Źródło: w:.Wikipedia.com