Gravicentro

Jaki jest podatek?

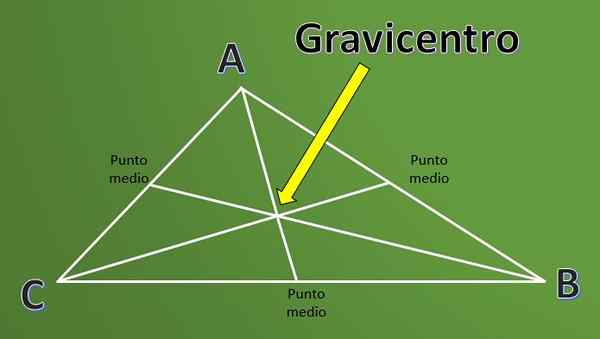
On Gravicentro Jest to definicja, która jest szeroko stosowana w geometrii podczas pracy z trójkątami. Aby zrozumieć definicję Gravicentro, najpierw konieczne jest znanie definicji „medium” trójkąta.

Mediany trójkąta to segmenty linii, które zaczynają się od każdego wierzchołka i docierają do punktu środkowego przeciwnej strony do wspomnianego wierzchołka.

Punkt przecięcia trzech median trójkąta nazywa. Nie wystarczy po prostu poznać definicję, interesujące jest wiedzieć, w jaki sposób ten punkt jest obliczany.

Obliczanie barów

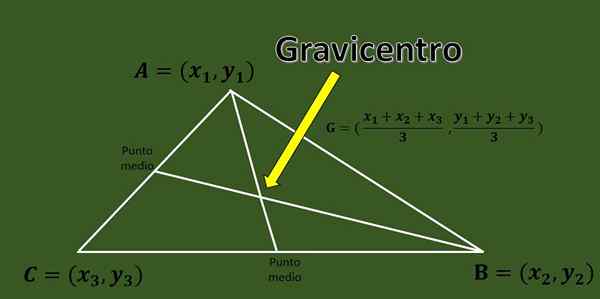
Biorąc pod uwagę trójkąt ABC z wierzchołkami a = (x1, y1), b = (x2, y2) i c = (x3, y3), Gravicentro jest przecięciem trzech median trójkąta trójkąta.

Szybka formuła, która umożliwia obliczenie opodatkowania trójkąta, współrzędne jego wierzchołków znane jest:

G = ((x1+x2+x3)/3, (y1+y2+y3)/3).

Dzięki tej formule możesz znać lokalizację gravicentro w płaszczyźnie kartezjańskiej.

Charakterystyka podatku

Nie jest konieczne śledzenie trzech median trójkąta, ponieważ podczas rysowania dwóch z nich zostanie dowodem, gdzie jest podatkowanie.

Opodatkowanie dzieli każdą medianę na 2 części, których odsetek wynosi 2: 1, to znaczy, że dwa segmenty każdej mediany są podzielone na segmenty długości 2/3 i 1/3 długości całkowitej, a większa odległość to jedna istnieje jedna istnieje jedna odległość co jest między wierzchołkiem a ulotką.

Poniższy obraz ilustruje tę właściwość lepiej.

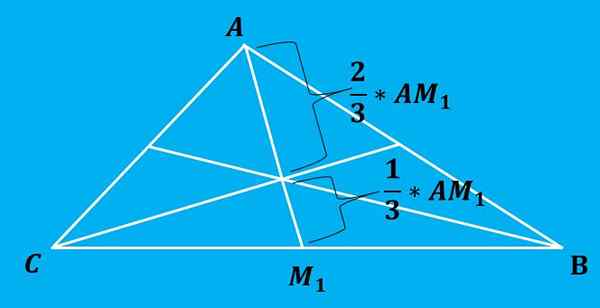
Formuła obliczania opodatkowania jest bardzo prosta do zastosowania. Sposobem na uzyskanie tego wzoru jest obliczenie równań prostych, które definiuje każda mediana, a następnie znalezienie punktu cięcia tych linii.

Ćwiczenia

Poniżej znajduje się niewielka lista problemów dotyczących obliczania barucznika.

1.- Biorąc pod uwagę trójkąt wierzchołków A = (0,0), B = (1,0) i C = (1,1), oblicz opodatkowanie wspomnianego trójkąta.

Za pomocą danego wzoru można szybko stwierdzić, że grawiciastro trójkąta ABC to:

G = ((0+1+1)/3, (0+0+1)/3) = (2/3, 1/3).

2.- Jeśli trójkąt ma wierzchołki a = (0,0), b = (1,0) i c = (1/2.1), jakie są współrzędne opodatkowania?

Ponieważ znane są wierzchołki trójkąta, stosuje się wzór do obliczenia opodatkowania. Dlatego Gravicentro ma współrzędne:

G = ((0+1+1/2)/3, (0+0+1)/3) = (1/2, 1/3).

3.- Oblicz możliwych podatników dla trójkąta równobocznego, tak że dwa z jego wierzchołków to A = (0,0) i B = (2,0).

W tym ćwiczeniu określane są tylko dwa wierzchołki trójkąta. Aby znaleźć możliwe grawitacje, trzeci wierzchołek trójkąta musi najpierw obliczyć.

Ponieważ trójkąt jest równoboczny, a odległość między A i B wynosi 2, trzeci wierzchołek C musi znajdować się w odległości 2 A i B.

Korzystając z faktu, że w trójkącie równobocznym wysokość pokrywa się z medianą, a także za pomocą twierdzenia Pitagorasa, można stwierdzić, że opcje współrzędnych trzeciego wierzchołka wynoszą C1 = (1, √3) lub C2 = (1, - - - √3).

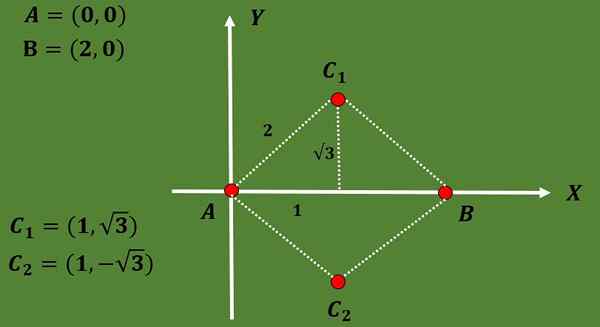
Tak, aby współrzędne dwóch możliwych grawitacji to:

G1 = ((0+2+1)/3, (0+0+√3)/3) = (3/3, √3/3) = (1, √3/3),

G2 = ((0+2+1)/3, (0+0 --√3)/3) = (3/3, -√3/3) = (1, √3/3).

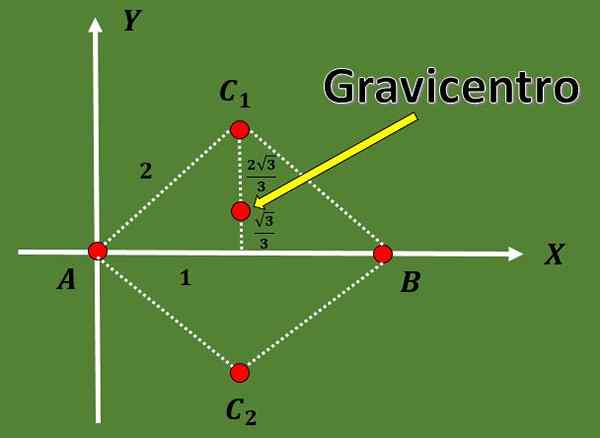
Dzięki poprzednim relacji można również zauważyć, że mediana jest podzielona na dwie części, których odsetek wynosi 2: 1.