Geometria analityczna

Wyjaśniamy, jaka geometria analityczna, jej historia, jakie są badania i zastosowania

Co to jest geometria analityczna?

Geometria analityczna Jest to gałąź matematyki, w której geometria i algebra są łączone, aby rozwiązać różne problemy geometryczne za pomocą technik algebraicznych.

Użyj układów współrzędnych, takich jak kartezjański układ współrzędnych, który zawdzięcza swoją nazwę René Descartes. W ten sposób można kojarzyć krzywe w płaszczyźnie i w przestrzeni, z równaniami algebraicznymi.

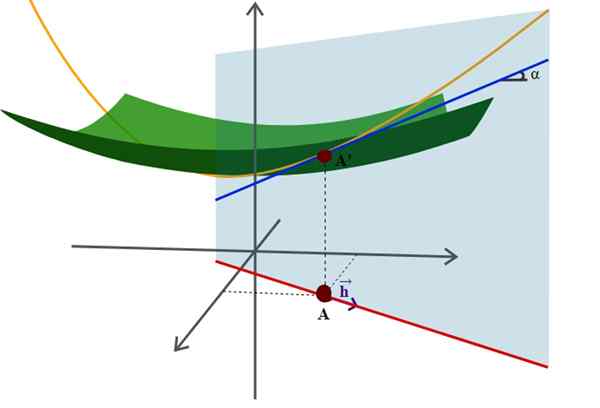
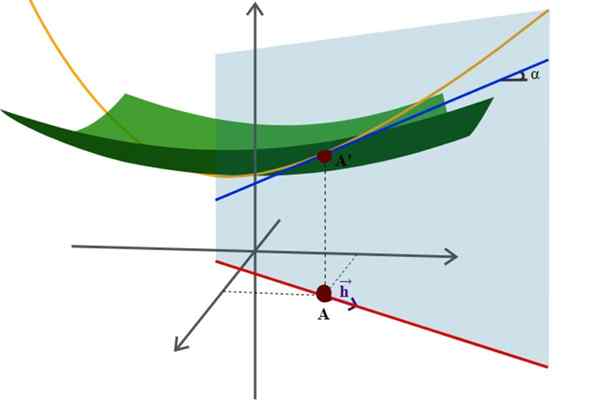Schemat powierzchni w przestrzeni i jej kierunkowej pochodnej, jedno z wielu bardziej zaawansowanych zastosowań geometrii analitycznej. Źródło: Wikimedia Commons.

Przykładem tego jest dobrze znane równanie R -Riortion o promieniu wyśrodkowanym na pochodzeniu układu współrzędnych:

Niewątpliwie w wielu przypadkach łatwiej jest pracować z algebraiczną ekspresją krzywej, niż z samą jej geometryczną reprezentacją. Dzieje się tak przy obliczaniu skrzyżowań między krzywych lub znajdując do nich linie styczne lub suszenia.

Podobnie, poprzez geometrię analityczną, możliwe jest układanie grafiki. I, jak wiadomo, funkcje umożliwiają modelowanie problemów naukowych i inżynierskich. Dlatego geometria analityczna występuje w programach nauczania kariery związanych z tymi obszarami wiedzy.

Krótka historia geometrii analitycznej

Geometria analityczna ma swoje pochodzenie w pierwszej połowie XVII wieku, z ręki dwóch znanych francuskich matematyków: René Descartes (1596-1650) i Pierre de Fermat (1601-1665).

Rene Descartes

Można jednak powiedzieć, że jego pochodzenie sięgają stuleci, do greckiego matematyka Apolloniusa z Pergamo (262-190 a.C.). Napisał traktat o stożku, do którego przyznał ich nazwiska: obwód, elipsa, przypowieść i hiperbola.

Może ci służyć: proporcjonalność złożona: wyjaśnienie, trzy złożone reguły, ćwiczenia

Zatem praca Apollonio była podstawą, znacznie później, francuski René Descartes i Pierre de Fermat położył fundamenty geometrii analitycznej, niezależnie. Ale Kartezjusz jest uważany za ojca tej nauki, ponieważ jako pierwszy opublikował swoje prace.

Kartezjusz, Fermat i Euler

W mowie metody 1637 Kartezjusz zjednoczył dwie dyscypliny, które do tej pory zostały oddzielone: ​​algebra i geometria. W swojej pracy Descartes wprowadza kartezjański układ współrzędnych, aby zlokalizować punkty w samolocie i w przestrzeni.

Wykorzystuje również równania algebraiczne drugiego stopnia z dwiema zmiennymi, do opisania sekcji stożkowych i jest dedykowana do rozwiązywania z nimi problemów geometrycznych. Także w celu stworzenia znacznej części notacji matematycznej, która jest obecnie używana.

Pierre de Fermat jest bardziej związany z optyką niż z geometrią analityczną, jednak ich wkład jest godny uwagi.

W 1629 r Miejsce geometryczne, z którym rozpoczyna się badanie geometrii analitycznej.

Jednak prace Fermata nie widziały światła dopiero w 1679 r., Opublikowane przez jego syna, kiedy matematyk już zmarł. Z tego powodu ojcostwo geometrii analitycznej przypisuje się Kartezjuszowi.

Następnie do francuskich matematyków szwajcarski Leonardo Euler (1707-1783) ustanowił formalne podstawy geometrii analitycznej. Euler wprowadził kilka układów współrzędnych w płaszczyźnie i przestrzeni: współrzędne prostokątne, polarne i ukośne, a także transformacje z jednego systemu na drugi.

Może ci służyć: w jaki sposób informacje są uzyskane w ankiecie?

W swoich pracach na temat geometrii analitycznej Euler pogłębił również klasyfikację różnych krzywych, zgodnie ze stopniem reprezentatywnego równania algebraicznego (trzeci i czwarty rzęd więcej.

Jakie badania geometria analityczna?

Ogólnie rzecz biorąc, geometria analityczna koncentruje się na badaniu elementów geometrycznych, takich jak punkty, segmenty, linie, krzywe, powierzchnie i objętości. Aby to zrobić, jak wspomniano powyżej, ustanawia równania algebraiczne, które opisują i odnoszą te elementy, umożliwiając ich zarządzanie za pomocą technik algebraicznych.

Główne cele geometrii analitycznej, w bardzo podsumowujący sposób, są następujące:

1. Ustal kartezjański układ współrzędnych i układ współrzędnych polarnych, aby zlokalizować punkty w płaszczyźnie, a także jego rozszerzenie do punktów w przestrzeni.
2. Narysuj segmenty, proste, krzywe i powierzchnie na płaszczyźnie i przestrzeni kartezjańskiej.
3. Wydedukuj równania, które analitycznie opisują krzywą i budowę jej w płaszczyźnie i/lub przestrzeni, a także badanie wszystkich jego właściwości.
4. Klasyfikuj krzywe, powierzchnie i objętości.
5. Wyposaż podstawowe formuły w celu rozwiązywania problemów na godnych uwagi punktów, prostych, planach, kątach, równoległości, prostopadłości, odległościach, skrzyżowaniach, obszarach i innych.
6. Rozwiąż problemy geometryczne poprzez zastosowanie metod algebraicznych, dla których wzory odnoszące się do godnych uwagi punktów, równania dla linii, planów, kąty, odległości między punktami i punktami, punktami stycznymi, suchymi liniami, obszarami, obszarami i wiele więcej.
7. Pracuj z przestrzeniami wektorowymi i produktami między wektorami.

Odległość między dwoma punktami

Jako przykład licznych zastosowań geometrii analitycznej, jednym z najprostszych jest obliczenie odległości między dwoma punktami płaszczyzny. Są dwa punkty P₁ I p₂, współrzędnych (x₁,I₁) i (x₂,I₂) odpowiednio, odległość d między nimi jest obliczana przez:

Może ci służyć: trójmian

Współrzędne polarne

Punkt płaszczyzny można określić przez jego odległość „R” do pochodzenia układu współrzędnych, zwanego polo, oraz kąt, który tworzy linię zawierającą do punktu i bieguna, z osą poziomą lub osą polarną.

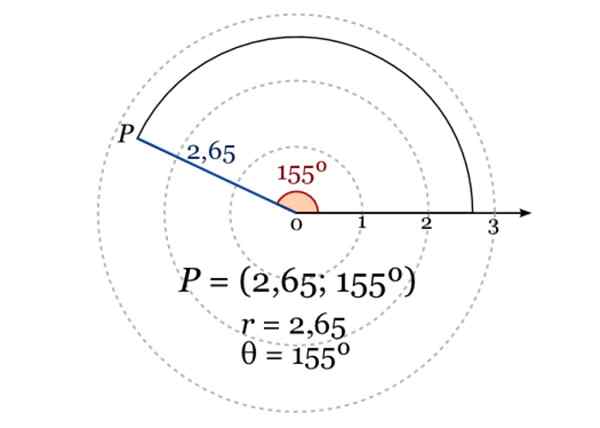Obraz pokazuje współrzędne polarne punktu P, gdzie r = 2.65, a kąt w stopniach w odniesieniu do osi polarnej wynosi 155º. Źródło: Wikimedia Commons.

Zastosowania geometrii analitycznej

Podstawa obliczeń nieskończenie małej

Geometria analityczna jest niezbędna do opracowania obliczeń nieskończenie małej, ponieważ ułatwia graficzną reprezentację krzywych i funkcji oraz działa z nimi w sposób analityczny, aby stworzyć modele reprezentujące zjawisko natury.

Mapy

Kartezjański układ współrzędnych pomaga tworzyć mapy i identyfikować miejsca poprzez szerokość i długość, równoważne współrzędne kartezjańskie punktu w płaszczyźnie.

Obliczenia topograficzne

Różne rodzaje układów współrzędnych są wykorzystywane w topografii i stanowią podstawę ich badań i zastosowań. Wśród nich jest polarny układ współrzędnych opisany powyżej.

Trajektorie ciał niebieskich

Skrawki stożkowe, opisane przez geometrię analityczną, uczestniczą w ważnych zjawiskach natury, takich jak trajektorie ciał niebieskich, z zastrzeżeniem siły grawitacji. Na przykład planety i niektóre komety opisują eliptyczne trajektorie wokół słońca, a to znajduje się w jednym z reflektorów.

Architektura i konstrukcje cywilne

Na przykład wiele krzywych jest częścią konstrukcji architektonicznych, kable wiszącego mostu mogą przybierać formę przypowieści.

Globalne systemy pozycjonowania

Globalny system pozycjonowania lub GPS umożliwia możliwe lokalizacje z precyzją, a także poruszające się obiekty, takie jak pojazdy i łodzie. Pomaga także ludziom łatwiej dotrzeć do swoich miejsc docelowych, prowadząc ich na najlepszych trasach.