Matematyka

Funkcje wektora

585
103
Eliasz Dubiel

Jakie są funkcje wektorowe?

A funkcja wektora parametru T, Jest to funkcja, której domena są prawdziwymi wartościami T, podczas gdy trasa jest tworzona przez wektory formy R (T). Taka funkcja można wyrazić jako:

R (T) = f (T) Siema + G (T) J + H (T) k

Gdzie Siema, J I k Są to wektory jednostkowe w trzech głównych kierunkach przestrzeni, a funkcje F, G i H są rzeczywistymi funkcjami zmiennej T. Notacja wykorzystuje Bold, aby rozróżnić wielkości wektorowe.

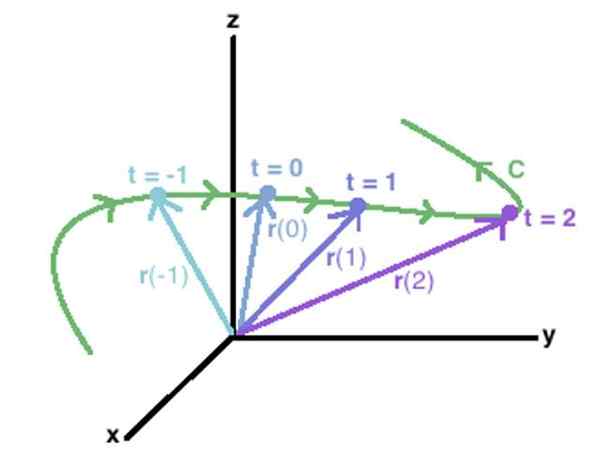Funkcję wektora w przestrzeni można użyć do opisania krzywej C, łącząc ekstremalne punkty każdego z wektorów określonych przez wspomnianą funkcję. Źródło: Wikidot.

Innym sposobem oznaczania funkcji wektorowej są nawiasy kwadratowe:

R (T) = T), G (T), H (T)>

Funkcje wektorowe można wykorzystać do badania krzywych w płaszczyźnie i przestrzeni, takich jak trajektoria, która podąża za ruchomym obiektem. Przykładem jest przypowieść opisana przez rzutowaną piłkę z początkową prędkością, pod grawitacją.

Jeśli chcesz poznać pozycję piłki w każdej chwili T, Funkcja wektora z dwoma komponentami, jednym poziomym i jednym pionowym:

R (T) = x (T) Siema + I(T) J

Oba x (T) jak y (T) Są funkcjami czasowymi T. Zatem przy dołączaniu do ekstremalnych punktów każdego z wektorów R(T) Możliwe, uformuj przypowieść opisaną przez piłkę w płaszczyźnie Xy.

Koncepcja łatwo rozciąga się na krzywą C w przestrzeni, na przykład ta pokazana na powyższym rysunku. Pojawiają się w nim wektory R (-1), R (0), R (1) R (2), których końce narysują krzywą C, narysowane na zielono.

Limity, pochodne i całka funkcji wektorowych

Narzędzia obliczeniowe mające zastosowanie do rzeczywistych funkcji zmiennych rzeczywistych można również zastosować do funkcji wektorowych.

Może ci służyć: czynnikowanie

Limit funkcji wektorowej

Limit funkcji wektora R (T) = f (T) Siema + G (T) J + H (T) k, Gdy t → a, jest to zdefiniowane jako:

$\dpi110 \displaystyle \lim_t \to a\textbfr(t)=\left [ \displaystyle \lim_ t\to a f(t)\right ]\textbfi+\left [ \displaystyle \lim_ t\to a g(t)\right ]\textbfj+\left [ \displaystyle \lim_ t\to a h(t)\right ]\textbfk$

Zakładając, że istnieją odpowiednie granice F (T), G (T) i H (T), Kiedy T → a.

Pochodzący z funkcji wektorowej

Definicja pochodzenia z funkcji wektorowej R (t) = f (T) Siema + G (T) J + H (T) k Jest analogiczny do funkcji pochodnej rzeczywistej funkcji zmiennej rzeczywistej. Powołanie R„(t) do wspomnianej pochodnej, masz:

$\dpi110 \mathbfr'(t)=\displaystyle \lim_\Delta t \to 0\frac\mathbfr(t+\Delta t)-\mathbfr(t)\Delta t$

Pochodna istnieje, gdy istnieje poprzedni limit, a jeśli tak, funkcja R(T) jest zróżnicowany w T.

Integral funkcji wektorowej

Być R (t) = f (T) Siema + G (T) J + H (T) k funkcja wektorowa, taka, że funkcje F, G i H są zintegrowane w T.

Więc:

$\dpi110 \int \mathbfr(t)dt =\left [ \int f(t)dt \right ]\mathbfi+\left [ \int g(t)dt \right ]\mathbfj+\left [ \int h(t)dt \right ]\mathbfk+\mathbfC$

C = c₁Siema + C₂J

Co oznacza, że stała integracji jest również wektorem, ale stała.

Przykłady funkcji wektora

Przykład 1

Masz funkcję wektora podaną przez R (T) = 3Sec T Siema + 2Tan T J. Możliwe jest ocenę go pod kątem różnych wartości t, takich jak t = π/4 i t = π, co daje wektory R (π/4) i R (π):

R (π/4) = 3sec (π/4) Siema + 2Tan (π/4) J = 3√2 Siema + 2 J

R (π) = 3sec (π) Siema+2Tan (π) J = - 3 Siema

Jednakże, R (T) Nie istnieje dla wartości t = ∓π/2, ∓3π/2, ∓5π/2…, ponieważ funkcja SEC T = 1 /cos T Nie jest zdefiniowane, czy to tak T = Sen T / cos T.

Dlatego domeną funkcji r (t) jest wszystkie rzeczywiste wartości t, z wyjątkiem wartości:

∓ (2n+1) π/2; Z n = 0, 1, 2, .. .

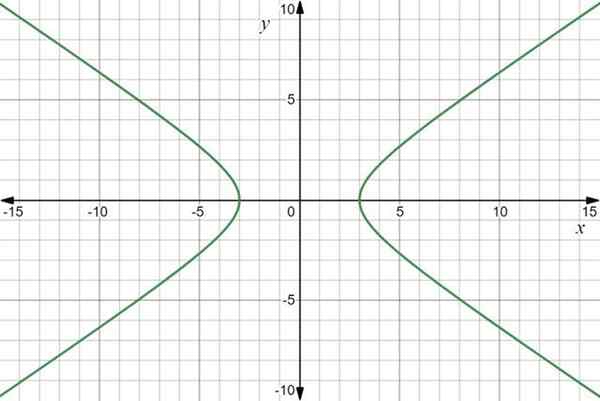
Wykres funkcji to hiperbola:

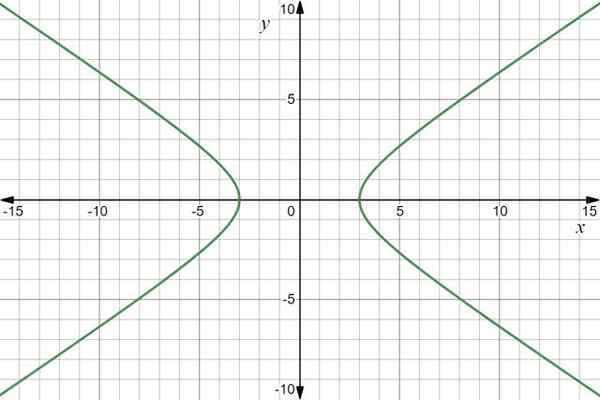Wykres funkcji wektora R (t) = 3Sec t Siema+2 tan t J. Źródło: f. Zapata przez Desmos.

Przykład 2

W porzuceniu pocisku pozycja mobilna jest funkcją wektora R (T) = x (T) Siema + I(T) J . Zakładając, że odporność na powietrze nie interweniuje, a grawitacja jest jedyną siłą, która działa na telefon komórkowy, ruch poziome jest jednolite prostoliniowe, podczas gdy pionowy jest jednolicie przyspieszony, wynoszącym g = 9.8 m/s² Wartość przyspieszenia. To przyspieszenie jest pionowe w kierunku ziemi.

Może ci służyć: zasady pochodzenia (z przykładami)

W takim przypadku funkcje x (T) I (T) Są odpowiednio:

x (t) = x_albo + v_wół∙ t
i (t) = y_albo + v_Oy∙ t - ½ gt²

Kwoty v_wół i v_Oy Są to elementy funkcji wektora, która przez cały czas opisuje prędkość mobilną:

v (T) = v_X(T) Siema + v_I(T) J

v_wół = v_albo∙ cos θ
v_Oy = v_albo∙ Sen θ

Będąc θ kątem, który tworzy początkową prędkość w stosunku do poziomu.

Ze swojej części początkowa pozycja telefonu komórkowego jest punktem współrzędnym (x_albo,I_albo) lub równoważnie wektor pozycji podany przez:

R_albo (T) = x_albo Siema + I_albo J

Zauważ, że w pokazanych równaniach znak ujemny został przypisany do kierunku pionowego, więc trzeci termin równania dla y (t) przyjmuje go. Możliwe jest również przypisanie pochodzenia do początkowej pozycji telefonu komórkowego.

Natychmiastowa prędkość pocisku

Odwrotna prędkość v (t) jest pierwsza po pozycji, w odniesieniu do czasu. Oblicza się go poprzez zastosowanie znanych zasad pochodzenia:

v(t) = R ' (T) = [x (T) Siema + I(T) J]'= X '(T) Siema + I'(T) J = v_wółSiema + (v_Oy - GT) J

Moduł prędkości jest podany przez:

$\dpi110 \left|\textbfv \right|=\sqrtv_ox^2+v_oy^2$

Natychmiastowe przyspieszenie pocisku

Wiadomo, że jest to G, w kierunku pionowym i kierunku w dół. Jest to weryfikowane, wiedząc, że przyspieszenie jest pierwszą pochodną prędkości w odniesieniu do czasu (lub drugiej pochodnej pozycji w odniesieniu do czasu, jeśli jest preferowana):

Do(t) = V ' (T) = [V_wółSiema + (v_Oy - GT) J] '= [V_wółSiema] '+ [(v_Oy - GT) J] '= = - g J

Jest to właśnie oczekiwany wynik.

Ćwiczenie rozwiązane

Biorąc pod uwagę funkcję wektora R (T) = 3T Siema + (T - 1) J, znajdować R '(t) i R "(T).

Rozwiązanie

Stosując zasady wyprowadzania do każdego z komponentów, masz:

Może ci służyć: stała integracji: znaczenie, obliczenia i przykłady

R '(t) = = 3 Siema + J

A ponieważ pochodna stałej wynosi 0:

R "(t) = 0

To jest do powiedzenia, R "(t) jest równe wektorowi zerowej.

Bibliografia

Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
Larson, r. Obliczanie za pomocą geometrii analitycznej. 2. Wydanie. McGraw Hill.
Mathonline. Funkcje wektorowe. Odzyskane z: Mathonline.Wikidot.com.
Opentax. Rachunek Tom 3. Źródło: OpenStax.org.
Purcell, e. J. 2007. Obliczenie. Edukacja Pearsona.