Właściwości funkcji wykładniczych, przykłady, ćwiczenia

funkcja wykładnicza Jest to funkcja matematyczna o wielkim znaczeniu dla wielu aplikacji, które ma. Jest zdefiniowany w następujący sposób:

f (x) = b^X, Z B> 0 i B ≠ 1

Gdzie B jest prawdziwą stałą zawsze pozytywną i różnią się od 1, która jest znana jako baza. Zauważ, że prawdziwa zmienna X znajduje się w wykładnik potęgowy, W ten sposób f (x) jest zawsze liczbą rzeczywistą.

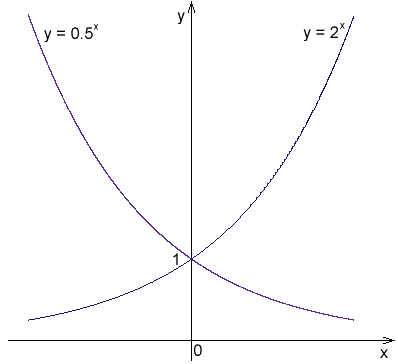Rysunek 1. Funkcje wykładnicze z podstawami 2 i 1/2

Przykłady funkcji wykładniczych są następujące:

-f (x) = 2^X

-g (x) = 5⋅E^-3x

-H (x) = 4⋅ (10^2x)

Są to funkcje, które rosną - lub zmniejszają się, zgodnie ze znakiem wykładnika - bardzo szybko, więc mówi się o „wzroście wykładniczym”, gdy pewna wielkość wzrasta bardzo szybko. Dlatego są one odpowiednie do modelowania wzrostu żywych istot, takich jak bakterie.

Kolejnym bardzo interesującym zastosowaniem jest zainteresowanie złożone. Im więcej pieniędzy masz na koncie, tym więcej odsetek i mogą one obliczać za każdym razem, gdy chcesz.

Za pomocą funkcji logarytmicznej, która jest odwrotną funkcją wykładniczą, może być wiadomo po tym, jak długo pewien kapitał wzrasta do określonej wartości.

[TOC]

Właściwości funkcji wykładniczych

Rysunek 2. Przykłady funkcji wykładniczych. Źródło: f. Zapata.

Poniżej znajdują się ogólne właściwości dowolnej funkcji wykładniczej:

-Wykres dowolnej funkcji wykładniczej zawsze przecina oś pionową w punkcie (0,1), jak można zobaczyć na rycinie 2. To dlatego, że b⁰ = 1 dla dowolnej wartości B.

-Funkcja wykładnicza nie przecina się na osi x, w rzeczywistości ta oś jest poziomą asymptotem dla funkcji.

-Od b¹ = b, punkt (1, b) zawsze należy do grafiki funkcyjnej.

Może ci służyć: pryzmat wątrobowy

-Domena funkcji wykładniczej jest zbiór liczb rzeczywistych i f (x) = b^X Jest ciągły w całej swojej domenie.

-Zakres funkcji wykładniczy.

-Funkcja wykładnicza jest jeden po drugim, to znaczy każda wartość X należąca do domeny funkcji, ma unikalny obraz w zestawie przyjazdu.

-Odwrotność wykładniczą jest funkcja logarytmiczna.

Poszczególne właściwości funkcji wykładniczych

Jak powiedzieliśmy wcześniej, funkcja wykładnicza może rosnąć lub zmniejszać.

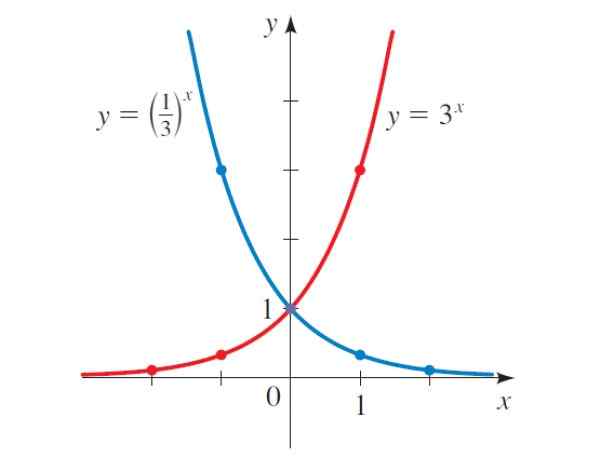
Jeśli wykres na ryc. 2 jest starannie zbadany, zauważa się, że jeśli b> 1, funkcja rośnie, na przykład y = 3^X, Ale w przypadku y = (1/3)^X, z B < 1, la función decrece.

Mamy dwa rodzaje funkcji wykładniczych z następującymi konkretnymi właściwościami:

Dla b> 1

-Funkcja zawsze rośnie.

-Gdy wartość B wzrasta, funkcja rośnie szybciej, na przykład y = 10^X rośnie szybciej niż y = 2^X.

-Gdy zmienna jest większa niż 0, funkcja uzyskuje wartości większe niż 1, to znaczy:

Dla x> 0: y> 1

-A jeśli x<0, entonces f(x) < 1.

Dla b < 1

-Funkcja zawsze maleje.

-Zmniejszając wartość B, funkcja zmniejsza się szybciej. Na przykład y = (1/5)^X zmniejsza się szybciej niż y = (1/3)^X.

-Dla wartości x niższe niż 0 funkcja przyjmuje wartości większe niż 1, to znaczy:

Dla x 1

-Wreszcie, gdy x> 0, wtedy i < 1.

Przykłady funkcji wykładniczych

Funkcja wykładnicza jest bardzo przydatna do modelowania zjawisk w nauce i gospodarce, jak zobaczymy poniżej:

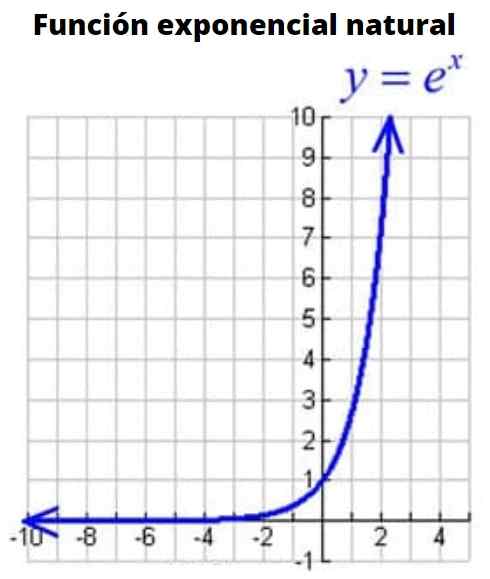
Naturalna funkcja wykładnicza

Rysunek 3: Naturalny wykres funkcji wykładniczy

Jest to funkcja, której podstawą jest liczba E lub liczba Eulera, liczba irracjonalna, której wartość to:

Może ci służyć: kąty uzupełniające: co to są, obliczenia, przykłady, ćwiczenia

E = 2.718181828…

Ta baza, nawet jeśli nie jest to okrągła liczba, działa bardzo dobrze w przypadku wielu aplikacji. Dlatego jest uważane za najważniejsze podstawy wszystkich funkcji wykładniczych. Naturalna funkcja wykładnicza jest wyrażana w sposób matematyczny jako:

f (x) = e^X

Funkcja wykładnicza często pojawia się w prawdopodobieństwie i statystykach, ponieważ różne rozkłady prawdopodobieństwa, takie jak rozkład normalny, Poisson i inne, można wyrażać za pomocą funkcji wykładniczych.

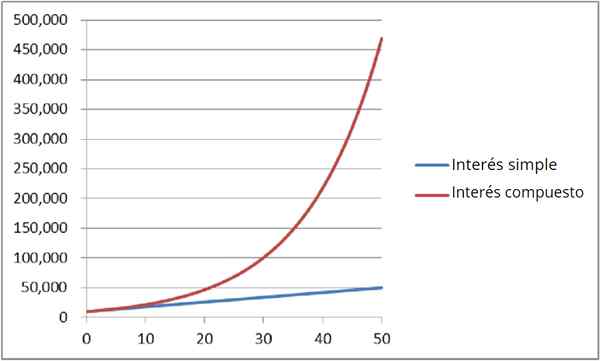
Ciągłe zainteresowanie złożone

Rysunek 4: Porównanie prostego i złożonego zainteresowania

Nazywa się to również Ciągła kapitalizacja. Poznać kwotę pieniędzy DO Masz później T lata, stosuje się ekspresję wykładniczą:

A (t) = p ⋅ e^Rt

Gdzie P jest pierwotnie zdeponowaną kwotą pieniędzy, R to stopa procentowa rocznie i wreszcie T to liczba lat.

Wzrost bakterii

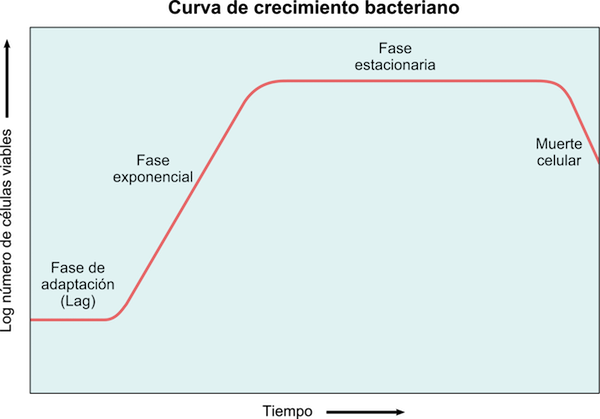Rycina 5: Krzywa wzrostu bakteryjnego, w której obserwuje się opóźnienie, wykładnicze, stacjonarne i śmierci

Bakterie rosną wykładniczo, więc wzrost może być modelowany przez:

N (t) = n_albo ⋅ e ^Kt

Gdzie n (t) jest istniejącą populacją za czasem t (prawie zawsze w godzinach), n_albo Jest to początkowa populacja, a K jest stała, która zależy od rodzaju bakterii i warunków, w których dostępne składniki odżywcze.

Rozkład radioaktywny

Niektóre jądra w naturze są niestabilne, więc odmawiają przekształcenia w bardziej stabilne, proces, który może być bardzo krótki lub potrwa tysiące lat, w zależności od izotopu. Podczas radioaktywnych cząstek rozpadu są emitowane, a czasem także fotony.

Niektóre radioaktywne izotopy mają zastosowania medyczne, na przykład radioaktywne jod I-131, które lekarze stosują w diagnozowaniu i leczeniu niektórych stanów tarczycy.

Rozkład radioaktywny jest modelowany przez funkcję wykładniczą.

Może ci służyć: ile dziesiątych jest w jednostce?

Rozwiązane ćwiczenia

Równania, w których nieznany pojawia się jako wykładnik, nazywane są równaniami wykładniczymi. Aby wyczyścić wartość nieznanego, stosuje się różne manipulacje algebraiczne i użycie funkcji logarytmu, która jest odwrotną funkcją wykładniczą.

Spójrzmy na rozwiązane ćwiczenia, które ilustrują punkt.

- Ćwiczenie 1

Rozwiąż następujące równania wykładnicze:

do 5^X = 625

b) 5^X = 2^X-1

Rozwiązanie

Liczba 625 jest wielokrotnością 5, w efekcie podczas jej rozkładu stwierdzamy, że:

625 = 5⁴

Dlatego możemy napisać:

5^X = 5⁴

Ponieważ podstawy są równe zarówno lewej, jak i prawej, możemy dopasować wykładniki i uzyskać:

x = 4

Rozwiązanie b

W tym ćwiczeniu nie możemy uciekać się do wcześniejszej techniki, ponieważ podstawy nie są takie same. Ale możemy zastosować logarytm po obu stronach równości, w ten sposób:

5^X = 2^X-1

Log (5^X) = log (2^X-1)

Teraz stosowana jest następująca właściwość logarytmów:

Log m^N = n⋅log m

I pozostaje:

x⋅log 5 = (x-1) ⋅log 2

x⋅ (log 5 - log 2) = -log 2

x = - log 2 ÷ (log 5 - log 2)

- Ćwiczenie 2

Wskaż, jaką funkcję odpowiada każdemu z pokazanych poniżej wykresów:

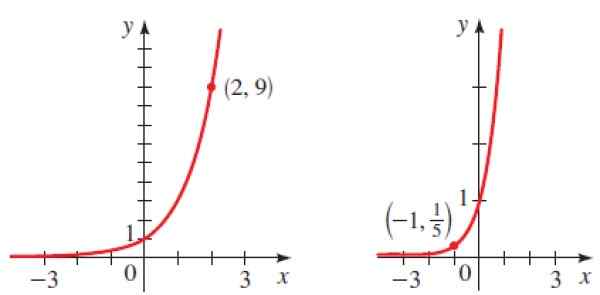Rysunek 6. Grafika Parast wykładniczych funkcji rozwiązanego ćwiczenia 2. Źródło: Stewart. J. Przedłużanie.

Rozwiązanie

Ponieważ jest to rosnący wykres, B jest większy niż 1 i wiemy, że punkt (2.9) należy do wykresu, dlatego:

y = b^X → 9 = B²

Wiemy, że 3² = 9, a zatem b = 3, a funkcja wynosi y = 3^X

Rozwiązanie b

Ponownie wymieniamy dany punkt (-1, 1/5) przy y = b^X Aby uzyskać:

1/5 = b^-1 = 1/b

Wówczas b = 5, a poszukiwana funkcja to:

y = 5^X

Bibliografia

1. Figuera, J. 2000. Matematyka 1st. Urozmaicony. Edycje CO-Bo.
2. Gid Hoffmann, J. Wybór problemów matematycznych na czwartym miejscu. Rok. Wyd. SPPHINX.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Larson, r. 2010. Obliczanie zmiennej. 9na. Wydanie. McGraw Hill.
5. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.