Rosnąca funkcja Jak to zidentyfikować, przykłady, ćwiczenia

Masz jeden Rosnąca funkcja Gdy wartość y wzrasta, jeśli X również wzrasta, w przeciwieństwie do zmniejszających się funkcji, w których wartość i zmniejsza się, gdy X wzrasta.

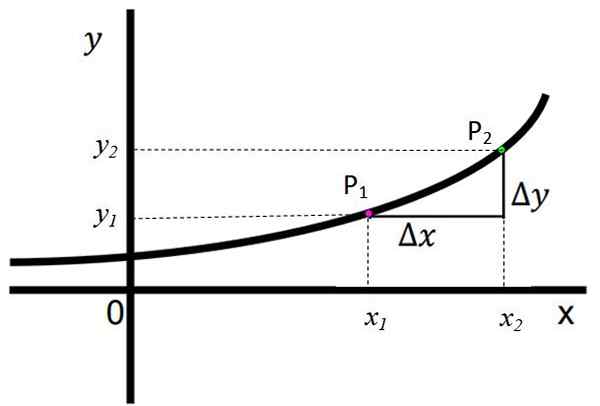
Poniższy rysunek pokazuje funkcję rosnącą i wyraźnie obserwuje się, że podczas przechodzenia od lewej do prawej na osi x, wartość odpowiedniej współrzędnej i, równoważna F (x), stopniowo rośnie. Mówi się, że jeśli wszystko x₂ > x₁, Wtedy istnieje i₂ > i₁.

Rysunek 1. Rosnąca funkcja. Źródło: f. Zapata.

Punkty str₁ I p₂ Są pokazywane odpowiednio współrzędne (x₁, I₁) i (x₂,I₂). Są zdefiniowane:

Δy = y₂ -I₁

Δx = x₂ -X₁

W tej funkcji zarówno δy, jak i Δx mają znak dodatni, co oznacza, że ​​i₂ > i₁ i x₂ > x₁, odpowiednio. Jest to wyraźny znak, że funkcja skutecznie rośnie.

Dobrym przykładem zawsze rosnącej funkcji (rosnącego monotonnego) jest neperiański logarytm liczby rzeczywistej. Im wyższa liczba, tym większy logarytm.

[TOC]

Jak zidentyfikować rosnącą funkcję?

W prostej i ciągłej funkcji, jak pokazano na rysunku 1, łatwo jest ustalić, czy funkcja rośnie lub maleje, pod warunkiem, że wykres jest dostępny.

Jednak bardziej złożone funkcje mogą rosnąć w niektórych odstępach czasu i zmniejszać się w innych. Dlatego rozmawiamy Odstępy wzrostu i zmniejszyć funkcji.

W sieci znajdują się bezpłatna grafika online, taka jak Geogebra, które pozwalają na grafiki wszelkiego rodzaju funkcji. Mając wykres, łatwo jest ustalić, czy funkcja zawsze rośnie, taka jak f (x) = log x lub czy ma odstępy, w których rośnie, i inne, w których maleje i co to jest.

Kryterium pierwszej pochodnej

Biorąc pod uwagę pewien przedział liczbowy I, jeśli iloraz między wielkościami δy i δx jest dodatni, funkcja rośnie. I wręcz przeciwnie, jeśli jest ujemna, funkcja maleje.

Może ci służyć: prawdopodobieństwo częstotliwości: koncepcja, jak jest obliczane i przykłady

Musisz:

ΔY / Δx> 0 → Funkcja uprawy

Fakt, że δY / Δx> 0 i funkcja rośnie w pewnym odstępie, sugeruje, że pierwsze pochodzenie z funkcji, a raczej jej znaku, może być wykorzystane jako kryterium w celu ustalenia, czy w efekcie funkcja rośnie w określonym odstęp lub nawet w pewnym momencie twojej domeny.

Rzeczywiście, pierwsza pochodna jest definiowana jako nachylenie krzywej w każdym punkcie:

Co oznacza, że ​​δx można wykonać tak małe, jak chcesz. Jeśli f '(x)> 0 dla określonej wartości x, na przykład x = a, nachylenie krzywej w tym punkcie f' (a) jest dodatnie, a funkcja będzie się tam zwiększać.

Poniższe twierdzenie oferuje kryterium, aby wiedzieć, kiedy funkcja rośnie w przedziale (a, b):

Twierdzenie

Niech f (x) będzie funkcją pochodną w (a, b). Jeśli f '(x)> 0, dla dowolnej wartości x należących do wspomnianego odstępu, mówi się, że f (x) rośnie w (a, b).

Twierdzenie jest stosowane, aby dowiedzieć się, w których odstępie rosną funkcję, zgodnie z tymi krokami:

Krok 1

Znajdź punkty, w których f '(x) = 0, a także te, w których F' (x) nie istnieje. Te, nazywane punkt krytyczny, Są to punkty, w których f '(x) może zmienić znak, a zatem f (x) ma możliwość przejścia od wzrostu do zmniejszenia lub odwrotnie.

Krok 2

Znajdź znak F '(x) dla wartości dowolnej w każdym z przedziałów określonych przez punkty znalezione w kroku 1.

Krok 3

Użyj twierdzenia, aby wiedzieć, czy funkcja rośnie, czy nie w każdym przedziale.

Przykłady rosnących funkcji

Istnieją funkcje, które mają pewne odstępy wzrostu i inne spadki, ale te pokazane poniżej rosną.

Waga oparta na wieku

Waga osoby od czasu jej narodzin, aż do około zakończenia okresu dojrzewania, jest prawie zawsze rosnącą funkcją wieku. Niemowlęta i dzieci rosną i rozwijają się na przestrzeni lat, a następnie, gdy osiągną dorosłość, reszta ich życia ma utrzymać stabilną wagę, chociaż wzloty i upadki są bardzo częste.

Może ci służyć: linia pionowa

Funkcja logarytmu

Funkcje realnego logarytmu Neperian f (x) = ln x i logarytm dziesiętny f (x) = log x zawsze rosną.

Funkcja pierwiastka kwadratowego liczby rzeczywistej

Inną funkcją, która zawsze rośnie, jest funkcja pierwiastka kwadratowego pozytywnej liczby rzeczywistej:

y = √x

Powiązana funkcja i funkcja liniowa

Powiązana funkcja:

f (x) = MX + B

Rośnie, gdy linia jest dodatnim nachyleniem. Podobnie funkcje tożsamości i liniowej:

f (x) = x i f (x) = ax, z a> 0

Rosną w całej swojej domenie.

Funkcja wykładnicza

Funkcja wykładnicza, taka jak f (x) = e^X  I ogólnie funkcja formy:

f (x) = a^X, Z> 1

Rosną w całej swojej domenie.

Potencjalna funkcja indeksu impar

Potencjalne funkcje dziwnego wykładnika, takie jak te:

• f (x) = x³
• g (x) = x⁵

Zawsze rosną.

Ćwiczenia

Ćwiczenie 1

Określ, w których odstępach funkcji reprezentowanej na poniższym wykresie rośnie:

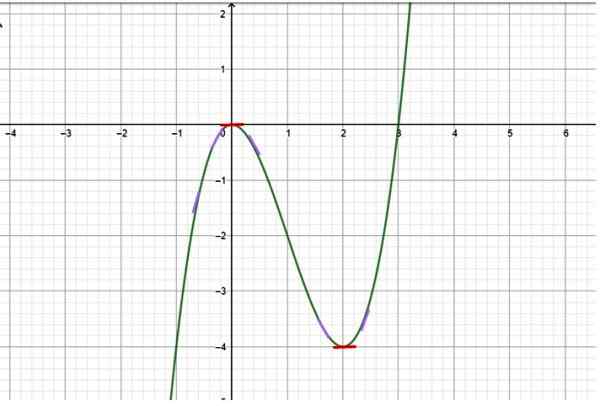Rysunek 2. Funkcja z interwałami wzrostu i zmniejszania. Źródło: f. Zapata.

Rozwiązanie

Ponieważ wykres jest dostępny, na podstawie uważnej obserwacji ustalono, że funkcja ma następujące zachowanie:

-Od x → -∞ do x = 0 funkcja rośnie, ponieważ wartości y stają się coraz mniej ujemne. Purple narysowano małe segmenty nachylenia, aby wskazać nachylenie linii stycznej do krzywej w różnych punktach (nachylenie stycznej do krzywej jest dokładnie jego pierwszą pochodną).

Segmenty te mają dodatnie nachylenie, więc twierdzenie zapewnia, że ​​funkcja rośnie w tym przedziale.

-Ale przy x = 0 nachylenie krzywej jest anulowane, co jest wskazane małym poziomym czerwonym segmentem. To jest punkt krytyczny funkcji.

Może ci służyć: po co matematyka i po co są? 7 ważnych aplikacji

Stamtąd funkcja zaczyna się zmniejszać, stając się bardziej negatywnymi wartościami i. Ta sytuacja trwa do x = 2, co jest kolejnym punktem krytycznym.

Następnie w przedziale od x = 0 do x = 2 funkcja maleje.

-Od x = 2 funkcja staje się coraz mniej ujemna, aż do x = 3 przekroczy oś x i nadal staje się bardziej dodatnia. Dlatego jest to przedział wzrostu.

Wniosek: Odstępy wzrostu wynoszą (-∞, 0) i (2, ∞+), podczas gdy przedział zmniejszania wynosi (0,2).

Ćwiczenie 2

Określ przedziały wzrostu następującej funkcji, poprzez kryteria pierwszej pochodnej:

f (x) = x² - 2x

Rozwiązanie

Zgodnie z powyższymi krokami pierwsza pochodna jest obliczana i równa się 0, aby znaleźć punkty krytyczne:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Ta wartość określa istnienie przedziałów (-∞, 1) i (1, ∞+). Wybrano dwie dowolne wartości, które należą do każdego:

-Dla x = 0, który należy do (-∞, 1), musisz F '(0) = 2.0 - 2 = -2. Ponieważ wynik jest ujemny, funkcja maleje w tym przedziale.

-Dla x = 3, należący do (1, ∞+), pierwsza pochodna jest warta f '(3) = 2.3 - 2 = 4. Ponieważ wynik jest pozytywny, stwierdza się, że funkcja rośnie w tym przedziale.

Czytnik może wykres oryginalnej funkcji f (x) = x² - 2x na grafice online, aby potwierdzić ten wynik.

Bibliografia

1. Ayres, f. 2000. Obliczenie. 5Ed. MC Graw Hill.
2. Leithold, L. 1992. Obliczanie za pomocą geometrii analitycznej. Harla, s.DO.
3. Purcell, e. J., Varberg, d., & Rigdon, s. I. (2007). Obliczenie. Meksyk: Pearson Education.
4. Matemobile. Funkcje, rosnące, malejące i stałe. Odzyskany z: Matemovil.com
5. Requena, ur. Rosnące funkcje. Odzyskane z: Universoformulas.com.
6. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.