Funkcja stałej cechy, przykłady, ćwiczenia

stała funkcja Jest to, w którym wartość i. Innymi słowy: stała funkcja zawsze ma formę  f (x) = k, Gdzie k To jest liczba rzeczywista.

Poprzez wykres stałej funkcji w układzie współrzędnych Xy, Zawsze jest to linia prosta równoległa do osi poziomej lub osi X.

Rysunek 1. Wykres kilku stałych funkcji na płaszczyźnie kartezjańskim. Źródło: Wikimedia Commons. Użytkownik: Hite [domena publiczna]

Ta funkcja jest szczególnym przypadkiem Powiązana funkcja, którego wykres jest również linią prostą, ale z nachyleniem. Stała funkcja ma zerowe w toku, to znaczy jest linią poziomą, jak pokazano na rycinie 1.

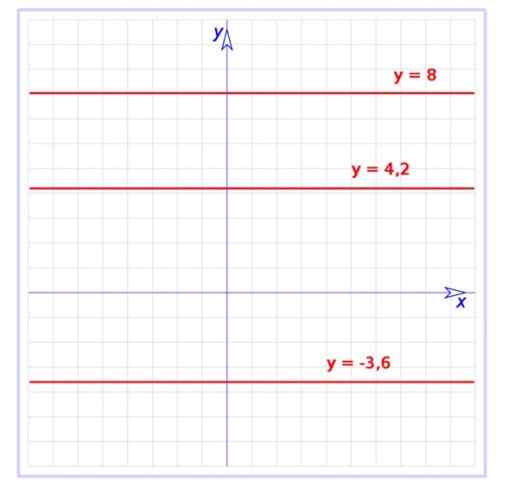
Istnieje wykres trzech stałych funkcji:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Wszystkie są proste równolegle do osi poziomej, pierwsza jest poniżej tej osi, podczas gdy pozostałe są powyżej.

[TOC]

Charakterystyka stałej funkcji

Możemy podsumować główne cechy stałej funkcji w następujący sposób:

-Jego wykres jest poziomą linią prostą.

-Ma unikalne skrzyżowanie z osą I, wartość k.

-Jest ciągły.

-Opanowanie funkcji stałej (zestaw wartości, które są X) to zestaw liczb rzeczywistych R.

-Trasa, zakres lub sprzeczność (zestaw wartości, które zmienna przyjmuje I) to po prostu stała k.

Przykłady

Funkcje są niezbędne do ustalenia powiązań między wielkościami, które w pewnym sensie zależą od siebie. Istniejąca relacja między nimi można modelować matematycznie, aby wiedzieć, jak jedno z nich zachowuje.

Może ci służyć: papomudas

Pomaga to budować modele w wielu sytuacjach i przewidywać ich zachowanie i ewolucję.

Pomimo pozornej prostoty, stała funkcja ma wiele zastosowań. Na przykład, jeśli chodzi o studiowanie wielkości, które pozostają stałe w czasie, a przynajmniej przez znaczny czas.

W ten sposób wielkości zachowują się w sytuacjach takich jak następujące:

- prędkość Rejs po samochodzie, który porusza się po długiej prostoliniowej autostradzie. Tak długo, jak nie zatrzymuje się ani nie przyspiesza, samochód przenosi jednolity ruch prostoliniowy.

Rysunek 2. Jeśli samochód nie zatrzymuje się ani nie przyspiesza, ma jednolity ruch prostoliniowy. Źródło: Pixabay.

-W pełni załadowany i odłączony kondensator od obwodu, ma ciężar stały w czasie.

-Wreszcie parking z płaską stawką, utrzymuje cena stały bez względu na to, jak długo tam zaparkował samochód.

Inny sposób reprezentowania stałej funkcji

Stała funkcja na przemian może być reprezentowana w następujący sposób:

f (x) = kx⁰

Ponieważ każda wartość X W rezultacie podniesiony do 0 daje 1, poprzednie wyrażenie jest zredukowane do znajomych:

f (x) = k

Oczywiście dzieje się to tak długo, jak wartość k różni się od 0.

Dlatego stała funkcja jest również klasyfikowana jako funkcja wielomianu klasa 0, ponieważ wykładnik zmiennej X To jest 0.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Odpowiedz na następujące pytania:

a) Czy można potwierdzić, że linia podana przez x = 4 jest funkcją stałą? Powód twojej odpowiedzi.

b) Czy stała funkcja może mieć skrzyżowanie z osą x?

c) to funkcja f (x) = w stała²?

Odpowiedz

Oto wykres linii x = 4:

Może ci służyć: zmienne statystyczne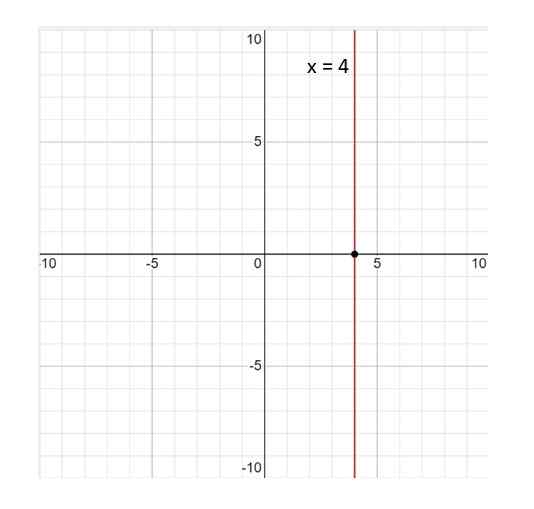 Rysunek 3. Wykres linii x = 4. Źródło: f. Zapata.

Linia x = 4 nie jest funkcją; Z definicji funkcja jest taka, że ​​z każdą wartością zmiennej X Odpowiada jednej wartości I. I w tym przypadku nie jest to spełnione, ponieważ wartość x = 4 jest związany z nieskończonymi wartościami I. Dlatego odpowiedź brzmi nie.

Odpowiedź b

Zasadniczo stała funkcja nie ma przecięcia z osą X, Chyba że tak jest y = 0, w takim przypadku jest to oś X Właściwie powiedział.

Odpowiedź c

Tak, od czasu W Jest stały, jego kwadrat jest również. Cóż to za zainteresowanie W Nie zależy od zmiennej wejściowej X.

- Ćwiczenie 2

Znajdź skrzyżowanie między funkcjami f (x) = 5 I G (x) = 5x - 2

Rozwiązanie

Aby znaleźć przecięcie tych dwóch funkcji, można je odpowiednio przepisać jako:

y = 5; y = 5x - 2

Są dopasowane, uzyskując:

5x - 2 = 5

Które jest równaniem liniowym pierwszego stopnia, którego rozwiązaniem jest:

5x = 5+2 = 7

x = 7/5

Punkt przecięcia to (7/5; 5).

- Ćwiczenie 3

Wykazać, że ten pochodzący ze stałej funkcji wynosi 0.

Rozwiązanie

Z definicji pochodnej masz:

 f (x) = k

f (x+h) = k

Zastąpienie definicji:

Powyższe ma sens, ponieważ pochodna funkcji jest zdefiniowana jako nachylenie stycznej linii do krzywej w danym punkcie. Stała funkcja ma zerową w toku i każdą linię styczną.

Ponadto, jeśli myślimy o pochodnej jako kursie walut DY/DX, Stała funkcja nie doświadcza żadnej zmiany, dlatego jej pochodna jest nieważna.

Może ci służyć: Zasada multiplikatywna: Techniki zliczania i przykłady

- Ćwiczenie 4

Znajdź nieokreśloną całkę f (x) = k.

Rozwiązanie

- Ćwiczenie 5

Firma telefoniczna komórkowa oferuje nieograniczoną liczbę usług internetowych z płaską stawką płacącą 15 USD miesięcznie. Jaka jest funkcja cenowa według czasu?

Rozwiązanie

Niech P będzie ceną, którą należy zapłacić w czasie $ i t, co można wyrazić w ciągu kilku dni. Funkcja jest ustalana w następujący sposób:

P (t) = 15

- Ćwiczenie 6

Poniższy wykres w porównaniu z czasem odpowiada ruchowi cząstki.

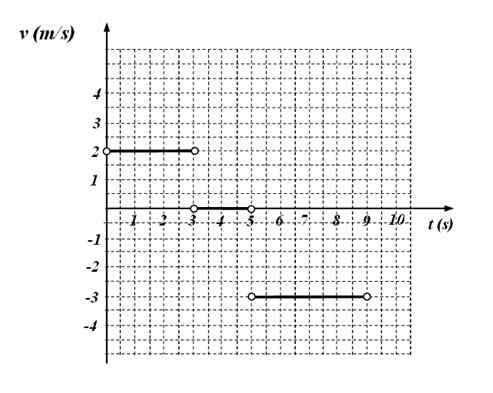Rysunek 4. Funkcja V (t) Wykres funkcji dla ćwiczenia 6. Źródło: f. Zapata.

Jest to żądane:

a) Napisz wyrażenie dla funkcji prędkości jako funkcja czasu V (t).

b) Znajdź odległość przebywającą przez telefon komórkowy w przedziale czasowym od 0 do 9 sekund.

Rozwiązanie

Wykresu pokazującego:

-V = 2 m/s W przedziale czasowym od 0 do 3 sekund

-Telefon komórkowy jest zatrzymany między 3 a 5 sekundami, ponieważ w tym przedziale prędkość jest warta 0.

-V = - 3 m/s Od 5 do 9 sekund.

Jest przykładem kawałków lub funkcji w częściach, które z kolei składają się z stałych funkcji, ważnych tylko dla wskazanych przedziałów czasowych. Stwierdzono, że poszukiwana funkcja to:

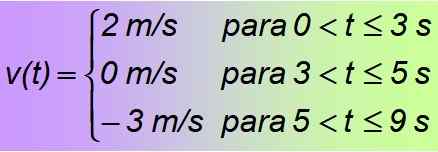
Rozwiązanie b

Z wykresu V (t) można obliczyć odległość przebywającą przez telefon. Tą drogą:

-Odległość przebywana między 0 a 3 sekundą = 2 m/s . 3 s = 6 m

-Od 3 do 5 sekund został zatrzymany, dlatego nie przejechał odległości.

-Odległość przebywana między 5 a 9 sekundami = 3 m/s . 4 s = 12 m

W sumie telefon komórkowy koncertował 18 m. Zobacz, że chociaż prędkość jest ujemna w przedziale między 5 a 9 sekundami, przebyta odległość jest dodatnia. To, co się dzieje, polega na tym, że w tym czasie telefon komórkowy zmienił znaczenie swojej prędkości.

Bibliografia

1. Geogebra. Stałe funkcje. Odzyskany z: Geogebra.org.
2. Maplesoft. Stała funkcja. Odzyskane z: Maplesoft.com.
3. Wikilibros. Obliczanie w funkcji zmiennej/funkcji/stałej. Odzyskane z: jest.Wikibooks.org.
4. Wikipedia. Stała funkcja. Źródło: w:.Wikipedia.org
5. Wikipedia. Stała funkcja. Odzyskane z: jest.Wikipedia.org.