Matematyka

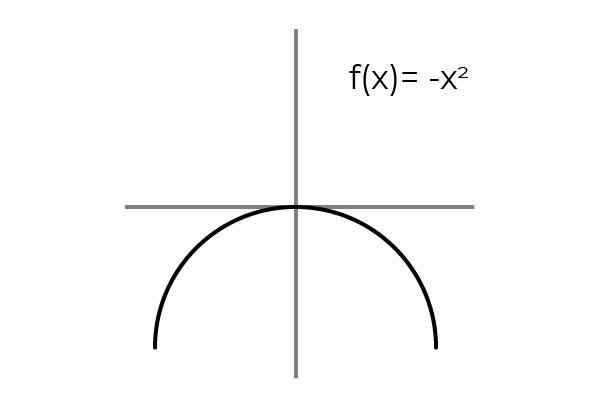
Funkcja bijekcyjna Czym jest, jak to się dzieje, przykłady, ćwiczenia

Funkcja bijekcyjna Czym jest, jak to się dzieje, przykłady, ćwiczenia

A Funkcja biejcive Jest to taki, który spełnia podwójny stan bycia Wstrzykiwanie i zatwierdzenie. Oznacza to, że wszystkie elementy domeny mają pojedynczy obraz w Codominium, a z kolei Codominium jest równe zakresowi funkcji ( RF ).

Jest to spełnione, gdy rozważana jest biuniwokalna zależność między elementami domeny i kodominium. Prostym przykładem jest funkcja F: r → R zdefiniowane przez linię F (x) = x

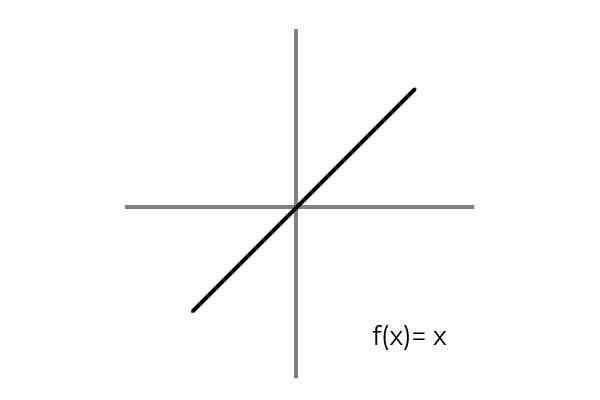Źródło: Autor

Zaobserwowano, że dla każdej wartości domeny lub zestawu odlotu (oba warunki obowiązują jednakowo), w zestawie Codominium lub zestaw. Ponadto nie ma elementu Codominium, który nie jest obrazem.

Zatem F: r → R zdefiniowane przez linię F (x) = x jest bijektyw

[TOC]

Jaka jest funkcja bijkłowców?

Aby odpowiedzieć na to, konieczne jest posiadanie jasnych pojęć związanych z Wtryskiwanie I Otmigowanie funkcji, Oprócz kryteriów funkcji warunkowania w celu dostosowania ich do wymagań.

Wtryskiwanie funkcji

Funkcja jest Invicitive Gdy każdy z elementów jej domeny jest związany z pojedynczym elementem Codominium. Element Codominium może być tylko obrazem pojedynczego elementu domeny, w ten sposób nie można powtórzyć wartości zmiennej zależnej.

Rozważyć Invicitive Następujące należy spełnić funkcję:

∀ x1  ≠ x2   ⇒ F (x1 ) ≠ f (x2 )

Otmigowanie funkcji

Funkcja jest klasyfikowana jako Zadowocka, Jeśli każdy element jego kodominium jest obrazem co najmniej jednego elementu domeny.

Rozważyć Zadowocka Następujące należy spełnić funkcję:

Może ci służyć: próbkowanie zastępcze

Być F: dF → CF

∀ B ℮ CF  I do ℮  DF   / F (a) = b

To jest algebraiczny sposób ustalenia, że ​​dla każdego „b” należy do cF Istnieje „A”, który należy do DF tak, że funkcja oceniana w „A” jest równa „B”. 

Warunkowanie funkcji

Czasami funkcja, która nie jest Bijecveive, może przejść pewne warunkowanie. Te nowe warunki mogą zamienić go w Funkcja biejcive. Wszystkie rodzaje modyfikacji domeny i kodominium funkcji są prawidłowe, w których celem jest spełnienie właściwości iniekcji i nadmiernie -allchecyjności w odpowiedniej relacji.

Przykłady: Rozwiązane ćwiczenia

Ćwiczenie 1

Być funkcją F: r → R zdefiniowane przez linię F (x) = 5x +1

Odp.: [Wszystkie liczby rzeczywiste]

Obserwuje się, że dla dowolnej wartości domeny jest obraz w kodominium. Ten obraz jest wyjątkowy, co czyni F być jednością Funkcja iniekcyjna. W ten sam sposób obserwujemy, że kodominium funkcji jest równe jej zakresowi. W ten sposób spełnianie stanu Otrukowanie.

Bycie iniekcyjnym i zatwierdzającym jednocześnie możemy to stwierdzić

F: r → R zdefiniowane przez linię F (x) = 5x +1 jest Funkcja biejcive.

Dotyczy to wszystkich funkcji liniowych (funkcji, których większy stopień zmiennej to jeden).

Ćwiczenie 2

Być funkcją F: r → R określony przez F (x) = 3x2 - 2

Podczas rysowania poziomej linii obserwuje się, że wykres znajduje się więcej niż jeden raz. Z tego powodu funkcja F Nie jest inicjatywne i dlatego nie będzie Bijecveive Podczas gdy jest zdefiniowany R → R

W ten sam sposób istnieją wartości kodominium, które nie są obrazami żadnego elementu domeny. Z tego powodu funkcja nie jest zatrzymująca, co również zasługuje na kondycjonowanie zestawu przyjazdu.

Może ci służyć: SET Teoria: Charakterystyka, elementy, przykłady, ćwiczenia

Domena i kodominium funkcji są uwarunkowane

                                               F: [0 , ∞] → [ - 2 , ∞ ]

Gdzie obserwuje się, że nowa domena obejmuje wartości od zera do dodatniej nieskończoności. Unikanie powtarzania wartości, które wpływają na wstrzykiwanie.

Zatem kodominium zostało zmodyfikowane, licząc od „-2” do dodatniej nieskończoności, eliminując z kodominium wartości, które nie odpowiadały żadnemu elementowi domeny

W ten sposób można to zapewnić F : [0 , ∞] → [ - 2 , ∞ ] określony przez F (x) = 3x2 - 2

Jest bijective

Ćwiczenie 3

Być funkcją F: r → r określony przez F (x) = sin (x)

W przedziale [[[ -∞ , +∞ ] Funkcja zatok zmienia wyniki między zero a jednym.

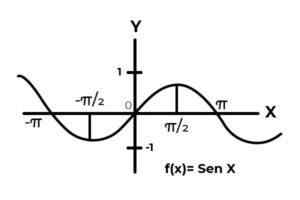Źródło: Autor.

Funkcja F Nie odpowiada kryteriom iniekcyjności i przepisywności, ponieważ wartości zmiennej zależnej są powtarzane w każdym przedziale π. Oprócz warunków Codominium poza przedziałem [-eleven] Nie są obrazem żadnego elementu domeny.

Podczas studiowania grafiki funkcji F (x) = sin (x) przedziały obserwuje się, gdzie zachowanie krzywej spełnia kryteria Bijectność. Takie jak interwał  DF  = [[[  π/2,3π/2  ] Dla domeny. I CF  = [-1, 1] Dla Codominium.

Gdzie funkcja zmienia się wyniki od 1 do -1, bez powtarzania żadnej wartości w zmiennej zależnej. A jednocześnie Co -oooRium jest równe wartościom przyjętym przez wyrażenie Sin (x)

W ten sposób funkcja F: [  π/2,3π/2  ] → [-1, 1]  określony przez F (x) = sin (x). Jest bijective

Ćwiczenie 4

Podnieś niezbędne warunki dla DF i CF. Tak wyrażenie

Może ci służyć: Błąd próbkowania: wzory i równania, obliczenia, przykłady

F (x) = -x2  Być bitwarką.

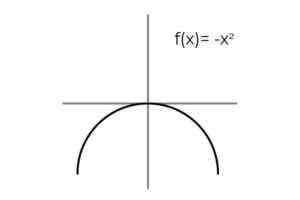Źródło: Autor

Powtarzanie wyników obserwuje się, gdy zmienna przyjmuje przeciwne wartości:

F (2) = f (-2) = -4

F (3) = f (-3) = -9

F (4) = f (-4) = -16

Domena jest uwarunkowana, ograniczając ją do prawej strony prawdziwej linii.

DF = [0 , +∞ ]

W ten sam sposób obserwuje się, że zakres tej funkcji jest przedział [[[ -∞ , 0], co, służąc jako Codominium, spełnia warunki zatwierkania.

W ten sposób możemy to zakończyć

Ekspresja F: [0 , +∞ ] → [ -∞ , 0] określony przez F (x) = -x2   Jest bijective

Proponowane ćwiczenia

Sprawdź, czy następujące funkcje są biustonose:

F: [0 , ∞) → R określony przez F (x) = 3 (x + 1)2  +2

F: [ 3π/2,5π/2  ] → R określony przez F (x) = 5ctg (x)

F: [ -π,π  ] → R określony przez F (x) = cos (x - 3)

F: r → R zdefiniowane przez linię F (x) = -5x + 4

Bibliografia

  1. Wprowadzenie do logiki i krytycznego myślenia. Merrilee H. Łosoś. University of Pittsburgh
  2. Problemy w analizie matematycznej. Piotr Bilar, Alfred Witkowski. University of Wroclaw. Polak.
  3. Elementy analizy abstrakcyjnej. Mícheál O'Searcoid Phd. Departament Matematyki. University College Dublin, Beldfield, Dubllind 4
  4. Wprowadzenie do logiki i metodologii nauki dedukcyjnej. Alfred Tarski, Nowy Jork Oxford. Oxford University Press.
  5. Zasady analizy matematycznej. Enrique Linés Escardó. Redakcja Reverté s. Do 1991. Barcelona, ​​Hiszpania.