Siły ścinające siły powierzchniowe i masowe

Wysłuchaj siły Jest to siła złożona, która charakteryzuje się wywieraniem równoległym do powierzchni i ma tendencję do dzielenia ciała, wypierając ze sobą sekcje wynikające z cięcia.

Schematycznie jest reprezentowany na rycinie 1, który pokazuje siłę ścinającą przyłożoną na dwa różne punkty drewnianego ołówka. Z kolei siła ścinania wymaga dwóch równoległych i przeciwnych sił, które w zależności od ich intensywności są zdolne do odkształcenia ołówka lub zdecydowanie pęknięcie.

Rysunek 1. Przyłożona siła ścinająca z rękami powoduje rozkład ołówka. Źródło: Pixabay.

Tak więc, nawet jeśli mówisz o pojedynczej sile Hear, faktycznie mają zastosowanie dwa siły, ponieważ siła ścinająca to siła złożona. Siły te składają się z dwóch sił (lub więcej, w złożonych przypadkach) zastosowane w różnych punktach obiektu.

Dwie siły o tej samej wielkości i przeciwny kierunek, ale z równoległymi liniami działania, stanowią a para sił. Pary nie zapewniają tłumaczenia na obiekty, ponieważ ich wynik jest nieważny, ale zapewniają moment obrotowy netto.

Z parą obiekty takie jak kierownica pojazdu są obracane lub mogą się deformować i pękać, jak w przypadku ołówka i stolika drewna pokazanego na rycinie 2.

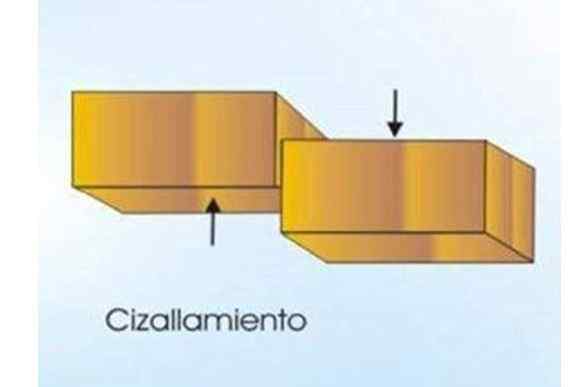Rysunek 2. Siła ścinająca dzieli drewniany bar na dwie sekcje. Zauważ, że siły są styczne do przekroju Madero. Źródło: f. Zapata.

[TOC]

Siły powierzchniowe i siły masowe

Siły złożone są częścią połączeń siły powierzchniowe, Właśnie dlatego, że stosują się na powierzchni ciał i nie są w żaden sposób powiązane z ich masą. Aby wyjaśnić ten punkt, porównajmy te dwie siły, które często działają na obiektach: waga i siła tarcia.

Może ci służyć: Graff Van Generator: Partie, jak to działa, aplikacje

Wielkość masy wynosi p = mg i ponieważ zależy od ciała ciała, nie jest to siła powierzchniowa. To jest Siła masowa, A waga jest najbardziej charakterystycznym przykładem.

Jednak tarcie zależy od charakteru powierzchni kontaktowych, a nie od masy ciała, na której działa, jest to dobry przykład powierzchownych sił częstego wyglądu.

Proste siły i siły złożone

Siły powierzchowne mogą być prosty albo Związki. Widzieliśmy już przykład siły złożonej w sile ścinającej, a z drugiej strony tarcie jest reprezentowane jako prosta siła, ponieważ pojedyncza strzałka wystarczy, aby przedstawić ją na schemacie ciała izolowanym z obiektu.

Proste siły są odpowiedzialne za drukowanie zmian w ruchu ciała, na przykład wiemy, że siła tarcia kinetycznego między ruchomym obiektem a powierzchnią, na której się porusza, powoduje zmniejszenie prędkości.

Przeciwnie, siły kompozytowe mają tendencję do odkształcenia ciał, aw przypadku ścinania lub ścinania końcowym wynikiem może być cięcie. Inne siły powierzchniowe, takie jak napięcie lub kompresja, wydłużają lub ściskają ciało, na którym działają.

Za każdym razem, gdy pomidor jest cięty w celu przygotowania sosu lub nożyczek do sekcji arkuszu papieru, stosowane są opisane zasady. Narzędzia tnące zwykle mają dwie ostre arkusze metali do nałożenia siły ścinania na przekroju obiektu do posiekanego.

Może ci służyć: jaki jest moment magnetyczny? Rysunek 3. Siła ścinająca w akcji: jedna z sił jest stosowana przez liść noża. Źródło: Zdjęcie jedzenia stworzone przez Katemangostar - Freepik.Jest

Usłyszeć stres

Wpływ siły ścinającej zależy od wielkości siły i obszaru, na którym działa, więc inżynieria koncepcji Usłyszeć stres, który uwzględnia zarówno siłę, jak i obszar.

Ten wysiłek ma inne znaczenia, takie jak Siła ścinania o Wysiłki cywilne i w konstrukcjach cywilnych jest to niezwykle ważne.

Jego użyteczność jest natychmiast rozumiana, gdy rozważa następującą sytuację: Załóżmy, że istnieją dwa pręty tego samego materiału, ale inna grubość, która jest narażona na rosnące siły, dopóki je złamią.

Oczywiste jest, że aby złamać najgrubszy pasek, musisz zastosować większą siłę, jednak wysiłek jest taki sam dla każdego paska, który ma ten sam skład. Takie eseje są częste w inżynierii, biorąc pod uwagę znaczenie wyboru odpowiedniego materiału dla prognozowanej struktury optymalnie działają.

Wysiłek i deformacja

Matematycznie, jeśli oznaczysz wysiłek ścinania jako τ, Do wielkości siły przyłożonej jako F i obszaru, na którym działa ona jako A, masz średni wysiłek ścinania:

τ_przeciętny= F /a

Będąc ilorazem między siłą a obszarem, jedność wysiłków w systemie międzynarodowym jest Newton/M², Nazywany Pascal i skrócony jako PA. W systemie angielskim używane jest funt/stopa ² i funta /cal².

Może ci służyć: Rozwiązanie ciepło: jak jest obliczane, zastosowania i ćwiczenia

Jednak w wielu przypadkach obiektem pod wpływem ścinania są odkształcenia, a następnie odzyskuje swoją pierwotną formę bez łamania, gdy wysiłek przestanie działać. Załóżmy, że deformacja składa się z zmiany długości.

W takim przypadku wysiłek i deformacja są proporcjonalne, dlatego można podnieść następujące:

Siła ścinania ∝ Jednostkowe deformacje

Symbol ∝ Oznacza „proporcjonalne do”, a jeśli chodzi o jednolite odkształcenie, jest on definiowany jako stosunek między zmianą długości, który zostanie nazywany ΔL a pierwotną długością, zwaną L_albo. Tą drogą:

τ ∝ (ΔLl_albo)

Moduł ścinania

Będąc stosunkiem między dwiema długościami, jednolite odkształcenie nie ma jednostek, ale przy umieszczaniu równego symbolu stała proporcjonalności musi je zapewnić. Wołanie G, aby powiedzieć Constant:

τ = G (δLl_albo)

G jest nazywane Usłyszeć moduł o Moduł cięty. Ma jednostki pasji w systemie międzynarodowym, a jego wartość zależy od charakteru materiału. Możliwe jest określenie takich wartości w laboratorium, przećwiczenie działania różnych sił na różnorodne próbki składu.

Gdy konieczne jest określenie wielkości siły ścinającej z poprzedniego równania, wystarczy zastąpić definicję wysiłku:

τ = F /a = g (δLl_albo)

I jasne:

F = a × g (δLl_albo)

Siły tnące są bardzo częste, a ich skutki należy wziąć pod uwagę w wielu aspektach nauki i technologii. W konstrukcjach pojawiają się w punktach wsparcia wiązek, mogą powstać podczas wypadku i złamać kości, a jej obecność jest w stanie zmienić działanie maszyny.

Działają na dużą skalę skorupy Ziemi, powodując złamania w skałach geologicznych i wypadkach, dzięki aktywności tektonicznej. Dlatego są również odpowiedzialne za ciągłe modelowanie planety.

Bibliografia

1. Piwo, f. 2010. Mechanika materiałów. 5. Wydanie. McGraw Hill. 7 - 9.
2. Fitzgerald, 1996. Mechanika materiałów. Alpha Omega. 21-23.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6^Tth  Wyd. Prentice Hall. 238-242.
4. Hibbeler, R.C. 2006. Mechanika materiałów. 6th. Wydanie. Edukacja Pearsona. 22 -25
5. Valera Negrete, J. 2005. Ogólne uwagi fizyki. Unam. 87-98.
6. Wikipedia. Stres ścinania. Odzyskane z: w.Wikipedia.org.