Matematyka

Frakcje równoważne 3/4

2184
232
Arkady Sawicki

Frakcje równoważne 3/4 Są tymi, w których dzieląc licznik między mianownik, powoduje to liczbę dziesiętną 0.75.

To zawsze jest możliwe. Jeśli wynik tej operacji jest równy 0.75, ułamek jest równoważny 3/4, na przykład ułamek 6/8:

Frakcja 6/8 jest równoważna ¾, ponieważ poprzez podzielenie licznika między mianownikiem, w obu przypadkach uzyskuje się 0.75. Źródło: f. Zapata.

Teraz ułamek 6/8 uzyskano przez pomnożenie zarówno licznika, jak i ¾ mianownika. Poprzez jednoczesne pomnożenie licznika i mianownika przez tę samą kwotę, wartość dziesiętna danej frakcji nie jest zmieniona, ale pozwala uzyskać ułamki równoważne danym.

Innym sposobem na znalezienie ułamka równoważnego innym byłoby podział licznika i mianownika przez tę samą kwotę. Jednak w przypadku ¾ nie można znaleźć takiej liczby, która dzieli się w tym samym czasie do 3 i 4, a wynik jest liczbą całkowitą. Wynika to z faktu, że 3 i 4 są ze sobą kuzynami, więc nie mają wspólnych dzielników.

Kiedy licznik i mianownik ułamka są ze sobą liczbami pierwszymi, mówi się, że ułamek jest nieskracalny. Dlatego ¾ jest nieredukowalny.

Sposoby na znalezienie ułamka równoważnego innym

Istnieją dwa bardzo proste sposoby znalezienia frakcji równoważnej innej danej frakcji: pierwsza jest redukcja, a druga przez wzmocnienie.

Redukcja i wzmocnienie ułamków

Zmniejszenie

Ta procedura polega na znalezieniu liczby, która jest dzielą zarówno licznika, jak i mianownika. Po znalezieniu zarówno licznikowy, jak i mianownik są podzielone przez tę wartość i natychmiast uzyskały ułamek równoważny oryginałowi. Weryfikuje się, że w ten sposób wykonuje stosunek licznika między mianownikiem a porównywaniem.

Może ci służyć: funkcje matematyczne

Kiedy nieredukowalna część innego. Uzyskana frakcja jest nieredukowalna.

Frakcja ¾ jest nieredukowalna, jak wspomniano wcześniej, ponieważ jest ze sobą 3 i 4 kuzynami, ale następująca metoda pozwala na nieskończone frakcje równoważne ¾.

Wzmocnienie

Aby wzmocnić daną frakcję, licznik i mianownik muszą być pomnożone przez tę samą kwotę, bez względu na to, czy jest to liczba dodatnia czy ujemna. Na przykład frakcja 6/8 uzyskano przez amplifikację ¾ według współczynnika 2:

$\frac34=\frac3\times 24\times 2=\frac68$

Chociaż ułamki mają inny licznik i mianownik, oba są takie same.

Zwróć uwagę na poniższy rysunek, który zawiera dwa identyczne kółka, podzielone na równe części, choć różnej wielkości. Ostrożnie obserwując, obszary w kolorze zielonym i fioletowym mają tę samą miarę, ale obszar zielony został podzielony na 3 części, łącznie 4, które tworzą koło lewej. Z drugiej strony okrąg po prawej stronie został podzielony na 8 równych części, a purpurowy obszar jest równoważny 6 z nich.

W ten sposób możesz wykres, że ¾ jest równoważny 6/8, ponieważ oba frakcje reprezentują tę samą kwotę.

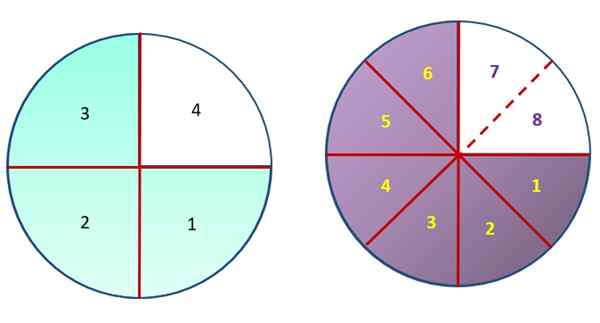Frakcje ¾ i 6/8 reprezentują ten sam obszar w obu kręgach. Źródło: f. Zapata.

Ogólnie rzecz biorąc, jeśli ułamek jest mnożony ¾ przez liczbę n, tak wiele frakcji równoważnych jest z niej uzyskanych, jak chcesz:

$\frac34=\frac3\times n4\times n=\frac3n4n$

Należy zauważyć, że n nigdy nie może być równe 0, ponieważ podział na 0 nie jest zdefiniowany. Żadna frakcja nie może mieć 0 w twoim mianowniku.

Jak wiedzieć, czy ułamek jest równoważny 3/4?

Jak wyjaśniono na początku, sposobem na poznanie, czy ułamek jest równoważny ¾ jest podjęcie ilorazu między licznikiem a mianownikiem. Jeśli jest 0.75, ułamek jest równoważny ¾, ale istnieje kilka kolejnych metod, które nie wymagają bezpośrednio podziału:

Może ci służyć: Media ważone: jak jest obliczane, przykłady i ćwiczenia

Metoda 1

Załóżmy, że ułamek a/b i chcesz wiedzieć, czy jest to równoważne ¾, to znaczy, jeśli to prawda, że:

$\frac34=\fracab$

Aby być równoważnym, produkt 4 musi być równy produktowi 3B:

4a = 3b

Metoda 2

Jeśli ułamek A/B jest równoważny ¾, dzieląc A i B przez jego maksymalny wspólny dzielnik MCD, wynik musi wynosić ¾.

Aby wyjaśnić zastosowanie tych metod, zobacz następujące przykłady.

Przykłady

Przykład 1

Określ, czy ułamek 150/200 jest równoważny ¾:

Metodą 1

W takim przypadku A = 150 i B = 200, należy spełnić, że:

4a = 3b

4 × 150 = 600
3 × 200 = 600

Stwierdzono, że 150 /200 jest równoważne ¾.

Metodą 2

Maksymalny wspólny dzielnik 150 i 300 dzieli je dokładnie. Obie ilości rozkładają się w swoich głównych czynnikach, a następnie powszechne czynniki z ich najmniejszym wykładnikiem są pomnożone:

150 = 2 × 5² × 3
200 = 2³ × 5²

2 i 5 są powszechne, mnożą się wybierając najmniejszą moc, z jaką się pojawiają:

MCD (150, 200) = 2 × 5² = 2 × 25 = 50

Teraz przystępujemy do dzielenia:

$\frac150200=\frac150 \div50 200\div 50=\frac34$

Rozwiązane ćwiczenia

Ćwiczenie 1

Napisz według wzmocnienia pięć frakcji równoważnych ¾, mnożąc licznik i mianownik za każdym razem przez następujące liczby całkowitego:

a) 3, b) 5, c) (-2), d) 10 i e) 20

Rozwiązanie

$\frac3 \times 3 4\times 3=\frac912$

Rozwiązanie b

$\frac3 \times 5 4\times 5=\frac1520$

Rozwiązanie c

$\frac3 \times (-2) 4\times (-2)=\frac-6-8=\frac68$ Zauważ, że nie ma różnicy poprzez wzmocnienie frakcji przez 2 lub -2, ponieważ zgodnie z zasadą znaków iloraz wskazany między dwiema ujemnymi kwotami jest dodatnia.

Rozwiązanie d

$\frac3 \times 10 4\times 10=\frac3040$

Rozwiązanie e

$\frac3 \times 20 4\times 20=\frac6080$ Należy zauważyć, że frakcja ta jest taka sama, jak uzyskana przez wzmacnianie przez 2 ułamek uzyskany powyżej:

$\frac30 \times 2 40\times 2=\frac6080$