Przepływ pola elektrycznego

Co to jest przepływ pola elektrycznego?

On przepływ pola elektrycznego lub po prostu przepływ elektryczny jest ilością skalarną proporcjonalną do liczby linii pola elektrycznego, które przecinają powierzchnię. Jest to oznaczone przez kapitał literowy φ (phi).

Pole elektryczne tak naprawdę nie „przepływa” tak, jak robi to strumień wody, chociaż linie przepływowe płynu przypomina linie pola elektrycznego.

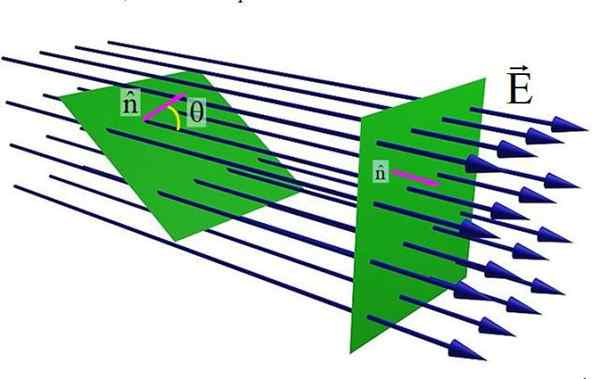
Rysunek 1. Pole elektryczne przepływ przez płaską powierzchnię. Źródło: Wikimedia Commons.

Górna figura pokazuje płaską powierzchnię skrzyżowaną przez pole elektryczne I. Gdy normalny wektor jednostki na powierzchnię N i pole I Są równoległe, ilość linii pola, które przekraczają powierzchnię, jest maksymalna. Ale wraz ze wzrostem kąt θ N I I, Liczba linii przechodzących przez zieloną powierzchnię jest niższa.

Z drugiej strony przepływ pola elektrycznego zależy również od wielkości I, Ponieważ im wyższe to, im więcej linii pola przecinają powierzchnię. I oczywiście im większy obszar S wspomnianej powierzchni, także przepływ, więc ustalono następujące równanie:

Φ = e ∙ sosθ

To wyrażenie jest zgodne z produktem skalarnym wśród wektorów I I N:

Φ = (I • • N) S

Jednostka przepływu pola elektrycznego w międzynarodowym systemie jednostek, jeśli n.M²/C (Newton x Square Metro/Coulomb). Alternatywnie, ponieważ pole jest również mierzone w v/m (wolt na metrze), przepływ elektryczny jest w (v ∙ m) m).

Przykłady

Zgodnie z definicją przepływ elektryczny może być dodatni, ujemny lub równy 0. Przepływ pola elektrycznego to:

Może ci służyć: magnetyzacja: moment magnetyczny orbital i spin, przykłady

-Pozytywny, gdy kąt θ I I N Jest mniej niż 90º, ponieważ cos θ jest większy niż zero.

-Ujemny, jeśli ten kąt jest większy niż 90º, ponieważ wówczas cos θ jest mniejszy niż zero.

-Pustka, gdy θ jest wart dokładnie 90º, ponieważ cos 90º = 0, a linie pola w tym przypadku są styczne do powierzchni.

-Z drugiej strony, jeśli kąt między I I N Jest równy 0, przepływ nabywa maksymalną wartość.

Te możliwości pokazano na poniższym obrazku:

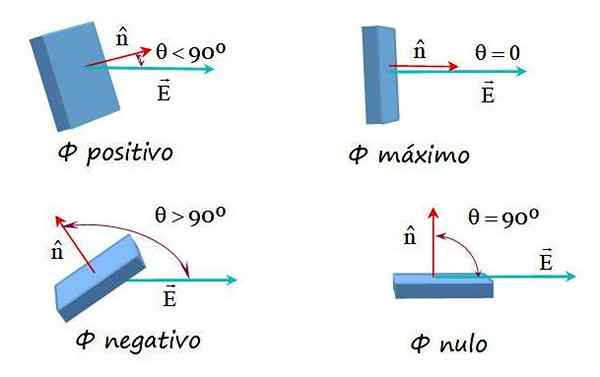Rysunek 2. Przykłady przepływu pola elektrycznego z różnymi orientacjami między polem a normalnym wektorem powierzchniowym. Źródło: f. Zapata.

Pole elektryczne przepływ na dowolnej powierzchni

Wcześniej przepływ pola elektrycznego określono w konkretnym przypadku jednolitego pola wpływającego na płaską powierzchnię. Dla dowolnej powierzchni i/lub niejednorodnego pola elektrycznego kąt między I I N może się różnić od punktu do punktu.

Na poniższym rysunku istnieją dwa przykłady, po lewej zakrzywionej powierzchni i po prawej stronie zamkniętej powierzchni.

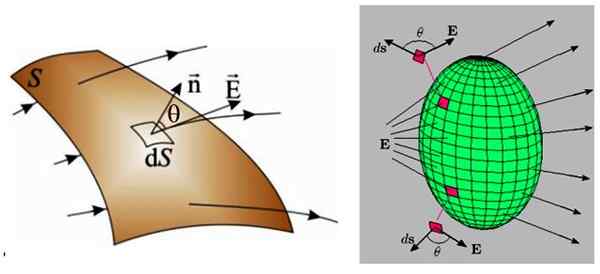Rysunek 3. Po lewej stronie dowolna powierzchnia, na której krzyżuje się nierównomierne pole elektryczne. Po prawej stronie niejednorodne pole elektryczne przecina zamkniętą powierzchnię, dlatego przepływ netto w tym przypadku jest nieważny. Źródło: f. Zapata.

W obu przypadkach powierzchnia jest podzielona na znacznie mniejsze regiony o wielkości nieskończenie małej, zwanej DS, dla których przecina także nieskończenie małe Dna:

dφ = (I• •N) Ds = (ecosθ) ds

Całkowite pole jest uzyskiwane przez dodanie wszystkich tych nieskończenie małym:

Symbol S jako indeks dolny w całce wskazuje, że należy go obliczyć na całej powierzchni. Jeśli jest to zamknięte, jest to oznaczone małym okręgiem na całce:

Może ci służyć: stałe antoine: wzory, równania, przykłady

W przypadku zamkniętych powierzchni, N Zawsze zaznacz, więc przepływ ma znak +, gdy jest wychodzący, ponieważ kąt pomiędzy I I N jest mniej niż 90º i znak - gdy pole jest przychodzące, ponieważ wówczas kąt pomiędzy I I N jest większy niż 90º (patrz rysunek 2).

Zwróć uwagę, że na zamkniętej powierzchni po prawej stronie liczba linii pola, która wchodzi na powierzchnię, jest równa liczbie wychodzących linii. Dlatego przepływ netto, zdefiniowany jako suma algebraiczna przepływu i przepływu wychodzącego, jest nieważny.

Źródło pola elektrycznego w tym przypadku znajduje się poza powierzchnią, jednak przepływ netto byłby różny od 0, gdyby źródło pola elektrycznego (rozkład obciążeń) znajdował się wewnątrz powierzchni.

Ćwiczenia

Ćwiczenie 1

Masz pole elektryczne I = 3.5 kN/c X i płaska prostokątna powierzchnia 0.35 m szerokości na 0.7 m długości. Znajdź przepływ pola elektrycznego, który przecina prostokąt w następujących przypadkach:

a) Powierzchnia jest równoległa do płaszczyzny YZ.

b) prostokąt jest równolegle do płaszczyzny XY.

c) płaszczyzna normalna tworzy kąt 40º z osą x i zawiera oś i.

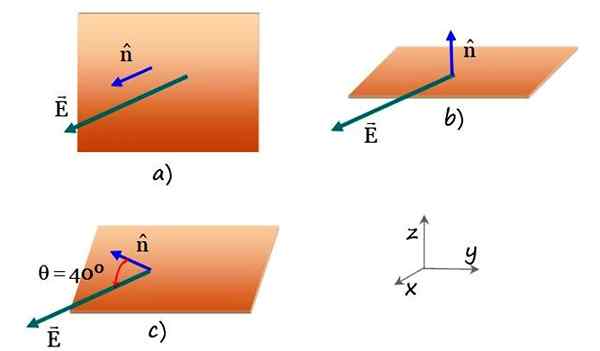Rysunek 4. Prostokątna płaszczyzna skrzyżowana przez jednolite pole elektryczne w różnych orientacjach płaszczyzny. Źródło: f. Zapata.

Rozwiązanie

Normalny wektor i wektor pola elektrycznego są równoległe, dlatego kąt θ między nimi wynosi 0º, a przepływ elektryczny:

Φ = (e ∙ s) cos 0 = e ∙ s

Obszar S prostokąta to:

Może Ci służyć: Metoda równoległobramowa: przykłady, rozwiązane ćwiczenia

S = 0.35 m x 0.7 m = 0.245 m²

Zastąpienie w φ:

Φ = e ∙ s = 3.5 x 10³ N/c × 0.245 m² = 857.5 n ∙ m² /C.

Rozwiązanie b

Przepływ pola elektrycznego wynosi 0, ponieważ wektory I I N Są prostopadłe do siebie.

Rozwiązanie c

Kąt θ między polem I i normalny wektor N jest 40º (patrz rysunek), dlatego:

Φ = e ∙ s ∙ cos θ = 3.5 x 10³ N/c × 0.245 m² × cos 40º = 656.9 n ∙ m² /C.

Ćwiczenie 2

Oblicz przepływ pola elektrycznego, który wytwarza dodatnie obciążenie punktualne_albo = 2 μc znajdujący się w środku kuli promieniowej r = 5 cm.

Rozwiązanie

Pole wytwarzane przez obciążenie Q_albo Nie jest to jednolite, ale z prawa kulombowskiego wiadomo, że na powierzchni kuli ma wielkość:

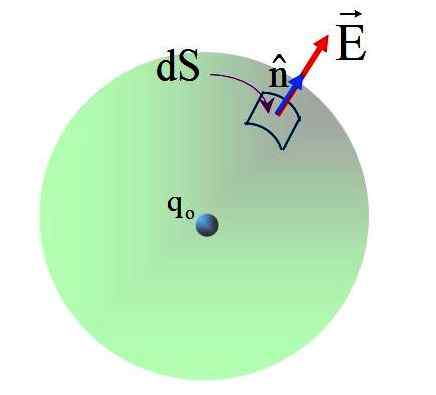Rysunek 5. Muchy pola wytwarzane na powierzchni kuli przez punktualne obciążenie w jej środku. Źródło: f. Zapata.

Pole ma kierunek promieniowy i normalny wektor N, Dlatego kąt między dwoma wektorami wynosi 0 we wszystkich punktach powierzchni sferycznej. Zastąpienie:

Musisz:

Integralą DS na całej sferycznej powierzchni jest jej obszar, który wynosi 4πr^2, W związku z tym:

Co dochodzi do wniosku, że przepływ pola elektrycznego nie zależy od powierzchni, ale od zablokowanego obciążenia.

Jego wartość to:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m²/C = 2.3 x 10⁵ N⋅m²/C

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 5. Elektrostatyka. Pod redakcją Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
4. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. osoba.