Faktoring

Jaka jest czynnikowanie?

Faktoryzacja jest metodą, za pomocą której wyraża się wielomian w postaci mnożenia czynników, które mogą być liczbami, literami lub obiema. W przypadku uwzględnienia czynniki wspólne dla terminów są pogrupowane, i w ten sposób wielomian jest rozkładany w kilku wielomianach.

Zatem, gdy czynniki mnożą się ze sobą, wynikiem jest oryginalny wielomian. Faktoryzacja jest bardzo przydatną metodą, gdy występują wyrażenia algebraiczne, ponieważ może stać się mnożeniem kilku prostych terminów; Na przykład: 2² + 2AB = 2a _* (A + B).

Istnieją przypadki, w których wielomianu nie można rozmiarować, ponieważ nie ma wspólnego czynnika między jego terminami; Zatem te wyrażenia algebraiczne są podzielne tylko między sobą i przez 1. Na przykład: x + y + z.

W wyrażeniu algebraicznym wspólnym czynnikiem jest maksymalny wspólny dzielnik terminów, które go komponują.

Metody czynników

Istnieje kilka metod faktoryzacji, które są stosowane w zależności od przypadku. Niektóre z nich są następujące:

Wspólna czynnik

W tej metodzie zidentyfikowane są te czynniki, które są wspólne; to znaczy ci, którzy są powtarzani w kategoriach wyrażenia. Następnie stosuje się właściwość dystrybucyjna, maksymalny wspólny dzielnik jest usuwany, a faktoryzacja jest zakończona.

Innymi słowy, wspólny czynnik wyrażenia jest zidentyfikowany i każdy termin jest podzielony między to; Powstałe terminy zostaną pomnożone przez maksymalny wspólny dzielnik, aby wyrazić czynnikowanie.

Przykład 1

Forestize (b²x) + (b²I).

Rozwiązanie

Pierwszy to wspólny czynnik każdego terminu, który w tym przypadku jest B², A następnie warunki są podzielone między wspólny czynnik w następujący sposób:

(B²x) / b² = x

(B²y) / b² = y.

Faktoryzacja jest wyrażona, mnożąc wspólny czynnik przez wynikające z nich terminy:

(B²x) + (b²y) = B² (x + y).

Przykład 2

Foregrize (2²B³) + (3AB²).

Rozwiązanie

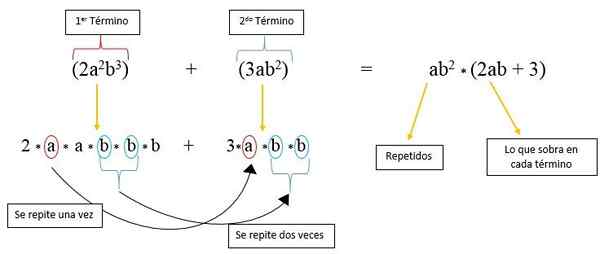
W tym przypadku mamy dwa czynniki powtarzane w każdym terminie, które są „a” i „b”, i które są podniesione do mocy. Aby najpierw je uwzględnić, dwa terminy są rozkładane w ich długiej formie:

2_*Do_*Do_*B_*B_*B + 3a_*B_*B

Można zauważyć, że współczynnik „A” powtarza się tylko raz w drugim okresie, a współczynnik „B” powtarza się w tym dwukrotnie; Tak więc w pierwszym okresie jest tylko 2, czynnik „A” i jeden „B”; Podczas gdy w drugim okresie pozostaje tylko 3.

Dlatego jest napisane tyle razy, ile „A” i „B” są powtarzane i mnożone przez czynniki pozostawione z każdego terminu, jak zaobserwowano na obrazie:

Grupowanie faktorystyki

Ponieważ nie we wszystkich przypadkach maksymalny wspólny dzielnik wielomianu jest wyraźnie wyrażony, konieczne jest podjęcie innych kroków, aby móc przepisać wielomian, a tym samym uwzględnić.

Może ci służyć: sekcje stożkowe: typy, aplikacje, przykłady

Jednym z tych kroków jest grupowanie warunków wielomianu na kilka grup, a następnie użycie metody wspólnej czynników.

Przykład 1

Forestize AC + BC + AD + BD.

Rozwiązanie

Istnieją 4 czynniki, w których dwa są powszechne: w pierwszym semestrze jest to „c”, aw drugim jest „d”. W ten sposób dwa terminy są zgrupowane i oddzielone:

(AC + BC) + (AD + BD).

Teraz możliwe jest zastosowanie metody wspólnego czynnika, dzieląc każdy termin przez jego wspólny czynnik, a następnie pomnożenie tego wspólnego czynnika przez wynikające z tego terminy, takie jak to:

(AC + BC) / C = A + B

(AD + BD) / D = A + B

C (A + B) + D (A + B).

Teraz uzyskuje się dwumianę, która jest powszechna dla obu warunków. Uwzględniać to mnożenie przez pozostałe czynniki; W ten sposób musisz:

AC + BC + AD + BD =  (C + D) _* (A + B).

Faktoralizacja inspekcji

Ta metoda jest stosowana do uwzględnienia kwadratowych wielomianów, zwanych także trynomialami; to znaczy te, które są ustrukturyzowane jako topór² ± bx + c, gdzie wartość „a” różni się od 1. Ta metoda jest również stosowana, gdy trójmian ma kształt x² ± bx + c i wartość „a” = 1.

Przykład 1

Czynnik x² + 5x + 6.

Rozwiązanie

Masz kwadratowy trynomial formy x² ± Bx + C. Aby to uwzględnić, najpierw należy znaleźć dwie liczby, że podczas mnożącego się powoduje wartość „C” (to znaczy 6) i że jej suma jest równa współczynnikowi „B”. Te liczby to 2 i 3:

2 _* 3 = 6

2 + 3 = 5.

W ten sposób wyrażenie jest uproszczone w następujący sposób:

(X² + 2x) + (3x + 6)

Każdy termin jest czynnikiem:

• Dla (x² + 2x) Wspólny termin jest usuwany: x (x + 2)
• Dla (3x + 6) = 3 (x + 2)

Zatem wyrażenie pozostaje:

x (x +2) +3 (x +2).

Ponieważ masz wspólny dwumian, aby zmniejszyć wyrażenie, mnoży to przez resztki terminów i musi:

X² + 5x + 6 = (x + 2) _* (x + 3).

Przykład 2

Factorize 4a² + 12a +9 = 0.

Rozwiązanie

Masz kwadratowy trójmian postaci topora² ± bx + c i uwzględniać to mnożą wszystkie wyrażenie przez współczynnik x²; W tym przypadku 4.

4² + 12a +9 = 0

4² (4) + 12a (4) + 9 (4) = 0 (4)

16 a² + 12a (4) + 36 = 0

4² Do² + 12a (4) + 36 = 0

Teraz należy znaleźć dwie liczby, że podczas mnożenia ze sobą powodują wartość „c” (czyli 36) i że przy łączeniu współczynnika terminu „a”, czyli 6.

6 _* 6 = 36

6 + 6 = 12.

W ten sposób wyrażenie jest przepisane, biorąc pod uwagę 4² Do² = 4a _* 4. Dlatego do każdego terminu stosuje się nieruchomość dystrybucyjną:

Może ci służyć: Mackinder Box

(4a + 6) _* (4a + 6).

Wreszcie wyrażenie jest podzielone przez współczynnik²; To znaczy 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6) / 2) _* ((4a + 6)/ 2).

Wyrażenie jest następujące:

4² + 12a +9 = (2a +3) _* (2a + 3).

Faktoralizacja za pomocą znaczących produktów

Są przypadki, w których całkowicie uwzględniono wielomiany z poprzednimi metodami, staje się to bardzo długi proces.

Dlatego można opracować wyrażenie z formułami godnych uwagi produktów, a zatem proces staje się prostszy. Wśród najbardziej używanych godnych uwagi produktów są:

• Różnica dwóch kwadratów: (A² - B²) = (a - b) _* (A + B)
• Idealny kwadrat suma: a² + 2AB +b² = (A + B)²
• Idealny kwadrat różnicy: a² - 2AB + b² = (a - b)²
• Różnica dwóch kostek: a³ - B³ = (A-B)_*(Do² + AB + B²)
• Suma dwóch kostek: a³ - B³ = (A + B) _* (Do² - AB + B²)

Przykład 1

Foregrize (5² - X²)

Rozwiązanie

W tym przypadku istnieje różnica dwóch kwadratów; Dlatego stosowany jest wzór znaczącego produktu:

(Do² - B²) = (a - b) _* (A + B)

(5² - X²) = (5 - x) _* (5 + x)

Przykład 2

Forestize 16x² + 40x + 25²

Rozwiązanie

W takim przypadku istnieje idealny kwadrat suma, ponieważ można zidentyfikować dwa warunki kwadratowe, a termin pozostawiony jest wynikiem pomnożenia dwóch przez pierwiastek kwadratowy pierwszego terminu, przez pierwiastek kwadratowy drugiego terminu.

Do² + 2AB +b² = (A + B)²

W obliczeniach tylko korzenie kwadratowe pierwszego i trzeciego okresu:

(16x²) = 4x

√ (25²) = 5.

Następnie dwa wynikowe terminy są wyrażane oddzielone znakiem operacji, a cały kwadratowy wielomian jest podwyższony:

16x² + 40x + 25² = (4x + 5)².

Przykład 3

Forestize 27a³ - B³

Rozwiązanie

Wyrażenie reprezentuje odjęcie, w którym dwa czynniki są podwyższone do sześcianu. Aby je uwzględnić, stosuje się formułę znaczącego produktu różnicy w kostkach, czyli:

Do³ - B³ = (A-B)_*(Do² + AB + B²)

Zatem, aby uwzględnić korzeń sześcienny z każdego okresu dwumianowego i mnożony przez kwadrat pierwszego okresu, a także iloczyn pierwszego według drugiego okresu, a także drugi termin kwadratowy.

27a³ - B³

√√ (27a³) = 3a

³√ (-B³) = -B

27a³ - B³ = (3a - b) _* [(3a)² + 3AB + b²)]

27a³ - B³ = (3a - b) _* (9a² + 3AB + b²)

Faktoryzacja z zasadą Ruffini

Ta metoda jest stosowana, gdy masz wielomian stopnia większy niż dwa, aby uprościć wyrażenie do kilku mniejszych wielomianów.

Przykład 1

Factorice q (x) = x⁴ - 9x² + 4x + 12

Rozwiązanie

Najpierw poszukiwane są liczby, które są dzielnikami 12, co jest niezależnym terminem; Są to ± 1, ± 2, ± 3, ± 4, ± 6 i ± 12.

Może ci służyć: wielokrotności 2: co to jest i wyjaśnienie

Następnie x jest zastępowane przez te wartości, od najmniej do największego, a zatem jest on określany, za pomocą której wartości podział będzie dokładny; to znaczy reszta musi wynosić 0:

x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

Q (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

I tak dalej dla każdego dzielnika. W takim przypadku znalezione czynniki dotyczą x = -1 i x = 2.

Metoda Ruffini jest teraz stosowana, zgodnie z którym współczynniki ekspresji zostaną podzielone przez czynniki znalezione, aby podział był dokładny. Warunki wielomianowe są uporządkowane od większego do niższego wykładnika; W przypadku braku terminu wraz z stopniem następującym w sekwencji, 0 umieszcza się na miejscu.

Współczynniki znajdują się na schemacie, jak pokazano na następującym obrazie.

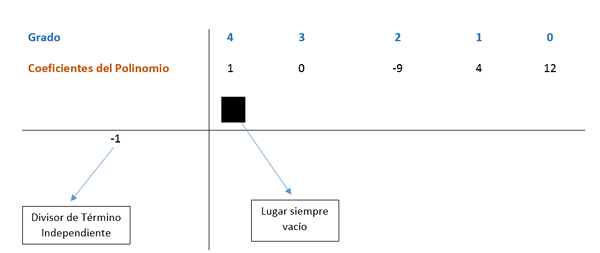
Pierwszy współczynnik jest obniżony i mnożony przez dzielnika. W tym przypadku pierwszy dzielnik to -1, a wynik jest umieszczony w następującej kolumnie. Następnie wartość współczynnika z uzyskanym wynikiem jest dodawana pionowo, a wynik jest umieszczony poniżej. W ten sposób proces powtarza się do ostatniej kolumny.

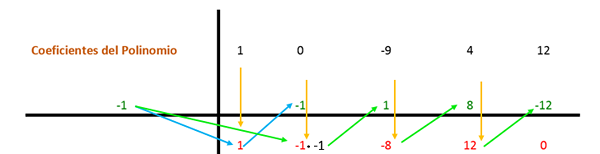
Następnie ta sama procedura jest powtarzana ponownie, ale z drugim dzielnikiem (czyli 2), ponieważ wyrażenie można nadal uprościć.

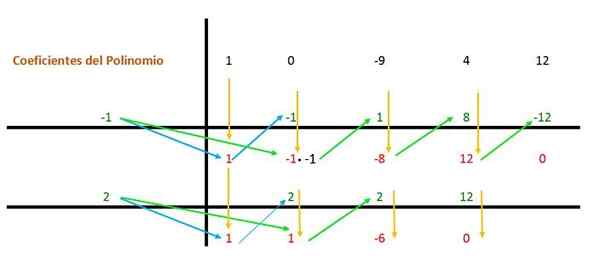
Zatem dla każdego korzenia, wielomian będzie miał termin (x - a), gdzie „a” jest wartością korzenia:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

Z drugiej strony te warunki powinny być pomnożone przez resztę, która pozostała z reguły Ruffini 1: 1 i -6, które są czynnikami reprezentującymi stopień naukowy. W ten sposób formy wyrażenia to: (x² + X - 6).

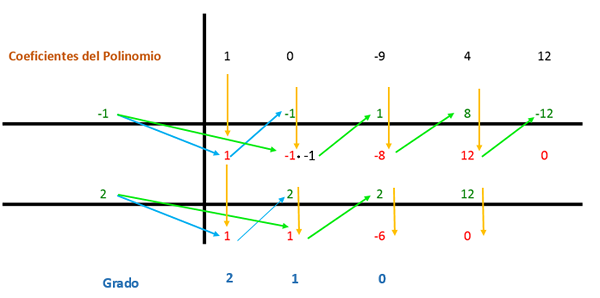
Uzyskanie wyniku faktoralizacji wielomianowej metodą Ruffiniego jest:

X⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (X² + X - 6)

Wreszcie wielomian klasy 2, który pojawia się w poprzednim wyrażeniu, można przepisać jako (x+3) (x-2). Dlatego końcową czynnikiem uwzględniającą:

X⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Bibliografia

1. Arthur Goodman, L. H. (1996). Algebra i trygonometria z geometrią analityczną. Edukacja Pearsona.
2. J, v. (2014). Jak uczyć dzieci o uwzględnieniu wielomianu.
3. Manuel Morillo, a. S. (S.F.). Podstawowa matematyka z aplikacjami.
4. Roelse, s. 1. L. (1997). Liniowe metody wielomianowej faktoralizacji w stosunku do pola skończonych: teoria i implementacje. University Essen.
5. Sharpe, d. (1987). Pierścienie i faktoryzacja.