Współczynnik ściśliwości Jak obliczyć, przykłady i ćwiczenia

On Współczynnik ściśliwości z, o Współczynnik kompresji dla gazów, jest wartością bezwymiarową (bez jednostek), która jest wprowadzana jako korekta w równaniu stanu gazów idealnych. W ten sposób model matematyczny przypomina bardziej obserwowane zachowanie gazu.

W gazie idealnym równanie stanu, które odnosi się do zmiennych P (ciśnienie), V (objętość) i t (temperatura) wynosi: P.V _ideał = n.R.T z n = liczbą moli i r = stała gazów idealnych. Dodając korektę współczynnika kompresji Z, równanie to jest przekształcane w:

P.V = z.N.R.T

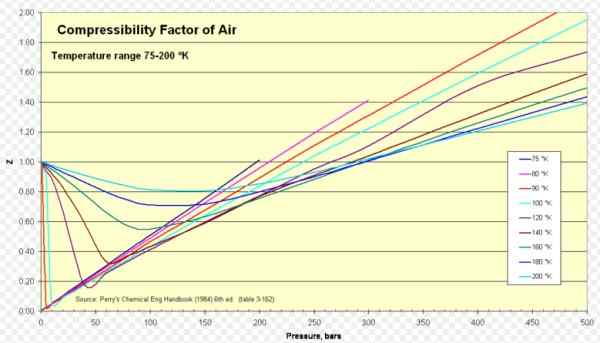
Rysunek 1. Współczynnik ściśliwości powietrza. Źródło: Wikimedia Commons. https: // prześlij.Wikimedia.org/wikipedia/commons/8/84/Cortspressibility_factor_of_air_75-200_k.Png.

[TOC]

Jak obliczyć współczynnik ściśliwości?

Biorąc pod uwagę, że wolumen molowy jest V_Fajny = V/n, Masz prawdziwą objętość molową:

P . V_prawdziwy = Z. R. T → Z = PV _prawdziwy/Rt

Ponieważ współczynnik ściśliwości Z zależy od warunków gazowych, jest wyrażany jako funkcja ciśnienia i temperatury:

Z = z (p, t)

Porównując pierwsze dwa równania, zauważa się, że jeśli liczba moli n jest równa 1, objętość molowa prawdziwego gazu jest związana z objętością gazu idealnego przez:

V_prawdziwy / V_ideał = Z → v _prawdziwy = Z v_ideał

Gdy ciśnienie przekracza 3 atmosfery, większość gazów przestaje zachować się jak gazy idealne, a rzeczywistą objętość różni się znacznie od ideału.

To zrealizowało w jego eksperymentach holenderski fizyk Johannes van der Waals (1837–1923), co doprowadziło go do stworzenia modelu, który lepiej dostosował się do wyników praktycznych niż równanie gazów idealnych: równanie stanu Van der Waalsa.

Może ci służyć: szczawian sodu (Na2C2O4): struktura, właściwości, zastosowania, ryzyko

Przykłady

Zgodnie z równaniem P.V_prawdziwy= Z.N.Rt, Dla gazu idealnego z = 1. Jednak w prawdziwych gazach poprzez zwiększenie ciśnienia wykonuje również wartość z. Ma to sens, ponieważ przy większym ciśnieniu cząsteczki gazu mają więcej możliwości zderzenia, dlatego siły odpychania rosną, a tym samym objętość.

Z drugiej strony do niższych ciśnień, cząsteczki poruszają się z większą swobodą, a siły odpychania zmniejszają. Dlatego oczekuje się niższej objętości. Jeśli chodzi o temperaturę, gdy wzrasta, Z maleje.

Jak zauważył van der Waals, w pobliżu SO -Caled Critical Punkt, zachowanie gazowe jest bardzo odwrócone z gazu idealnego.

Punkt krytyczny (t_C, P_C) dowolnej substancji są wartości ciśnienia i temperatury, które określają ich zachowanie przed zmianą fazy:

-T_C Jest to temperatura, powyżej, dany gaz nie jest upłynniony.

-P_C  Jest to minimalne ciśnienie wymagane do upłynnienia gazu w temperaturze t_C

Każdy gaz ma jednak swój własny punkt krytyczny, definiując temperaturę i zmniejszone ciśnienie t_R I p_R następująco:

P_R = P / p_C

V_R = V /v_C

T_R = T /t_C

Obserwuje się, że gaz ograniczony do identycznych V_R I T_R wywierać ten sam ciśnienie P_R. Z tego powodu, jeśli Z jest graficzny w zależności od P_R do tego samego T_R, Każdy punkt w tej krzywej jest taki sam dla każdego gazu. To się nazywa Zasada odpowiednich stanów.

Współczynnik ściśliwości w gazach idealnych, powietrza, wodoru i wodzie

Poniżej znajduje się krzywa ściśliwości dla różnych gazów w różnych zmniejszonych temperaturach. Następnie kilka przykładów Z dla niektórych gazów i procedury do znalezienia Z za pomocą krzywej.

Może ci służyć: wodór: historia, struktura, właściwości i zastosowania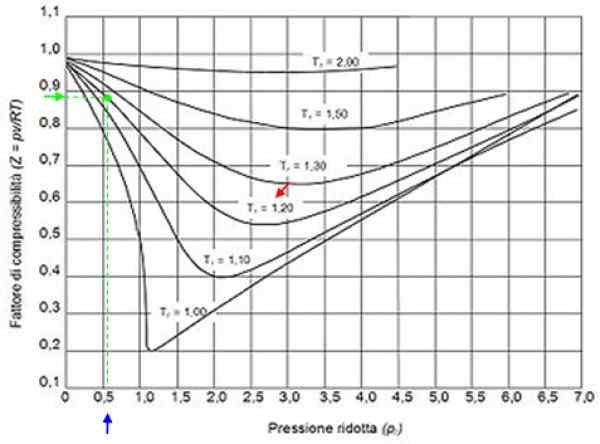Rysunek 2. Grafika graficzna grafiki dla gazów zgodnie z ciśnieniem redukcyjnym. Źródło: Wikimedia Commons.

Gazy idealne

Gazy idealne mają z = 1, jak wyjaśniono na początku.

Powietrze

Dla powietrza Z wynosi około 1 w szerokim zakresie temperatur i ciśnień (patrz ryc. 1), w którym model idealnego gazu daje bardzo dobre wyniki.

Wodór

Z> 1 dla wszystkich ciśnień.

Woda

Aby znaleźć Z wody, potrzebne są wartości punktu krytycznego. Krytycznym punktem wody jest: P_C = 22.09 MPA i T_C= 374.14 ° C (647.3 K). Ponownie należy wziąć pod uwagę, że współczynnik ściśliwości Z zależy od temperatury i ciśnienia.

Załóżmy na przykład, że chcesz znaleźć Z z wody w temperaturze 500 ° C i 12 MPa. Następnie pierwszy jest obliczenie obniżonej temperatury, dla których stopnie Celsjusza należy przekazać Kelvinowi: 50 ºC = 773 K:

T_R = 773/647.3 = 1.2

P_R = 12/22.09 = 0.54

Z tymi wartościami lokalizujemy na wykresie rysunku krzywa odpowiadająca t_R = 1.2, wskazane z czerwoną strzałką. Następnie patrzymy w osi poziomej wartości p_R bliżej 0.54, zaznaczone na niebiesko. Teraz rysujemy pionowo, aż do przechwytywania krzywej T_R = 1.2 i wreszcie jest rzutowane od tego momentu do osi pionowej, gdzie odczytujemy przybliżoną wartość Z = 0.89.

Rozwiązane ćwiczenia

Ćwiczenie 1

Istnieje próbka gazu w temperaturze 350 K i ciśnienie 12 atmosfery, z objętością molową o 12 % wyższą niż przewidywana przez prawo gazów idealnych. Oblicz:

a) współczynnik kompresji Z.

b) Objętość molowa gazu.

Może ci służyć: nieodwracalna reakcja: cechy i przykłady

c) Zgodnie z powyższymi wynikami wskazuj, które są dominującymi siłami w tej próbce gazowej.

Dane: r = 0,082 l.ATM/MOL.K

Rozwiązanie

Znając to v _prawdziwy  jest o 12 % wyższy niż V_ideał :

V_prawdziwy  = 1.12v_ideał

Z = v _prawdziwy / V_ideał = 1.12

Rozwiązanie b

P . V_prawdziwy = Z. R. T → V_prawdziwy = (1.12 x 0.082 x 350 /12) L /mol = 2.14 l/mol.

Rozwiązanie c

Siły odpychania to te, które dominują, ponieważ objętość próbki wzrosła.

Ćwiczenie 2

Istnieje 10 moli etanu ograniczonych w objętości 4.86 L A 27 ºC. Znajdź ciśnienie wywierane przez etan z:

a) Model gazu idealnego

b) równanie van der waals

c) Znajdź współczynnik kompresji z poprzednich wyników.

Dane dla etanu

Van der Waals Współczynniki:

A = 5.489 DM⁶. bankomat . mol^-2  i b = 0.06380 DM³. mol^-1.

Presja krytyczna: 49 atm. Temperatura krytyczna: 305 K

Rozwiązanie

Temperatura jest przekazywana do Kelvina: 27 º C = 27 +273 K = 300 K, pamiętaj również, że 1 litr = 1 l = 1 dm³.

Następnie wymieniono dane dostarczone w równaniu gazowym:

P.V = n.R.T → P = (10 x 0,082 x 300/4.86 L) ATM = 50.6 atm

Rozwiązanie b

Równanie stanu Van der Waals to:

Gdzie A i B są współczynnikami podawanymi przez stwierdzenie. Podczas oczyszczania P:

Rozwiązanie c

Obliczamy zmniejszone ciśnienie i temperaturę:

P_R = 35.2/49 = 0.72

T_R = 300 /305 = 0.98 ≈ 1

Przy tych wartościach poszukiwana jest wartość Z na wykresie na ryc. 2, stwierdzenie, że Z wynosi około 0.7.

 Bibliografia

1. Atkins, str. 1999. Chemia fizyczna. Omega Editions.
2. Cengel i. 2012. Termodynamika. 7^mama Wydanie. McGraw Hill.
3. Engel, t. 2007. Wprowadzenie do fizykochemii: termodynamika. osoba.
4. Levine, ja. 2014. Zasady chemii fizyki. 6th. Wydanie. McGraw Hill.
5. Wikipedia. Współczynnik ściśliwości. Źródło: w:.Wikipedia.org.