Wspólne charakterystyka czynnika, przykłady, ćwiczenia

On wspólny czynnik wyrażenia algebraicznego to kwota, która jest obecna na wszystkich warunkach. Gdy znany jest wspólny czynnik, możliwe jest napisanie wyrażenia w równoważny sposób przez iloczyn czynników.

Nie wszystkie wyrażenia algebraiczne mają wspólny czynnik, istnieją tylko te, które można podzielić tylko między nimi i 1, dlatego nie można ich napisać jako produktu czynników. Przykładem wyrażenia, który nie ma wspólnego czynnika, jest:

x + y

Rysunek 1. Wspólny czynnik ekspresji algebraicznej czyni go wskazanym produktem dwóch czynników. Źródło: Pixabay.

Zamiast tego tak:

5a + 10b

Widać, że 5 jest obecny w obu kategoriach, ponieważ 10 = 5 ∙ 2. Ponieważ 5 jest wspólnym czynnikiem, można zapisać następujące:

5a + 10b = 5 ∙ (A + 2B)

Czytelnik może sprawdzić właściwość dystrybucyjną, że wyrażenie po prawej stronie jest równe oryginałowi.

Wspólnym czynnikiem może być również dosłowny lub kombinacja liczb i liter, na przykład 4x² - 2x. X i 2 Są między czynnikami, a wyrażenie pozostaje jako produkt:

4x² -2x = 2x⋅ (x -1)

Zaletą znalezienia wspólnego czynnika wyrażenia i napisania go jako produktu jest to, że prawie zawsze jest łatwo z nim działać. Dlatego jest stosowany w wielu procedurach algebraicznych i obliczeń, takich jak:

-Podczas rozwiązywania równań, których rozwiązania są szybko ujawnione, gdy znaleziono wspólny czynnik.

-Przy obliczaniu limitu z nieokreślonością może to zniknąć poprzez prawidłowe uwzględnienie.

-Odpowiednia faktoryzacja ułatwia także operacje z wymiernymi wyrażeniami algebraicznymi, takimi jak sumy i odejmowanie.

[TOC]

Wspólne charakterystyki czynnika

Główne cechy wspólnego czynnika są następujące:

-Może to być liczba, wyrażenie algebraiczne lub kombinacja obu.

-Wspólny czynnik musi być zawarty w każdym z terminów wyrażenia do czynnika.

Może ci służyć: funkcje transcendentne: typy, definicja, właściwości, przykłady

-Zgodnie z kwotą zawieranych przez nich warunków może być tak:

1. Wspólny czynnik monomialny, jeśli wspólny czynnik jest jednym terminem,
2. Wspólny czynnik dwumianowy, jeśli masz dwa terminy i
3. Wspólny czynnik wielomianowy, jeśli wspólny czynnik składa się z kilku terminów.

Jak znaleźć wspólny czynnik ekspresji algebraicznej?

Aby znaleźć wspólny czynnik obecny w wielomianie, musisz obliczyć maksymalny wspólny dzielnik lub MCD współczynników numerycznych wszystkich terminów, a także liter lub literały każdego terminu i wybrać moc z najmniejszym wykładnikiem.

Litery lub literały mogą być prezentowane jako monomile, dwumianki lub wielomiany, co będzie widać w poniższych przykładach.

Najbardziej zalecane w celu zrozumienia procesu uzyskania wspólnego czynnika jest przestrzeganie przykładów i ćwiczenie rozwiązywania kilku ćwiczeń w każdym przypadku.

Wspólne przykłady czynników

Nie możemy stracić z oczu faktu, że cel wspólnego czynnika jest przekształcony w wyrażenie na wskazany produkt czynników. Następnie analizowane są najbardziej odpowiednie przypadki:

Wspólny czynnik monomialny

Masz następujące monomile (jedno- wyrażenia algebraiczne):

2x²; 10x⁴I; 100x⁶I²

Co może być wspólnym czynnikiem dla tych trzech?

Zaczynając od współczynników numerycznych: 2, 10 i 100, wszystkie są równe, a ich MCD to 2. Jeśli chodzi o część dosłowną, zmienna x jest obecna w trzech terminach, a najniższa moc to x², Zatem wspólnym czynnikiem jest 2x².

Trzy proponowane warunki można zapisać jako produkty tego czynnika w ten sposób:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²I

100x⁶I²= 2x²∙ 50x⁴I²

Mnożenie czynników po prawej stronie można zweryfikować, że termin po lewej.

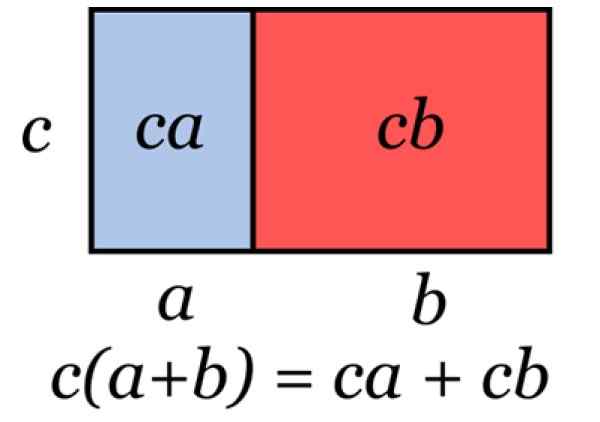Rysunek 2. Ilustracja reprezentuje wspólny czynnik. Źródło: Wikimedia Commons.

Ta technika jest stosowana, gdy jest potrzebna do uwzględnienia wyrażenia algebraicznego, jak w następujących przykładach:

• Przykład 1

Fakt następujące wyrażenie:

Może ci służyć: trójkąt Isosceles

5x³i + 10x²I² + 5xy²

MCD współczynników numerycznych każdego terminu to:

MCD (5.10) = 5

Co do części dosłownej, oba X jak I Są one obecne w trzech warunkach, a najmniej wykładnikowy jest 1, dlatego wspólnym czynnikiem jest 5xy I możesz napisać:

5x³i + 10x²I² + 5xy²= 5xy ∙ (x² +2xy²+I)

Wspólny czynnik wielomianowy

Wspólny czynnik może składać się z dwumianowego, trynomianu lub ogólnie w wielomianowym. W takim przypadku instrukcje w poprzedniej sekcji są nadal ważne, wybierając jako wspólny czynnik ten z najmniejszym wykładnikiem.

• Przykład 2

Napisz następujące wyrażenie jako iloczyn dwóch czynników:

2a (x - 1) - 3b (x -1)

Przez bezpośrednią kontrolę wspólnym czynnikiem jest dwumianowy (X-1), Więc:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Foregharyzacja poprzez grupowanie warunków

Czasami istnienie wspólnego czynnika nie jest oczywiste, ale ujawnia się, czy warunki są zgrupowane w wygodny sposób:

• Przykład 3

Forestize 3x³ - 9ax² - x + 3a

Na pierwszy rzut oka nie ma wspólnego czynnika w tych czterech terminach, ponieważ na przykład X Jest obecny w pierwszych trzech, ale nie w ostatnim. I Do To jest w drugim i w ostatnim nic więcej.

Jeśli chodzi o współczynniki, istnieją trzy terminy, w których 3 jest obecny, jednak jako wspólny czynnik, powinien być pod każdym względem.

Wydaje się, że tym razem opisanych technik nie można zastosować. Jednak wyrażenie może być uwzględnione poprzez grupowanie dwóch pierwszych terminów i dwóch ostatnich, zachowując ostrożność podczas umieszczania nawiasu, że znaki są właściwe, aby nie zmienić oryginału:

Może ci służyć: prostokątne elementy wektora (z ćwiczeniami)

3x³ - 9ax² - x + 3a = (3x³ - 9ax²) - (x - 3a)

Zwróć uwagę na znak ujemny pośród nawiasów: jest to konieczne, ponieważ w przeciwnym razie oryginalne wyrażenie się zmieniło.

W lewym nawiasie wspólnym czynnikiem jest 3x², W związku z tym:

(3x³ - 9ax²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

I obserwuje się, że pojawił się już wspólny czynnik: (x - 3a), Oznacza to, że jest to czynnik po raz drugi, aby uzyskać:

3x² (X- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Wspólne ćwiczenia czynnikowe

Ćwiczenie 1

Rozwiąż równanie 4x³ +7x²  +6x = 0

Rozwiązanie

„X” jest zatem powszechnym czynnikiem:

3x³ −5x²  +2x = x (3x² −5x +2) = 0

W wyrażeniu po lewej, wynosi 0, wystarczy, że jeden z tych dwóch warunków został spełniony:

x = 0

ALBO:

3x² −5x +2 = 0

Jest to kompletne równanie drugiego stopnia, które można rozwiązać, stosując formułę ogólną, również przy użyciu kalkulatora naukowego lub innej metody algebraicznej. Rozwiązania tego równania to:

x = 1

x = 2/3

Po znalezieniu ilustrujące jest napisanie równania jako iloczynu 3 czynników, chociaż stwierdzenie nie poprosiło o to. Byłoby tak:

x⋅ (x-1) ⋅ (x-2/3) = 0

Ćwiczenie 2

Oblicz następujący limit, jeśli istnieje:

Rozwiązanie

Najpierw zastępuje się go na x = −2, aby ocenić limit, w ten sposób jest uzyskiwany:

Ponieważ jest to nieokreśloność formularza 0/0, musisz być czynnikiem, aby spróbować go wyeliminować. Mianownik nie może być czynnikiem, ale licznik tak.

W liczniku wspólnym czynnikiem jest X:

X²+2x = x ∙ (x+2)

Ekspresja faktoryzowana jest zastąpiona w granicy i w ten sposób znika nieokreśloność:

Stwierdzono, że limit istnieje i jest wart -2.

Bibliografia

1. Baldor, a. 2005. Algebra. Grupa kulturowej ojczyzny.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Larson, r. 2012. Przedłużanie. 8. Wydanie. Cengage Learning.
4. Stewart, J. 2007. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.