Czy istnieją trójkąty skalene z kątem prostym?

Istnieje wiele trójkątów Scale o kątu prostym. Przed awansem na ten temat najpierw konieczne jest poznanie różnych rodzajów istnieje trójkąty. Trójkąty są klasyfikowane według dwóch klas: ich wewnętrznych kątów i długości ich boków.

Suma wewnętrznych kątów dowolnego trójkąta jest zawsze równa 180º. Ale zgodnie z kątami wewnętrznymi miary są klasyfikowane jako:

-Acutangle: Te trójkąty są takie, że ich trzy kąty są ostre, to znaczy mierzą mniej niż 90 °.

-Prostokąt: Są to te trójkąty, które mają kąt prosty, to znaczy kąt mierzący 90 °, a zatem pozostałe dwa kąty są ostre.

-Rozwarty: Są to trójkąty, które mają rozwarty kąt, to znaczy kąt, którego miara jest większa niż 90 °.

Trójkąty Scalana z kątem prostym

Zainteresowanie tą częścią polega na ustaleniu, czy trójkąt skaleny może mieć kąt prosty.

Jak powiedziano powyżej, kąt prosty jest kątem, którego miara wynosi 90º. Konieczne jest tylko znanie definicji trójkąta skalenicznego, który zależy od długości boków trójkąta.

Klasyfikacja trójkątów według ich boków

Zgodnie z długością ich boków trójkąty są klasyfikowane jako:

-Równoboczny: Wszystkie te trójkąty, tak że długości ich trzech stron są takie same.

-Równoramienny: Są trójkątami, które mają dokładnie dwie strony o równej długości.

-Różnoboczny: Są te trójkąty, na których trzy strony mają różne miary.

Sformułowanie równoważnego pytania

Pytanie równoważne tytułu brzmi: „Czy istnieją trójkąty, które mają wszystkie trzy strony o różnych miarach, co ma kąt 90 °?"

Odpowiedź, jak stwierdzono na początku, brzmi tak. Nie jest trudno uzasadnić tę odpowiedź.

Jeśli jest starannie zaobserwowany, żaden trójkąt prostokąta nie jest równoboczny, można to uzasadnić dzięki twierdzeniu Pitagorasa dla trójkątów prostokątnych, które mówi:

Biorąc pod uwagę trójkąt prostokąta, że ​​długości ich kategorii to „A” i „B”, a długość jej przeciwprostokątnej wynosi „C”, musisz c² = A²+B², co można zauważyć, że długość przeciwpotrzębienia ” C "jest zawsze większy niż długość każdej nogi.

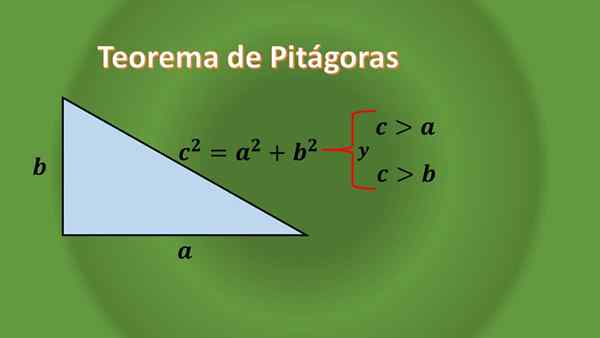
Ponieważ nic nie mówi się o „A” i „B”, oznacza to, że prawym trójkątem może być izosceles lub skalene.

Następnie wybierz po prostu dowolny trójkąt prostokąta, aby jego nogi miały różne miary, a zatem wybrano trójkąt skalenowy, który ma kąt prosty.

Przykłady

-Jeśli rozważany jest trójkąt prostokąta, którego nogi mają długość odpowiednio 3 i 4, wówczas twierdzeniem Pitagoras można stwierdzić, że hipotencja będzie miała długość 5. Oznacza to, że trójkąt jest skalene i ma kąt prosty.

-Niech ABC będzie trójkątem prostokąta z pomiarami pomiarów 1 i 2. Wówczas długość przeciwprostokątnej wynosi √5, co stwierdza, że ​​ABC jest trójkątem prostokąta skalenicznym.

Nie każdy trójkąt skali ma kąt prosty. Można rozważyć trójkąt jak z poniższej figury, która jest salene, ale żaden z jego wewnętrznych kąta nie jest prosty.

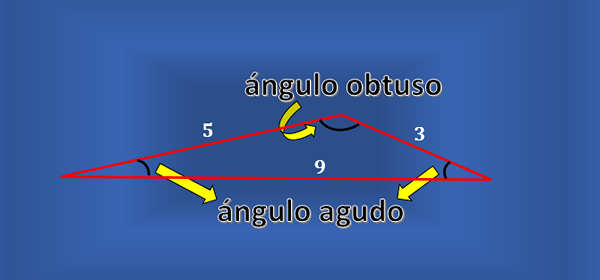Ponadto nie każdy prawy trójkąt jest skaleny. Jeśli weźmiesz pod uwagę prawy trójkąt, którego nogi mierzą oba 1, wówczas hipotencja będzie miała miarę √2. Dlatego trójkąt prostokąta to izosceles.