Równania równowagi termicznej, zastosowania, ćwiczenia

Bilans termiczny dwóch ciał w kontakcie termicznym to stan osiągnięty po wystarczająco długim czasie, aby temperatury obu ciał były równe.

W termodynamice kontakt termiczny dwóch ciał (lub dwóch układów termodynamicznych) jest rozumiany jako sytuacja, w której ciała mają styk mechaniczny lub są oddzielone, ale w kontakcie z powierzchnią, która pozwala tylko przejść ciepła z jednego korpusu do drugiego (powierzchnia diterermiczna (powierzchnia ditericermiczna ).

Rysunek 1. Po chwili lód i napój osiągną równowagę termiczną. Źródło: Pixabay

W kontakcie termicznym nie powinno być reakcji chemicznej między systemami w kontakcie. Powinna być tylko wymiana ciepła.

Codzienne sytuacje, w których występuje wymiana ciepła, są takie systemy takie jak zimny napój i szkło, gorąca kawa i łyżeczka lub ciało i termometr, wśród wielu innych przykładów.

[TOC]

Gdy dwa lub więcej systemów jest w równowadze termicznej?

Drugie prawo termodynamiki określa, że ​​ciepło zawsze przechodzi z najwyższej temperatury do najniższej temperatury. Przenoszenie ciepła ustaje, gdy tylko temperatury zostaną wyrównane i osiągnięto status równowagi termicznej.

Praktyczne zastosowanie równowagi termicznej to termometr. Termometr to urządzenie, które mierzy własną temperaturę, ale dzięki bilansowi termicznemu możemy znać temperaturę innych ciał, takich jak temperatura osoby lub zwierzęcia.

Termometr kolumny rtęci jest umieszczony w kontakcie termicznym z korpusem, na przykład pod językiem, a wystarczająco dużo czasu osiągnie równowagę termiczną między korpusem a termometrem, a jego odczyt nie różni się bardziej.

Po osiągnięciu tego punktu temperatura termometru jest taka sama jak korpus.

Zerowe prawo termodynamiki określa, że ​​jeśli ciało A jest w równowadze termicznej z korpusem C i tym samym korpusem C jest w równowadze termicznej z B, wówczas A i B są w równowadze termicznej, nawet gdy między A i B nie ma kontaktu termicznego.

Dochodzimy do wniosku, że dwa lub więcej układów jest w równowadze termicznej, gdy mają one tę samą temperaturę.

Równania równowagi termicznej

Zakładamy korpus w początkowej temperaturze w kontakcie termicznym z innym korpusem B z początkową temperaturą TB. Zakładamy również, że TA> TB, a następnie zgodnie z drugim prawem ciepło jest przenoszone z A na B.

Po chwili osiągnięto równowagę termiczną, a oba ciała będą miały tę samą końcową temperaturę TF. Będzie to miało wartość pośredniego do TA i TB, to znaczy ta> tf> tb.

Ilość ciepła przeniesionego z A do B wyniesie Qa = Ma Ca (Tf - TA), gdzie MA jest masą ciała A, Ca Ca Pojemność cieplna na jednostkę masy y (tf - ta) różnica temperatur. Jeśli TF jest mniejsza niż wtedy, QA jest ujemne, co wskazuje, że ciało daje ciepło.

Podobnie dla ciała B musisz QB = MB CB (TF - TB); A jeśli TF jest większy niż TB, QB jest dodatni, wskazując, że ciało B odbiera ciepło. Ponieważ ciało A i B są w kontakcie termicznym między nimi, ale odizolowane od środowiska, całkowita ilość wymienionego ciepła powinna być zerowa: QA + QB = 0

Następnie Ma Ca (TF - TA) + MB CB (TF - TB) = 0

Temperatura równowagi

Opracowując tę ​​ekspresję i usuwając temperaturę TF, otrzymuje się końcową temperaturę równowagi termicznej.

Rysunek 2. Temperatura równowagi końcowej. Źródło: Self Made

Tf = (ma ca ta + mb cb tb) / (ma ca + mb cb).

Jako szczególny przypadek, rozważ przypadek, że ciała A i B są identyczne pod względem masy i pojemności cieplnej, w tym przypadku temperatury równowagi będzie:

Tf = (ta + tb) / 2 ↔ Jeśli ma = mb i ca = cb.

Kontakt termiczny ze zmianą fazową

W niektórych sytuacjach zdarza się, że gdy dwa ciała są umieszczone w kontakcie termicznym, wymiana ciepła powoduje zmianę stanu lub fazy w jednym z nich. Jeśli tak się stanie, należy wziąć pod uwagę, że podczas zmiany fazy nie ma zmiany temperatury w ciele, która modyfikuje jego status.

Jeśli nastąpi zmiana fazowa jednego z ciał w kontakcie termicznym, zastosowana jest pojęcie utajonego ciepła L, która jest energią na jednostkę masy niezbędnej do zmiany stanu:

Q = l ∙ m

Na przykład, aby stopić 1 kg lodu w 0 ° C, wymagane są 333,5 kJ/kg, a wartość ta jest utajonym ciepłem topnienia lodu.

Podczas fuzji woda stała jest zmieniana na ciekłą wodę, ale ta woda utrzymuje tę samą temperaturę lodowcową podczas procesu fuzji.

Aplikacje

Bilans termiczny jest częścią codziennego życia. Na przykład zbadajmy szczegółowo tę sytuację:

-Ćwiczenie 1

Osoba chce kąpać się z ciepłą wodą w temperaturze 25 ° C. W kostce umieszcza 3 litrów zimnej wody w 15 ° C, a w kuchennej wodzie cieplnej do 95 ° C.

Ile litrów gorącej wody musi dodać do kostki zimnej wody, aby mieć pożądaną końcową temperaturę?

Rozwiązanie

Załóżmy, że jest to zimna woda i gorąca woda:

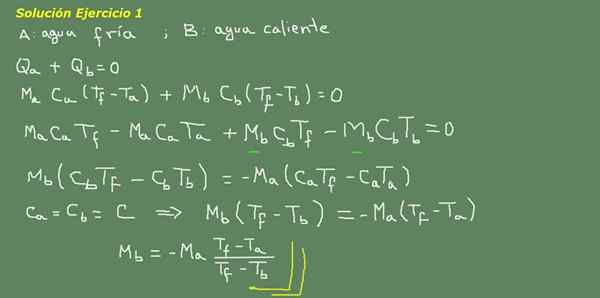Rysunek 3. Ćwiczenie 3 Rozwiązanie. Źródło: Self Made.

Proponujemy równanie równowagi termicznej, jak wskazano na tablicy na rycinie 3, a stamtąd usuwamy wodę MB.

Początkową masę zimnej wody można uzyskać, ponieważ znana jest gęstość wody, która wynosi 1 kg dla każdego litra. To znaczy mamy 3 kg zimnej wody.

Ma = 3 kg

Więc

MB = - 3 kg*(25 ° C - 15 ° C)/(25 ° C - 95 ° C) = 0,43 kg

Następnie wystarczy 0,43 lts gorącej wody, aby w końcu uzyskać 3,43 litrów ciepłej wody w temperaturze 25 ° C.

Rozwiązane ćwiczenia

-Ćwiczenie 2

Wprowadzono kawałek metalu o masie 150 g i o temperaturze 95 ° C do pojemnika zawierającego pół litra wody w temperaturze 18 ° C. Po chwili osiągnięto równowagę termiczną i temperaturę wody i metalu wynosi 25 ° C.

Załóżmy, że pojemnik z wodą i metalowym kawałkiem jest zamkniętym termosem, który nie pozwala na wymianę ciepła w środowisku.

Uzyskaj ciepło właściwe metalu.

Rozwiązanie

Najpierw obliczymy ciepło pochłaniane przez wodę:

QA = MA CA (TF - TA)

QA = 500 g 1cal/(G ° C) (25 ° C - 18 ° C) = 3500 kalorii.

To jest to samo ciepło podane przez metalu:

QM = 150 g cm (25 ° C - 95 ° C) = -3500 kalorii.

Następnie możemy uzyskać pojemność cieplną metalu:

CM = 3500 CAL/ (150G 70 ° C) = ⅓ Cal/ (G ° C).

Ćwiczenie 3

Masz 250 c.C. wody w 30 ° C. Do tej wody, która znajduje się w termosie izolacyjnym, dodaje się 25 g kostek lodu w 0 ° C, w celu chłodzenia.

Określić temperaturę równowagi; to znaczy temperatura, która pozostanie, gdy cały lód się stopi, a woda lodowa ogrzeje, aż woda, która początkowo miała szkło.

Rozwiązanie 3

To ćwiczenie można rozwiązać w trzech etapach:

1. Pierwszym z nich jest fuzja lodu, która pochłania ciepło z początkowej wody, aby się stopić i stać się wodą.
2. Następnie obliczany jest spadek temperatury w początkowej wodzie, ponieważ podał ciepło (Qcede<0) para fundir el hielo.
3. Wreszcie, stopiona woda (z lodu) musi być zrównoważona termicznie z wodą, która początkowo istniała.

Rysunek 4. Ćwiczenie 3 Rozwiązanie. Źródło: Self Made.

Obliczmy ciepło niezbędne do połączenia lodu:

Qf = l * MH = 333,5 kJ/kg * 0,025 kg = 8338 kJ

Następnie ciepło przypisane przez wodę do stopienia lodu jest qced = -qf

To ciepło przypisane przez wodę schodzi jej temperatury do wartości T, którą możemy obliczyć w następujący sposób:

T '= t0 - qf/(ma*ca) = 22,02 ° C

Gdzie CA jest pojemnością cieplną wody: 4,18 kJ/(kg ° C).

Wreszcie pierwotna masa wody, która jest obecnie w 22,02 ° C, da ciepło do stopionej wody z lodu, która wynosi 0 ° C.

Wreszcie temperatura równowagi zostanie osiągnięta po wystarczającym czasie:

Te = (ma * t ' + mh * 0 ° c) / (ma + mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg).

Wreszcie uzyskanie temperatury równowagi:

TE = 20,02 ° C.

-Ćwiczenie 4

Kawałek o długości 0,5 kg pozostawia piekarnik w temperaturze 150 ° C, który jest znacznie poniżej jego temperatury topnienia. Ten kawałek jest umieszczony w pojemniku z 3 litrami wody w temperaturze pokojowej 20 ° C. Określ końcową temperaturę równowagi.

Oblicz także:

- Ilość ciepła dostarczanego przez prowadzenie do wody.

- Ilość ciepła wchłaniana przez wodę.

Dane:

Specyficzne ciepło ołowiu: CP = 0,03 wapna/(G ° C); Specyficzne ciepło wody: CA = 1 wapno/(g ° C).

Rozwiązanie 

Po pierwsze, określamy końcową temperaturę równowagi TE:

Te = (ma ca ta + mp cp tp) / (ma ca + mp cp)

TE = 20,65 ° C

Wówczas ilość ciepła przypisanego przez ołów wynosi:

QP = MP CP (TE - TP) = -1,94 x 10³ wapno.

Ilość ciepła pochłoniętego przez wodę będzie:

QA = MA CA (TE - TA) = +1,94x 10³ wapna.

Bibliografia

1. Atkins, str. 1999. Chemia fizyczna. Omega Editions.
2. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
3. Giancoli, zm. 2006. Fizyka: zasady z aplikacjami. 6th ... Ed Prentice Hall.
4. Hewitt, Paul. 2012. Konceptualna nauka fizyczna. 5. Wyd. osoba.
5. Resnick, r. (1999). Fizyczny. Tom. 1. Wydanie trzecie. po hiszpańsku. Continental Editorial Company S.DO. c.V.
6. Rex, a. 2011. Podstawy fizyki. osoba.
7. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
8. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.