Określenie równowagi translacyjnej, zastosowania, przykłady

On Równowaga translacyjna Jest to stan, w którym znajduje się obiekt jako całość, gdy wszystkie działające na nim siły są kompensowane. Matematycznie jest to równoważne powiedzenie, że F₁+ F₂ +  F₃ +.. . = 0, będąc f₁, F₂,  F₃... zaangażowane siły.

Fakt, że ciało jest w równowadze translacyjnej, nie oznacza, że ​​koniecznie jest w spoczynku. Jest to szczególny przypadek poprzedniej definicji. Obiekt może być w ruchu, ale przy braku przyspieszenia będzie to jednolity ruch prostoliniowy.

Rysunek 1. Równowaga tłumaczeń jest ważna dla dużej liczby sportów. Źródło: Pixabay.

Więc jeśli ciało jest w spoczynku. A jeśli już masz ruch, będzie miał stałą prędkość. Zasadniczo ruch dowolnego obiektu jest składem tłumaczeń i obrotów. Tłumaczenia mogą być pokazane na rysunku 2: liniowe lub krzywoliniowe.

Ale jeśli jeden z punktów obiektu jest ustalony, to jedyną możliwością poruszania się jest obrócenie. Przykładem tego jest CD, którego centrum jest ustalone. CD ma możliwość obracania się wokół osi, która przechodzi przez ten punkt, ale nie poruszać się.

Gdy obiekty mają stałe punkty lub są obsługiwane na powierzchniach, mówi się o spinki do mankietów. Linki oddziałują na ograniczenie ruchów, które obiekt jest w stanie wykonać.

[TOC]

Określenie równowagi translacyjnej

Dla cząstki w równowadze należy upewnić się, że:

F_R = 0

Lub w notacji podsumowującej:

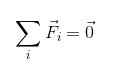
Oczywiste jest, że aby ciało było w równowadze translacyjnej, siły, które działają na nią, muszą być w jakiś sposób zrekompensowane, aby jego wynik był nieważny.

W ten sposób obiekt nie doświadczy przyspieszenia, a wszystkie jego cząsteczki są w spoczynku lub eksperymentalne tłumaczenia prostoliniowe ze stałą prędkością.

Może ci służyć: teoria Wielkiego Wybuchu: cechy, etapy, dowody, problemy

Teraz, jeśli obiekty mogą się obrócić, na ogół to zrobią. Dlatego większość ruchów składa się z kombinacji translacji i rotacji.

Rotacja obiektu

Gdy bilans obrotowy jest ważny, może być konieczne upewnienie się, że obiekt się nie obraca. Następnie musisz przestudiować, czy działają na to momenty, czy momenty.

Moment obrotowy jest wielkością wektora, na której zależą obroty. Wymaga zastosowania siły, ale ważny jest również punkt tego zastosowania. Aby wyjaśnić pomysł, rozważ rozszerzony obiekt, na którym działa siła F I zobaczmy, czy jesteś w stanie wytworzyć obrót w odniesieniu do jakiejś osi, czy.

Jest już intuiowane, że popychając obiekt w punkcie P siłą F, Możliwe jest odwrócenie punktu o, w kierunku antyhorarycznym. Ale kierunek, w którym stosuje się siłę, jest również ważny. Na przykład siła przyłożona na rysunku medium nie będzie w stanie obrócić obiektu, chociaż z pewnością może go poruszyć.

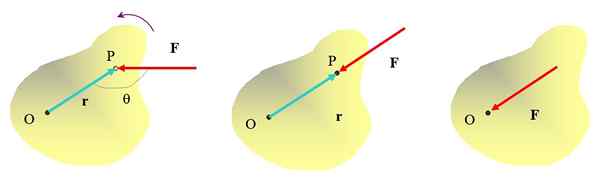Rysunek 2. Różne sposoby zastosowania siły na rozległy obiekt, tylko na rysunku skrajnego lewicy uzyskuje się efekt obrotu. Źródło: Self Made.

Zastosuj siłę bezpośrednio w punkcie lub nie będzie używana do obrócenia obiektu. Wtedy jasne jest, że aby osiągnąć efekt obrotu, siła należy nałożyć w pewnej odległości od osi obrotu, a jej linia działania nie powinna przechodzić przez tę oś osi.

Definicja momentu obrotowego

Moment obrotowy lub moment siły, oznaczony jako τ wielkość wektora odpowiedzialna za złożenie wszystkich tych faktów, jest zdefiniowana jako:

τ = r x f

Wektor R Jest skierowany od osi obrotu do punktu zastosowania siły, a udział kąta między R i F jest ważny. Dlatego wielkość momentu obrotowego wyraża się jako:

Może ci służyć: pierwsze prawo Newtona: formuły, eksperymenty i ćwiczenia

τ = r.F.Sen Q

Najbardziej skuteczny moment obrotowy ma miejsce, gdy R I F Są prostopadłe.

Teraz, jeśli pożądane jest, aby nie było obrotu lub przechodzące te przy stałym przyspieszeniu kątowym, konieczne jest, aby suma momentów obrotowych działających na obiekcie była zerowa, analogiczna do tego, co uwzględniono dla sił:

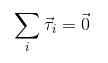
Warunki równowagi

Bilans oznacza stabilność, harmonię i równowagę. Aby przepływ obiektu ma te cechy, należy zastosować warunki opisane w poprzednich sekcjach:

1) f₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

Pierwszy warunek gwarantuje równowagę translacyjną, a drugie rotacyjne. Oba muszą zostać spełnione, jeśli obiekt ma być w stanie pozostać równowaga statyczna (brak ruchu).

Aplikacje

Warunki równowagi mają zastosowanie do wielu struktur, ponieważ gdy budowanie budynków lub różnorodnych obiektów jest wykonane z zamiarem utrzymywania ich w tych samych względnych pozycjach. Innymi słowy, że obiekt nie jest rozbrojony.

Jest to ważne na przykład przy budowaniu mostów, które pozostają twarde pod ich stopami lub przy projektowaniu struktur zamieszkania, które nie zmieniają pozycji lub mają tendencję do zrzucania.

Chociaż uważa się, że jednolity ruch prostoliniowy jest skrajnym uproszczeniem ruchu, który zwykle występuje niewiele z natury, należy pamiętać, że prędkość światła w pustce jest stała, a dźwięk również w powietrzu, jeśli, jeśli, jeśli, jeśli, jeśli też dźwięk w powietrzu rozważa jednorodne dla środowiska.

W wielu strukturach mobilnych wykonanych przez człowieka ważne jest, aby zachować stałą prędkość: na przykład na schodach mechanicznych i liniach montażowych.

Może ci służyć: drugie prawo termodynamiki: wzory, równania, przykłady

Przykłady równowagi translacyjnej

To jest klasyczne ćwiczenie napięć, które utrzymują lampę w równowadze. Wiadomo, że lampa waży 15 kg. Znajdź wielkości niezbędnych napięć, aby utrzymać je w tej pozycji.

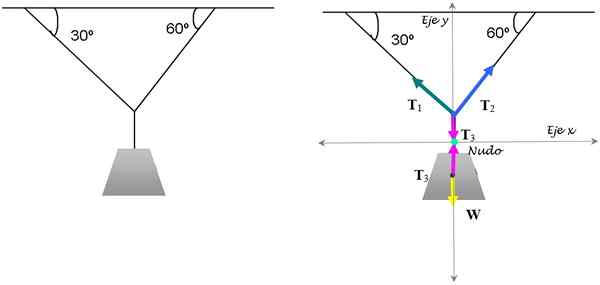Rysunek 3. Równowaga lampy jest gwarantowana poprzez zastosowanie warunków równowagi translacyjnej. Źródło: Self Made.

Rozwiązanie

Aby go rozwiązać. Odpowiednie schematy wolnego ciała dla węzła i lampy pokazano na powyższym rysunku.

Waga lampy jest W = 5 kg . 9.8 m/s² = 49 n. Aby lampa była w równowadze, wystarczy, aby pierwszy warunek równowagi został spełniony:

T₃ - W = 0

T₃ = W = 49 n.

Napięcia T₁ I T₂ Muszą się rozłożyć:

T_1Y + T_{2 i} - T₃ = 0 (Lato sił wzdłuż osi y))

-T_1x +T_2x = 0 (Lato sił wzdłuż osi x)

Zastosowanie trygonometrii:

T₁.Cos 60º +t₂ .Cos 30º = 49

- T₁.Sen60º +t₂.Sen30º = 0

Jest to system dwóch równań z dwoma niewiadomymi, których odpowiedź brzmi: T₁ = 24.5 n I T₂ = 42.4 n.

Bibliografia

1. Rex, a. 2011. Podstawy fizyki. osoba. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7^mama. Wyd. Cengage Learning. 120 - 124.
3. Serway, r., Vulle, c. 2011. Podstawy fizyki. 9^na Wyd. Cengage Learning. 99-112.
4. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fizyka. Addison Wesley. 332 -346.