Warunki równowagi tłumaczeń, przykłady, ćwiczenia

Stwierdzono, że obiekt jest w środku Równowaga tłumaczenia Kiedy suma sił, które na nim działają, wynosi zero. Nie oznacza to, że koniecznie jest reszta, ale ruch, jeśli istnieje, byłby jednolity lub wyłącznie obrotowy prostoliniowy, w przypadku bycia rozległym obiektem.

Warunki równowagi mechanicznej oparte są na przepisach dotyczących mechaniki Newtona. Rzeczywiście, pierwsze prawo mówi nam, że obiekt jest w spoczynku lub porusza się z jednolitym ruchem prostoliniowym MRU, pod warunkiem, że nie działa na niego siły netto.

Ten lamppost jest w równowadze tłumaczeń

Teraz wynikowa siła lub siła netto jest po prostu sumą wektorową wszystkich sił działających na obiekt. Zgodnie z drugim prawem Newtona suma ta musi być równa produktowi między masą a przyspieszeniem, ale jeśli obiekt nie jest przyspieszony, suma ta jest unieważniona.

A ponieważ nie ma przyspieszenia, wspomniane dwie możliwości: ciało jest w spoczynku, to znaczy nie porusza się, a jeśli tak, musi to być z MRU. W pierwszym przypadku mówi się o statycznej równowagi ponadnarodowej, aw drugiej dynamice.

Równowaga tłumaczenia jest ważnym czynnikiem w wielu aspektach inżynierii, na przykład w budownictwie. Elementy tworzące budynek: wiązki, kable, ramki i inne, muszą być w równowadze, aby zagwarantować stabilność obudowy.

Równowaga tłumaczenia jest również poszukiwana w strukturach mobilnych, takich jak schody mechaniczne, pasma transportowe i w praktyce licznych sportów.

[TOC]

Warunek równowagi tłumaczenia

Załóżmy, że kilka sił działa na ciało, które oznaczamy jako F₁, F₂, F₃.. . F_N, używając odważnej litery, aby podkreślić fakt, że siły są wektorami i należy je dodać jako takie.

Wektorowa suma wszystkich tych sił jest nazywana wynikowa siła albo Siła wypadkowa. Jeśli to podsumowanie powoduje wektor zerowy, warunek bilansu tłumaczenia jest spełniony:

Może ci służyć: zamknięty obwód elektryczny

F₁+ F₂+ F₃.. .+ F_N = 0

Ten warunek można zapisać kompaktowo za pomocą podsumowania:

∑ F_Siema = 0

Pod względem składników powstającej siły poprzednie równanie, które jest wektorem, można podzielić na trzy równania skalarne, po jednym dla każdego składnika siły powstałej:

∑ f_IX = 0; ∑ f_I = 0 i ∑ f_z = 0

W praktyce nie jest to łatwe.

Jest to powód, dla którego rzeczywiste obiekty prawie nigdy nie są zwolnione z sił zewnętrznych, a w konsekwencji trudno jest uzyskać równowagę tłumaczenia.

Tak więc inżynierowie używają mechanizmów zmniejszania wcierania, takich jak łożyska i stosowanie olejków smarowych.

Darmowe schematy ciała

Schemat wolnego ciała jest schematem, w którym narysowane są siły działające na ciele. Gdy poszukiwana jest równowaga tłumaczenia, siły te muszą być zrównoważone. Na przykład, jeśli działasz skierowaną siłą pionową, taką jak waga, musi istnieć siła pionowa w górę, która ma dokładnie taką samą wielkość.

Siła ta może być dostarczana przez rękę, która wytrzymuje obiekt, aby nie spada, lina lub po prostu powierzchnia stołu.

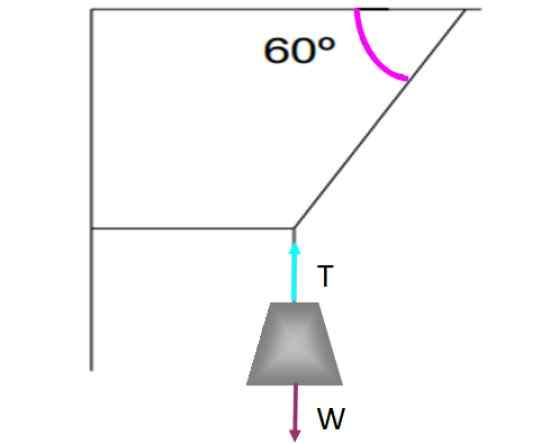
Jeśli na powierzchni istnieje siła styczna, taka jak tarcia kinetyczne lub statyczne, musi istnieć inna przeciwna siła, aby istniała równowaga. Na przykład obserwujmy ciężar zwisający z ciągów pokazanych na poniższym rysunku.

Przykład obiektu, który jest w równowadze tłumaczenia, to waży podleganie dachu za pomocą ciągów ułożonych jak pokazano na obrazie. Źródło: f. Zapata.

Waga pozostaje w równowadze tłumaczenia i bez poruszania T To kompensuje wagę W. Każda siła była reprezentowana na zachodzie przez strzałę, każda o równym rozmiarze i z tym samym kierunkiem, ale przeciwnym kierunkiem.

Może ci służyć: proces izobaryczny: formuły, równania, eksperymenty, ćwiczenia

Siła równowagi

Załóżmy, że zestaw sił działa na obiekt. To się nazywa System sił z których powstały.

Cóż, siłą przeciwną do tego wyniku jest nazywana Siła równowagi. Jeśli powstała siła jest F_R A siła równowagi jest I, Więc:

I + F_R = 0

Dlatego:

I = - F_R

Przykłady równowagi tłumaczenia

Wiele obiektów, które znajdujemy codziennie, wewnątrz i poza domem, jest w równowadze tłumaczeń:

Budynki i drogi

Budynki i drogi są zbudowane tak, aby pozostać stabilne i nie obracają ani nie zapadają się. Jednak w wieżowcach i ogólnie bardzo wysokich budynkach konieczna jest pewna elastyczność, aby oprzeć się działaniu wiatru.

Książki i przedmioty na półkach

Książki w bibliotece i produkty w sklepach to obiekty, które pozostają w równowadze tłumaczeń i bez ruchu.

Meble

Meble, telewizor z płaskim ekranem i obrazy na ścianie, a także lampy zwisające z sufitu, aby wymienić niektóre obiekty, są w równowadze tłumaczenia.

Światła uliczne

Światła światła są przymocowane przez słupki i kable, aby nie upadły. Wiemy jednak, że wiatr sprawia, że ​​oscylują.

Oświetlenie publiczne

Publiczne światła oświetlenia są również w równowadze tłumaczeń, ustalone na postach światła, takie jak główny obraz głównego obrazu.

Ćwiczenie rozwiązane

Jaka wielkość powinna mieć siła F_S Tarcie statyczne, aby pudełko na rysunku pozostać w spoczynku na środku pochyłej płaszczyzny, kąt α 37º? Masa pudełka wynosi m = 8 kg.

Może ci służyć: API Gravity: Skala i klasyfikacja ropy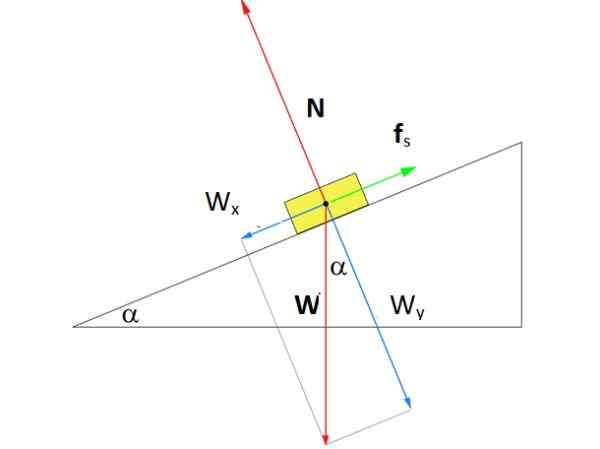Schemat wolnego ciała dla obiektu odpoczynku na pochylonej płaszczyźnie. Źródło: f. Zapata.

Rozwiązanie

Rysunek pokazuje schemat wolnego ciała na płaszczyźnie. Działają na nią trzy siły: waga W, skierowane pionowo, normalne N, która jest siłą prostopadłą wywieraną przez powierzchnię płaszczyzny nad pudełkiem, a wreszcie siła tarcia statyczna F_S To sprzeciwia się pudełku, aby zsunąć się w dół.

Warunek równowagi tłumaczenia określa, że:

W + N + F_S = 0

Ale musisz pamiętać, że jest to suma wektorowa i aby ją wykonać, konieczne jest rozkład sił na komponenty wzdłuż osi współrzędnych.

Na rysunku narysowano układ współrzędnych, w którym oś x biegnie równolegle do powierzchni nachylonej płaszczyzny. Z tym wyborem tarcie statyczne spada na tę oś, podczas gdy normalna jest na osi i. Waga jest jedyną siłą, która jest pochylona i musimy rozłożyć za pomocą trygonometrii:

W_X = W. sin α
W_I = W. cos α

Suma sił w każdej osi to:

∑ f_I = N - w_I = 0
∑ f_X = f_S - W_X = 0

Z tego ostatniego równania wynika, że:

F_S = W_X

I jak w_X = W. sin α i wielkość wagi z kolei wynosi w = m.g, będąc garzem grawitacji, więc wielkość statycznego dotyku jest po prostu:

F_S = M⋅G⋅Sen α = 8 kg × 9.8 m/s² × Sen 37º = 47.2 n.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Głośność 2. Dynamiczny. Pod redakcją Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
4. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7^mama. Wyd. Cengage Learning.
5. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. McGraw Hill.