Równania ułamkowe
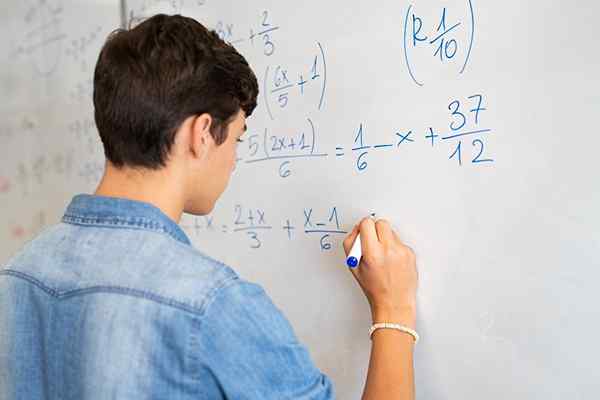
- 880
- 244
- Estera Wojtkowiak
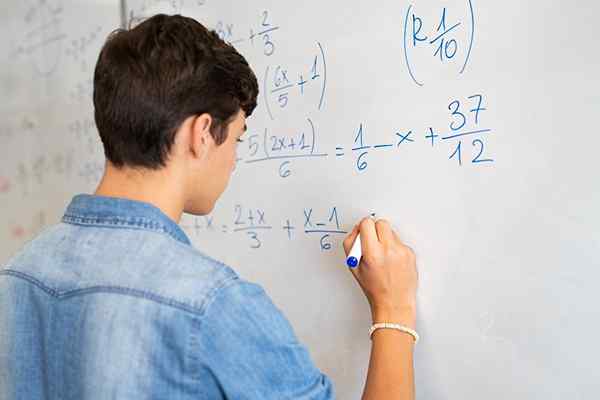 Równania ułamkowe obejmują frakcje numeryczne i/lub algebraiczne, a nieznane mogą być zarówno w licznikach, jak i mianowniku, lub obu
Równania ułamkowe obejmują frakcje numeryczne i/lub algebraiczne, a nieznane mogą być zarówno w licznikach, jak i mianowniku, lub obu Jakie są równania ułamkowe?
równania ułamkowe Czy te, które zawierają ułamki w jednym lub większej liczbie swoich terminów. Takie frakcje mogą być numeryczne lub algebraiczne, gdzie nieznane można znaleźć w liczniku i/lub w mianowniku dowolnego terminu.
Następnie niektóre przykłady równań ułamkowych z jednym nieznanym:
Pierwszym przykładem jest równanie liniowe z współczynnikami ułamkowymi; W drugim przykładzie nieznane jest mianownik każdego z terminów, aw ostatnim nieznany jest zarówno licznik.
Aby je rozwiązać, konieczne jest przeprowadzenie niektórych transformacji algebraicznych, a tym samym uzyskania równania równoważnego, w którym nieznany nie pojawia się w mianowniku. Po przeprowadzeniu tej procedury rozwiązanie zostanie znalezione przy użyciu odpowiednich technik.
Rozwiązanie składa się z zestawu wartości „x”, które spełniają równość. Może to być unikalna wartość lub kilka, ale w każdym razie bardzo ważne jest, aby pamiętać, że nie wszystkie rozwiązania w równaniu równoważnym są dopuszczalne dla pierwotnego równania.
Rzeczywiście, jeśli jest to równanie, którego nieznane jest mianownik, wartości „x”, których należy unikać, nawet jeśli należą one do zestawu równoważnych rozwiązań równań. Wynika to z faktu, że podział między 0 nie jest zdefiniowany.
Jeśli równanie równoważne ma unikalne rozwiązanie i okazuje się, że mianownik dowolnego z warunków oryginalnego równania jest anulowany, to nie ma rozwiązania.
Jak rozwiązać równanie ułamkowe
Operacje przeprowadzane w celu rozwiązania równań niefrakcyjnych są prawidłowe, pod warunkiem, że równość jest utrzymywana. W ten sposób w równaniu ułamkowym można dodać lub odjąć tę samą ilość do obu stron równości, pomnożyć wszystkie terminy przez tę samą kwotę lub podzielić każdy termin przez tę samą kwotę (inną od 0).
Może ci służyć: twierdzenie BolzanoAle ponieważ równanie ułamkowe jest konieczne do przekształcenia w inny odpowiednik bez mianowników, przestrzegane są również następujące ogólne wskazania:
- Znajdź minimalną wspólną wielokrotność mianowników (m.C.M).
- Pomnóż każdy termin przez m.C.M., W celu wyeliminowania mianowników.
- Rozwiąż uzyskane równanie równoważne.
- Sprawdź, czy znalezione rozwiązania spełniają pierwotną równość.
Rodzaje równań równoważnych
Równania równoważne uzyskane po wskazanej procedurze mogą wynosić:
- Liniowy lub pierwszy stopień
- Kwadratowy
- Wyższego rzędu
Rozwiązane przykłady
Przykład 1
Rozwiąż następujące równanie:
Należy zauważyć, że równanie jest pierwszym stopniem w „x”, ponieważ „x” jest wysoki w 1. Współczynniki równania są ułamkami i sposobem ich wyeliminowania, pracy z liczbami całkowitymi, mnożą wszystkie terminy przez minimalną wielokrotność mianowników (m.C.M.).
M.C.M. (2,3,6) = 6
Więc:
3x - 2x = 1
x = 1
Czytnik może sprawdzić ważność tego rozwiązania, zastępując x = 1 w oryginalnym równaniu i sprawdzić, czy uzyskuje się równość.
Przykład 2
Określ wartości „x”, które spełniają:
W przeciwieństwie do poprzedniego przykładu, w tym przypadku nieznane jest w mianowniku. Zauważ, że mianowniki są unieważnione dla wartości x = 2 i x = −1, detal, który jest wygodny do uwzględnienia, ponieważ jeśli równanie równoważne przyznaje te rozwiązania, musimy je odrzucić, ponieważ nie są one dopuszczalne w oryginalnym równaniu.
Teraz musimy przekształcić równanie w inne bez mianowników, pierwszym krokiem jest uczynienie sumę terminów po lewej stronie równości:
Ponieważ mianowniki są takie same, więc równość jest spełniona, konieczne jest również, aby liczniki również były:
Może ci służyć: proporcjonalność stała: co to jest, obliczenia, ćwiczenia4 (x+1) - 3 (x -2) = 8
Wystarczy rozwiązać to równanie, które okazuje się być pierwszą klasą:
4x + 4 - 3x + 6 = 8
x = 8 - 6 - 4 = - 2
x = - 2
Ponieważ wartość ta różni się od wartości zakazanych, jest przyjmowana jako rozwiązanie pierwotnego równania.
Przykład 3
Znajdź rozwiązanie:
W tym równaniu wartość x = 4 anuluje mianowniki, zatem jest wykluczona z zestawu rozwiązania transformowanego równania, jeśli się wydawało.
Transformowane równanie jest łatwe do znalezienia, wystarczy pomnożyć wszystkie terminy przez współczynnik (x-4):
Przebywający:
2x - 4 = 4
2x = 8
x = 4
Przykład 4
Rozwiązać równanie:
W takim przypadku mianowniki mają kwadratowe terminy, więc wygodne jest je najpierw uwzględnić:
- X2 + 8x + 7 = (x + 7) (x + 1)
- X2 - 49 = (x + 7) (x - 7)
- X2 - 6x - 7 = (x - 7) (x + 1)
Równanie jest takie:
Wartości x, które anulują dowolny z mianowników to: x = −7, x = 7, x = −1. Dlatego nawet jeśli wartości te są częścią zestawu rozwiązań zmodyfikowanego równania, nie mogą być rozwiązaniem pierwotnego równania.
Teraz pojawia się proces transformacji równania. Pierwszym krokiem jest znalezienie minimalnej wspólnej wielokrotności mianowników:
M.C.M. = (x + 7) (x - 7) (x + 1)
Mnożąc po obu stronach równości przez m.C.M. zostaje:
Wynikły:
(x --7) (x− 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)
Za pośrednictwem nieruchomości dystrybucyjnej produkty są opracowywane:
X2 - 9x +14 = 2x2 - 3x - 5 - (x2 + 5x - 14)
Zmniejszenie podobnych warunków po prawej stronie:
X2 - 9x + 14 = x2 - 8x + 9
Kwadratowe warunki są anulowane, spełniając ten sam znak po różnych stronach równości:
Może ci służyć: Kubki Różnica: wzory, równania, przykłady, ćwiczenia- 9x + 14 = - 8x + 9
-x = -5 ⇒ x = 5
Wynik ten jest uznawany za rozwiązanie, ponieważ nie jest to żadna z wartości zabronionych.
Zastosowanie wykonywania równań ułamkowych
Mianownik frakcji przekracza cztery jednostki do licznika. Jeśli licznik jest odejmowany od licznika i mianownika, wynikowy ułamek wynosi 3/5. Określ pierwotną frakcję.
Rozwiązanie
Niech x będzie wartością licznika.
Ponieważ mianownik frakcji przekracza cztery jednostki do licznika, pierwotna frakcja to:
Teraz musisz odjąć 5 jednostek, zarówno do licznika, jak i mianownika:
Ponieważ ułamek wynikający z przeprowadzenia poprzedniej procedury jest równy 3/5, są one wyrównane:
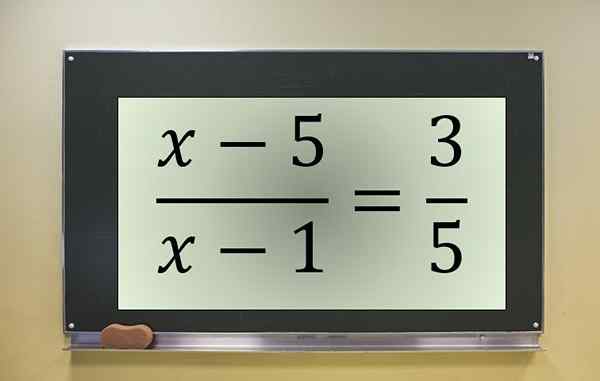 Przykład równania ułamkowego. Źródło: f. Zapata.
Przykład równania ułamkowego. Źródło: f. Zapata. Jest to równanie ułamkowe z nieznanym w liczniku i mianowniku, które jest anulowane przy x = 1. Dlatego wartość tę należy wykluczyć, jeśli należą do rozwiązań transformowanego równania.
Następnie mnoży obie strony przez minimalną wspólną wielokrotność, która wynosi 5 (x - 1):
Powodując następujące równanie równoważne:
5 (x - 5) = 3 (x - 1)
Stosowanie nieruchomości dystrybucyjnej:
5x -25 = 3x - 3 ⇒ 2x = 22
x = 11
Oryginalna frakcja zastępuje x = 11 w wyrażeniu:
W wyniku czego ułamek 11/15. To jest odpowiedź na podniesiony problem.
Bibliografia
- Równania ułamkowe. Odzyskane z: MatemePower.com
- Portal matematyki. Równania ułamkowe. Rozwiązanie problemu. Odzyskane z: Silvioduarte.com.
- Stewart, J. (2007). Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
- Sullivan, m. (1997). Przedłużanie. 4. Wydanie. Edukacja Pearsona.
- Zill, d. (2008). Prefrecment z postępami obliczeniowymi. 4. Wydanie. McGraw Hill.



(x+1))

=6\left%20(%20\frac16%20\right%20))
-3(x-2)(x-2)(x+1)=\frac8(x-2)(x+1))
\left%20(%20\fracxx-4%20\right%20)+(x-4)=(x-4)\left%20(%20\frac4x-4%20\right%20))

(x+1)=\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1))
(x-7)(x+1)\left%20[%20\fracx-2(x+7)(x+1)%20\right%20]=(x+7)(x-7)(x+1)\left%20[%20\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1)%20\right%20])



\left%20(%20\fracx-5x-1%20\right%20)=5(x-1)\frac35)