Wzór równań drugiego stopnia, jak je rozwiązać, przykłady, ćwiczenia
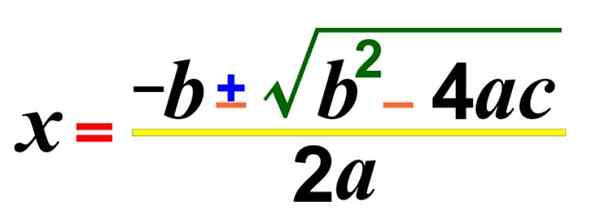
- 703
- 22
- Paweł Malinowski
Równania drugiego stopnia lub kwadratowe I nieznany ma formę topór2 + BX + C = 0. Gdzie A ≠ 0, ponieważ byłby 0, równanie zostanie przekształcone w równanie liniowe, a współczynniki A, B i C są liczbami rzeczywistymi.
Nieznane do ustalenia to wartość x. Na przykład równanie 3x2 - 5x + 2 = 0 jest kompletnym równaniem drugiego stopnia.
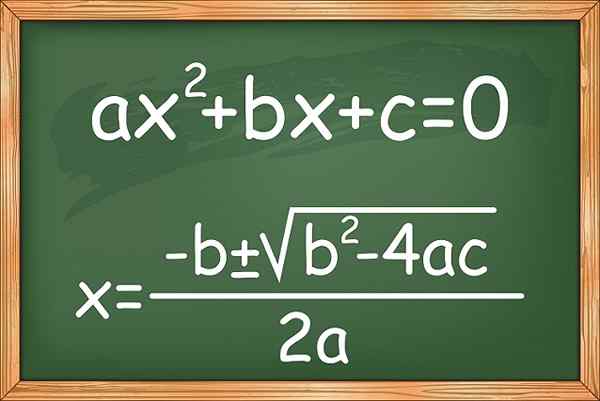 Rysunek 1. Wzór do rozwiązywania równań drugiego stopnia lub kwadratowego nieznanego
Rysunek 1. Wzór do rozwiązywania równań drugiego stopnia lub kwadratowego nieznanego Istnieją również warianty znane jako niekompletne równania drugiego stopnia, które nie mają żadnego z terminów, z wyjątkiem równania topór2. Oto kilka przykładów:
X2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, słynny arabski matematyk starożytności, opisał w swoich pracach Różne rodzaje równań pierwszego i drugiego stopnia, ale tylko z pozytywnymi współczynnikami. Był to jednak francuski matematyka Rozpuszczalnik:
Jest to ogólna formuła, która pozwala rozwiązać równanie kwadratowe, znajdowanie korzeni lub zera tego samego, nawet jeśli roztwory nie są prawdziwe. Istnieją również inne sposoby ich rozwiązania.
[TOC]
Jak rozwiązać równania drugiej klasy?
Drugie równania stopnia można rozwiązać według wzoru podanego powyżej, a także inne procedury algebraiczne, które mogą działać w niektórych równań.
Na początku rozwiążemy proponowane równanie z wzorem, prawidłową metodą dla dowolnego równania drugiego stopnia z niewiadomymi:
3x2 - 5x + 2 = 0
Aby użyć wzoru, poprawnie zauważamy, że:
- Do Jest to współczynnik terminu z x2
- B Jest to współczynnik terminu liniowego
- C jest niezależnym terminem.
Zidentyfikujmy je z tego samego równania:
A = 3
B = -5
C = 2
Zauważ, że znak towarzyszący współczynnikowi należy wziąć pod uwagę. Teraz zastępujemy te wartości w wzorze:
W licznikach jest symbol „mniej - mniej” ±, co wskazuje, że ilość z korzeniem może być uznana za pozytywną, a także negatywną. Równanie drugiego stopnia ma maksymalnie dwa rzeczywiste rozwiązania, a ten symbol uwzględnia to.
Zadzwoń na x1 i x2 Do tych dwóch rozwiązań:
X1 = (5+1) / 6 = 1
X2 = (5-1)/6 = 4/6 = 2/3
Rozdzielczość przez czynnikowanie
Niektóre równania drugiego stopnia składają się z trynomianów, które są łatwe do współczynnika. Jeśli tak, ta metoda jest znacznie szybsza. Rozważ równanie:
X2 + 7x - 18 = 0
Faktoryzacja ma tę formę:
Może ci służyć: zgodność: zgodne dane, kryteria, przykłady, ćwiczenia(x +) ⋅ (x -)
Puste przestrzenie są wypełnione dwiema liczbami, które po mnożonej w 18, a po odjęciu 7 to 7 to 7. Znaki w nawiasach są wybierane z tym kryterium:
-W pierwszym nawiasie umieszczany jest znak między pierwszym a drugim.
-A w drugim nawiasie idzie iloczyn widocznych znaków.
Jeśli chodzi o liczby, są one łatwo w tym przypadku: mają one 9 i 2. Najstarszy jest zawsze umieszczony w pierwszym nawiasie, jak ten:
X2 + 7x - 18 = (x + 9). (x - 2)
Czytelnik może sprawdzić właściwość dystrybucyjną, która podczas opracowywania iloczyn prawej strony równości, uzyskuje się trynomiast lewej. Teraz równanie jest przepisane:
(x + 9) ⋅ (x - 2) = 0
Aby równość mogła się spełnić, wystarczy, aby jeden z dwóch czynników wynosił zero. Więc w pierwszym trzeba to zrobić1 = -9 lub może być to, że drugi czynnik jest anulowany, w takim przypadku x2 = 2. To są rozwiązania równań.
Metoda graficzna
Korzenie lub roztwory równania drugiego stopnia odpowiadają przecięciom przypowieści y = = topór2 + BX + c Z osą poziomą lub osą x. Tak, że wykresując odpowiednią przypowieść, znajdziemy rozwiązanie równania drugiego stopnia, działając y = 0.
Cięcia przypowieści o osi poziomej reprezentują roztwory równania topór2 + BX + C = 0. Przypowieść, która przecina tylko osi poziomą w jednym punkcie, ma pojedynczy korzeń i zawsze będzie wierzchołkiem paraboli.
I wreszcie, jeśli przypowieść nie przecięje osi poziomej, odpowiednie równanie topór2 + BX + C = 0 Brakuje prawdziwych rozwiązań.
Budowanie wykresu ręcznego może być pracochłonne, ale przy użyciu programów, które wykresują online, jest bardzo proste.
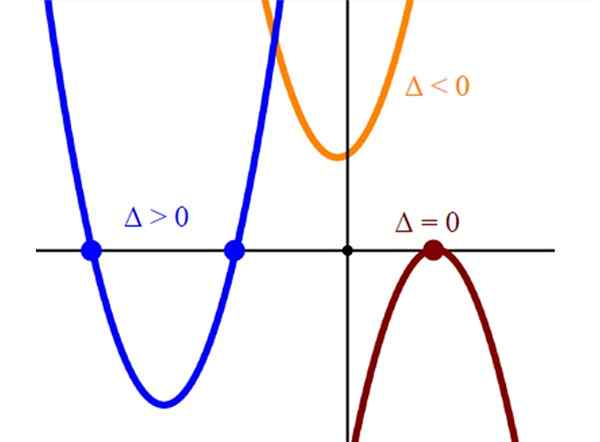 Rysunek 2. Graficzna reprezentacja trzech rodzajów przypowieści, z dwoma, jedną i bez przecięcia z osą poziomą. Źródło: Wikimedia Commons.
Rysunek 2. Graficzna reprezentacja trzech rodzajów przypowieści, z dwoma, jedną i bez przecięcia z osą poziomą. Źródło: Wikimedia Commons. Rozdzielczość za pomocą kalkulatora naukowego
Wiele modeli kalkulatorów naukowych ma możliwość rozwiązania równań drugiego stopnia (a także innych rodzajów równań). Aby to wiedzieć, musisz przejrzeć menu.
Po wybraniu opcji równania kwadratowego nieznanego menu wymaga wprowadzenia wartości współczynników A, B i C i zwrócenia prawdziwych rozwiązań, jeśli istnieją. Istnieją również modele kalkulatorów naukowych, które pracują z liczbami złożonymi i oferują te rozwiązania.
Może ci służyć: wielokrotności 2: co to jest i wyjaśnienieOdróżniający się od równania drugiego stopnia
Aby wiedzieć, czy równanie ma rzeczywiste rozwiązania, czy nie, i ile jest, bez potrzeby rozwiązania, dyskryminant jest zdefiniowany jako kwota pod pierwiastkiem kwadratowym:
Δ = b2 - 4ac
Zgodnie ze znakiem dyskryminacyjnym wiadomo, ile rozwiązań ma równanie zgodnie z tym kryterium:
-Dwa prawdziwe rozwiązania: δ> 0
-Prawdziwe rozwiązanie (lub dwa identyczne rozwiązania): δ = 0
-Brak prawdziwego rozwiązania: δ < 0
Na przykład, ile rozwiązań ma równanie drugiego stopnia ma -7x2 +12x + 64 = 0? Identyfikujemy współczynniki:
A = -7
B = 12
C = 64
Δ = b2 - 4ac = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
Równanie ma dwa rozwiązania. Teraz zobaczmy to:
X2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Jest to równanie z unikalnym rozwiązaniem lub dwoma równymi rozwiązaniami.
Przykłady prostych równań drugiego stopnia
Na początku powiedzieliśmy, że równania drugiego stopnia mogą być kompletne, jeśli trinomial jest i niekompletny, jeśli brakuje terminu lub niezależnego terminu. Teraz zobaczmy niektóre konkretne typy:
X równanie formularzy2 + MX + N = 0
W takim przypadku A = 1, a formuła jest zredukowana do:
W przypadku tego rodzaju równania i zawsze w zależności od pozostałych współczynników, metoda faktoryzacji może działać dobrze, jak widzieliśmy w poprzednim rozdziale.
Niekompletne równanie postaci topora2 + C = 0
Rozwiązaniem, jeśli istnieje, jest forma:
Istnieje prawdziwe rozwiązanie, gdy O C ma znak ujemny, ale jeśli dwa terminy mają ten sam znak, rozwiązanie będzie wyobrażone.
Niekompletne równanie postaci topora2 + Bx = 0
To równanie jest szybko rozwiązywane przy użyciu faktoryzacji, ponieważ x jest wspólnym czynnikiem w obu kategoriach. Jedno z rozwiązań jest zawsze x = 0, druga jest taka:
topór2 + Bx = 0
x (ax + b) = 0
ax + b = 0 → x = -b/a
Spójrzmy wtedy na przykład. Rozwiązywać:
X2 - 5x = 0
x (x - 5) = 0
Dlatego x1 = 0 i x2 = 5
Równania z mianownikiem
Istnieje kilka równań racjonalnych, w których nieznane mogą być obecne zarówno w liczniku, jak i w mianowniku, a nawet tylko w tym ostatnim, a przez manipulacje algebraiczne są redukowane do równań kwadratowych.
Sposobem ich rozwiązania jest pomnożenie obu stron równości przez minimalną wspólną wielokrotność lub m.C.m mianowników, a następnie zmieniają warunki. Na przykład:
Może ci służyć: ile średnich ma obwód?Równania wyższego rzędu, które są przekształcane w kwadratowe
Istnieją równania wyższego rzędu, które poprzez zmienną zmianę można rozwiązać, jakby były kwadratowe, na przykład to równanie Bicadrada:
X4 - 10x2 + 9 = 0
Niech x2 = U, wówczas równanie jest przekształcane w:
Lub2 - 10U + 9 = 0
To równanie jest szybko rozwiązywane przez czynnikowanie, znajdując dwie liczby, które mnożą się w 9 i dodane 10. Te liczby to 9 i 1:
(U - 9).(U - 1) = 0
Dlatego rozwiązania tego równania są u1 = 9 i u2 = 1. Teraz zwracamy zmianę:
X2 = 9 → x1 = 3 i x2 = -3
X2 = 1 → x1 = 1 i x2 = -1
Pierwotne równanie ma kolejność 4, dlatego ma co najmniej 4 korzenie. Przykład to -3, -1, 1 i 3.
Proste rozwiązane ćwiczenia
- Ćwiczenie 1
Rozwiąż następujące równanie kwadratowe z nieznanym w mianowniku:
Minimalna wspólna wielokrotność to x (x+2) i musi pomnożyć na wszystkie terminy:
Równoważne wyrażenie pozostaje:
5x (x+2) - x = x (x+2)
Rozwijamy:
5x2 + 10x - x = x2 + 2x
Wszystkie terminy są transponowane po lewej stronie równości, a po prawej stronie jest po lewej 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
Uwzględniamy, ponieważ jest to niekompletne równanie:
x (4x - 7) = 0
Jednym z rozwiązań jest x = 0, drugi to:
4x = 7
x = 7/4
- Ćwiczenie 2
Znajdź rozwiązanie równań drugiego stopnia:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Rozwiązanie
Z tego równania znamy wyznacznik δ, ponieważ wcześniej obliczono go jako przykład, więc skorzystamy z niego, wyrażając formułę rozpuszczalnika w następujący sposób:
X1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
X2 = (-12-44) / -14 = 4
Rozwiązanie b
Kwadratowy trójmian x2 - 6x + 9 jest możliwe do uwzględnienia, ponieważ jest idealnym kwadratowym trynomikiem:
X2 - 6x + 9 = (x-3)2 = 0
Rozwiązaniem tego równania jest x = 3.
- Ćwiczenie 3
Jakie jest równanie, którego rozwiązania to 3 i 4?
Rozwiązanie
Eresja faktoryzowana jest:
(x - 3) ⋅ (x - 4) = 0
Stosowanie nieruchomości dystrybucyjnej:
X2 - 4x -3x + 12 = 0
Dwa centralne terminy są podobne i można je zmniejszyć, by: opuścić:
X2 - 7x + 12 = 0
Bibliografia
- Baldor. 1977. Algebra podstawowa. Wenezuelskie wydania kulturalne.
- Hoffman, J. Wybór problemów z matematyką. Głośność 2.
- Jiménez, r. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
- Zapata, f. 4 sposoby rozwiązania równania drugiego stopnia. Odzyskane z: Francessphysics.Blogspot.com.
- Zill, d. 1984. Algebra i trygonometria. McGraw Hill.
- « Dodatkowa struktura polimerów, cechy, funkcja, wykorzystanie
- Wewnętrzna charakterystyka motywacji i przykłady »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)