Henderson-Haselbalch Wyjaśnienie, przykłady, ćwiczenia

Równanie Henderson-Haselbalch Jest to wyrażenie matematyczne, które umożliwia obliczenie pH amortyzatora lub roztworu tłumienia. Opiera się na PKA kwasu i związku między koniugatem lub stężeniami soli i kwasu, obecnym w roztworze tłumiącym.

Równanie zostało początkowo opracowane przez Lawrence'a Josepha Hendersona (1878–1942) w 1907 r. Ten chemik ustalił składniki jego równania na podstawie kwasu węglowego jako roztworu buforowego lub bufora.

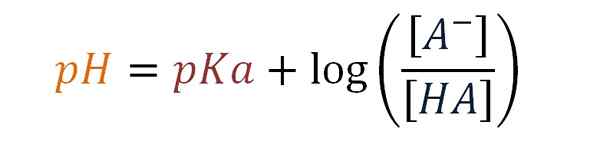Równanie Henderson-Haselbalch. Źródło: Gabriel Bolívar.

Następnie Karl Albert Hasselbalch (1874–1962) wprowadza w 1917 r. Duński chemik badał reakcje krwi z tlenem i wpływ na jego pH.

Roztwór buforowy jest w stanie zminimalizować zmiany pH, które cierpią na roztwór poprzez dodanie silnej objętości kwasu lub zasady. Powstaje przez słaby kwas i jego silna skoniugowana podstawa, która jest szybko zdysocjowana.

[TOC]

Wyjaśnienie

Rozwój matematyczny

Zgodnie z następującym schematem: słaby kwas w roztworze wodnym dysocjuje zgodnie z prawem działania masowego:

Ha +h₂Lub ⇌ h⁺    +     DO^-

HA jest słabym kwasem i^- Twoja skoniugowana baza.

Ta reakcja jest odwracalna i ma stałą równowagi (KA):

Ka = [h⁺] ·[DO^-] / [Ha]

Przyjmowanie logarytmów:

log ka = log [h⁺] +Log [a^-] -log [ha]

Jeśli każdy termin równania jest mnożony przez (-1), jest on wyrażany w następujący sposób:

- log ka = - log [h⁺] -log [a] +log [ha]

- log ka jest zdefiniowany jako pKA i - log [h [h⁺] jest definiowany jako pH. Po dokonaniu należytego podstawienia wyrażenie matematyczne jest zmniejszone do:

pKA = pH -log [a^-] +Log [ha]

Oczyszczając pH i przegrupowanie terminów, równanie wyraża się w następujący sposób:

Może ci służyć: potrójne kowalencyjne link

ph = pka +log [a^-] / [Ha]

To jest równanie Henderson-Haselbalch dla amortyzatora utworzonego przez słabe kwas.

Równanie dla słabej bazy

Podobnie słaba baza może utworzyć roztwór buforowy, a równanie Henderson-Haselbalch jest następujące:

PoH = log PKB +[HB] / [B^-]

Jednak większość roztworów tłumienia pochodzi, w tym roztwory o znaczeniu fizjologicznym, od dysocjacji słabego kwasu. Dlatego najczęściej używanym wyrażeniem dla równania Henderson-Haselbalch jest:

ph = pka +log [a^-] / [Ha]

Jak działa rozwiązanie buforowe?

Akcja amortyzatora

Równanie Hendersona-Haselbalcha wskazuje, że roztwór ten powstaje przez słaby kwas i silną skoniugowaną zasadę wyrażoną jako sól. Ta kompozycja pozwala na utrzymanie roztworu tłumienia ze stabilnym pH, chociaż dodaje się silne kwasy lub zasady.

Dodając silny kwas do amortyzatora, reaguje z sprzężoną podstawą, tworząc sól i wodę. To zneutralizuje kwas i pozwala minimalne zmianę pH.

Teraz, jeśli do amortyzatora dodaje się silna podstawa, reaguje ze słabym kształtem kwasu i wody i soli, neutralizując działanie dodanej podstawy na pH. Dlatego zmienność pH jest minimalna.

PH roztworu buforowego zależy od związku koniugatu stężenia zasady i słabego kwasu, a nie od wartości bezwzględnej stężeń tych składników. Można rozcieńczyć roztwór tłumienia z wodą, a pH praktycznie nie będzie się różnić.

Pojemność amortyzatora

Zdolność tłumienia zależy również od pKA słabego kwasu, a także od stężenia słabego kwasu i podstawy koniugatu. Im bliżej kwasu PKA jest pH roztworem tłumienia, tym większa jego zdolność tłumienia.

Może ci służyć: zasada Le Châtelier

Ponadto, im większe stężenie składników roztworu buforowego, tym większa będzie jego zdolność tłumienia.

Przykłady równań Henderson

Bufor octanu

ph = pka +log [cho₃Gruchać^-] / [Cho₃Cooh]

PKA = 4,75

Kwas węglowy amortyd

ph = pka +log [HCO₃^-] / [H₂WSPÓŁ₃]

PKA = 6.11

Jednak globalny proces, który prowadzi do tworzenia jonów wodorowęglanowych w żywym organizmie, jest następujący:

WSPÓŁ₂   +    H₂Lub ⇌ HCO₃^-   +    H⁺

Bycie co₂ Gaz, jego stężenie w roztworze jest wyrażane zgodnie z jego częściowym ciśnieniem.

ph = pka +log [HCO₃^-] / α · pco₂

α = 0,03 (mmol/l)/mmhg

Pco₂ jest częściową presją CO₂

A wtedy równanie byłoby jako:

ph = pka +log [HCO₃^-] / 0,03 · PCO₂

Absorbnik wstrząsu mlekowego

pH = pKA +log [jon mleczanowy] / [kwas mlekowy]

PKA = 3,86

Fosforan amortyzator

pH = pKA +log [fosforan dibasowy] / [fosforan monobazowy]]]

ph = pka +log [HPO₄^2-] / [H₂PO₄^-]

PKA = 6,8

Oksyhemoglobina

ph = pka +log [HBO₂^-] / [Hhbo₂]

PKA = 6,62

Desoxyhemoglobin

ph = pka +log [hb^-] / HBH

PKA = 8,18

Rozwiązane ćwiczenia

Ćwiczenie 1

Absorbator wstrząsu fosforanowego jest ważny w regulacji pH ciała, ponieważ jego PKA (6,8) jest blisko pH w ciele (7,4). Jaka będzie wartość związku [na₂HPO₄^2-] / [Nah₂PO₄^-] równania Henderson-Haselbalch dla wartości pH = 7,35 i PKA = 6,8?

Reakcja dysocjacji Nah₂PO₄^- Jest:

Nie₂PO₄^-  (kwas) ⇌ nahpo₄^2- (Podstawa) +H⁺

ph = pka +log [na₂HPO₄^2-] / [Nah₂PO₄^-]

Oczyszczając związek [sprzężony / kwasowy] dla roztworu tłumienia fosforanu, mamy:

7.35 - 6,8 = log [na₂HPO₄^2-] / [Nah₂PO₄^-]

0,535 = log [na₂HPO₄^2-] / [Nah₂PO₄^-]

10^0,535 = 10^{log [Na2Hpo4] / [NaH2PO4]}

Może ci służyć: difenyloamina

3.43 = [na₂HPO₄^2-] / [Nah₂PO₄^-]

Ćwiczenie 2

Roztwór buforu octanu ma stężenie kwasu octowego 0,0135 M i stężenie octanu sodu 0,0260 M. Oblicz pH roztworu amortyzatora, wiedząc, że PKA dla amortyzatora octanu wynosi 4,75.

Równowaga dysocjacji kwasu octowego wynosi:

Ch₃Cooh ⇌ ch₃Gruchać^-   +    H⁺

ph = pka +log [cho₃Gruchać^-] / [Cho₃Cooh]

Zastępowanie posiadanych wartości:

[Ch₃Gruchać^-] / [Cho₃COOH] = 0,0260 m / 0,0135 m

[Ch₃Gruchać^-] / [Cho₃Cooh] = 1 884

Log 1,884 = 0,275

pH = 4,75 +0,275

pH = 5,025

Ćwiczenie 3

Absorbnik octanu zawiera 0,1 m kwasu octowego i 0,1 M octanu sodu. Oblicz pH roztworza tłumienia po dodaniu 5 ml 0,05 m przy 10 ml kwasu solnego.

Pierwszym krokiem jest obliczenie końcowego stężenia HCL podczas mieszania z roztworem bufora:

Vi · ci = vf · cf

Cf = vi · (ci / vf)

= 5 ml · (0,05 m / 15 ml)

= 0,017 m

Kwas chlorowodorowy reaguje z octanem sodu, tworząc kwas octowy. Dlatego stężenie octanu sodu zmniejsza się o 0,017 mi, a stężenie kwasu octowego wzrasta o tę samą ilość:

pH = log PKA +(0,1 m - 0,017 m) /(0,1 m +0,017 m)

 pH = pKA +log 0,083 / 0,017

= 4,75 -0,149

= 4601

Bibliografia

1. Whitten, Davis, Peck i Stanley. (2008). Chemia. (8 wyd.). Cengage Learning.
2. Jimenez Vargas i J. Mª Macarulla. (1984). Fizjologiczne fizykochemiczne. 6. edycja. Międzyamerykański redakcja.
3. Wikipedia. (2020). Równanie Henderson-Hasselbalch. Źródło: w:.Wikipedia.org
4. Gurinder Khaira i Alexander Kot. (5 czerwca 2019). Przybliżenie Henderson-Hasselbalch. Chemia librettexts. Odzyskane z: chem.Librettexts.org
5. Helmestine, Anne Marie, pH.D. (29 stycznia 2020). Definicja równania Henderson Hasselbalch. Odzyskane z: Thoughtco.com
6. Redaktorzy Enyclopaedia Britannica. (6 lutego 2020). Lawrence Joseph Henderson. Encyclopædia Britannica. Odzyskane z: Britannica.com