Równanie ciągłości

Wyjaśniamy, jakie jest równanie ciągłości, jego wzór, zastosowania, przykłady i proponujemy ćwiczenia do rozwiązania

Jakie jest równanie ciągłości?

równanie ciągłości, W przypadku płynu nieściśliwego stwierdza, że ​​całkowita masa płynu, który krąży przez rurkę, bez utraty i zysków, pozostaje stała. Innymi słowy, ciasto jest zachowane bez zmian, gdy płyn się porusza.

Nieściśliwy płyn to ten, którego gęstość pozostaje w przybliżeniu stała podczas przepływu. Na przykład woda jest cieczą uważaną za nieściśliwą w warunkach standardowych ciśnienia i temperatury.

Istnieje matematyczny sposób wyrażania zachowania masy, w równaniu ciągłości, podanym przez:

DO₁∙ v₁ = A₂∙ v₂

Gdzie v₁ i v₂ Reprezentują prędkość płynu w dwóch odcinkach rury, a₁ już₂ Są to odpowiednie obszary krzyżowe.

Produkt obszarze krzyżowego według prędkości jest nazywany przepływ A równanie ciągłości oznacza, że ​​w całej rurze przepływ jest stały. Przepływ jest również znany jako wskaźnik przepływu, Jest to rozumiane przez dokładnie obserwowanie poprzedniego wyrażenia, którego wymiary to objętość na jednostkę czasu.

Formuła

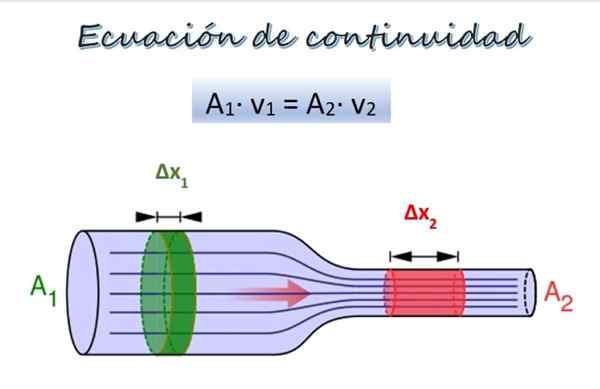
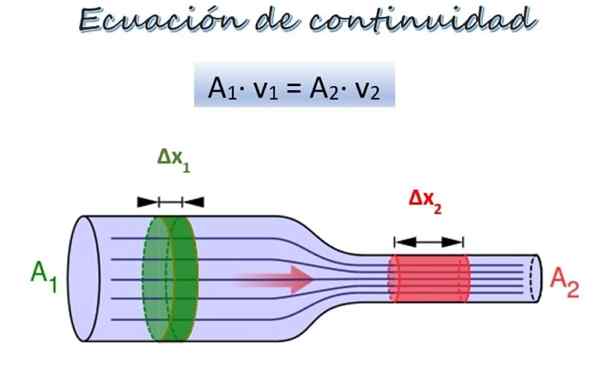Równanie ciągłości przepływu płynu wzdłuż rury o różnych średnicach. Źródło: Wikimedia Commons/F. Zapata.

Na górnym obrazie znajduje się rura o dwóch odcinkach o różnej średnicy i na tej samej wysokości, chociaż mogą znajdować się na różnych wysokościach bez reprezentowania problemu.

W rozdziale 1, szerszym, obszar krzyżowy₁ a płyn porusza się z prędkością v₁, Podczas gdy w rozdziale 2, węższy, jest obszar krzyżowy₂ a prędkość płynu to v₂.

Część ciasta δm₁ (zielony) porusza się według sekcji 1 w czasie δt. W tym okresie część Δm₂ (czerwony) Podróżuj przez sekcję 2. Ponieważ płyn jest nieściśliwy, jego gęstość jest taka sama we wszystkich punktach, więc zaczynając od definicji gęstości:

Może ci służyć: stała Gase: co to jest, obliczenia i przykłady

Tutaj ρ jest gęstością, m to masa i objętość v. Zgodnie z tym masa δm₁ jest równe:

Δm₁ = ρ ∙ v₁

Gdzie tom v₁ Jest to produkt między przekrojem a odległością δx₁:

Δm₁ = ρ ∙ (a₁ ∙ δx₁)

Lecz odkąd:

Następnie część ciasta δm₁ Możesz pisać, pod względem prędkości i czasu ΔT jako:

Δm₁ = ρ ∙ a₁ ∙ δx₁ = ρ ∙ a₁ ∙ (v₁ ∙ δt)

Analogowa część Δm jest pisana₂ To płynie w tym samym czasie do sekcji 2:

Δm₂ = ρ ∙ a₂ ∙ δx₂ = ρ ∙ a₂ ∙ (v₂ ∙ δt)

Przez zachowanie masy:

Δm₁ = Δm₂

I:

ρ ∙ a₁ ∙ v₁ ∙ δT = ρ ∙ a₂ ∙ v₂ ∙ δt

Ponieważ δT i ρ są anulowane, wyniki:

DO₁ ∙ v₁ = A₂ ∙ v₂

Przepływ q

Produkt przekroju A według prędkości płynu V nazywany jest przepływem i oznacza q. Jest to równoważne objętość płynu na jednostkę czasu przez rury lub prędkość przepływu objętościowego:

 V objętość i δt przedział czasu. Szybkość przepływu w międzynarodowym systemie jednostek to m³/s, chociaż stopy sześcienne, galony/min, galony/s litr/s i galony/s są częste. Niektóre z najczęściej stosowanych czynników konwersji są następujące:

• 1 m³/S = 264.172 gal/s
• 1 l/s = 0.001 m³/S
• 1 stóp³/S = 0.0283168 m³/S
• 1 l/s = 0,264172 gal/s
• 1 m³/S = 15850,3 gal/min

Zauważ, że zmniejszając przekrój rurki, prędkość płynu wzrasta i odwrotnie, jeśli przekrój wzrośnie, wówczas prędkość maleje, tak że przepływ jest stały.

Aplikacje i przykłady

Równanie ciągłości stosuje się w analizie przepływu płynu, w połączeniu z równaniem Bernoulli, w którym wzięte są zmiany prędkości płynu w różnych sekcjach, a także zmiany ciśnienia i wpływ wysokości wysokości.

Może ci służyć: prąd stały

Przykład 1

W rodzinnym wężu ogrodowym, gdy woda zwykle opuszcza strumień, ma określony zasięg, ale jeśli położy palec na wyjściu z węża, zmniejszając otwór wyjściowy, zakres strumienia jest większy.

Tutaj równanie ciągłości jest spełnione, ponieważ zmniejszając obszar dyszy wyjściowej, prędkość strumienia wzrasta, tak że powierzchnia prędkości według prędkości jest stała.

Przykład 2

Odrzutowiec zwęża się w miarę upadku, ponieważ jego prędkość wzrasta. W ten sposób prędkość produktu na obszar pozostaje stały

Kolejnym przykładem, w którym wyróżniono równanie ciągłości, jest strumień wodny, który zawęża się, gdy spadnie, ze względu na wzrost prędkości wody podczas upadku.

W ten sposób przepływ jest stały, podczas gdy strumień nadal płynie w reżimie laminarnym, to znaczy woda upada delikatnie bez turbulencji lub wir.

Rozwiązane ćwiczenia

Ćwiczenie 1

Woda krąży za pomocą rury o średnicy 20 cm. Wiedząc, że przepływ wynosi 2000 l/s, znajdź prędkość wody w rurze.

• Rozwiązanie

Wygodne jest wyrażanie wszystkiego w jednostkach systemu międzynarodowego. Po pierwsze, obliczany jest przekrojowy odcinek rury, pamiętając, że promień ma połowę średnicy:

A = π ∙ (d/2)²

D = 20 cm = 0.2 m

Dlatego obszar to:

A = π ∙ (d/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

Przepływ jest wyrażony w m³/s z pomocą odpowiedniego współczynnika konwersji:

Q = 2000 l/s = 2 m³/S

Z wzoru q = a ∙ v prędkość, z jaką płyn krąży przez rurę, jest oczyszczona:

Ćwiczenie 2

Masz zmienną rurę krzyżową, przez którą przepływa woda. W pewnym momencie przekrój to 0.070 m² A prędkość wody wynosi 3.50 m/s. Oblicz:

Może ci służyć: Pascal Zasada: historia, aplikacje, przykłady

a) prędkość wody w innym punkcie rury, której obszar przekroju wynosi 0.105 m².

b) objętość wody, która jest wypisywana przez otwarty koniec w ciągu 1 godziny.

• Rozwiązanie

Stosuje się równanie ciągłości, odpowiadając przepływowi pierwszego punktu do przepływu drugiego. Przepływ to:

Q = a ∙ v

Dla ciągłości:

Q₁ = Q₂

DO₁ ∙ v₁ = A₂ ∙ v₂

Teraz zastępują dane dostarczone przez instrukcję:

• DO₁ = 0.070 m²
• v₁ = 3.50 m/s
• DO₂ = 0.105 m²
• v₂ =?

I oczyszcza v₂:

Rozwiązanie b

Ponieważ przepływ jest również objętością na jednostkę czasu, musi:

Dlatego tom V to:

V = q ∙ δt = (a ∙ v) δt

Przepływ, który można obliczyć na podstawie danych punktu 1 lub z punktu 2, ponieważ jest taki sam w obu punktach:

Q = a₁ ∙ v₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / S

Wiedząc, że 1 godzina = 3600 s, objętość zwolnionej wody wynosi:

V = q ∙ δt = (0.245 m³ / s) × (3600 s) = 882 m³

Za 1 godzinę 882 m są pobierane³ wody przez rury.