Clausius-Clapeyron Równanie Po czym jest przykłady, ćwiczenia
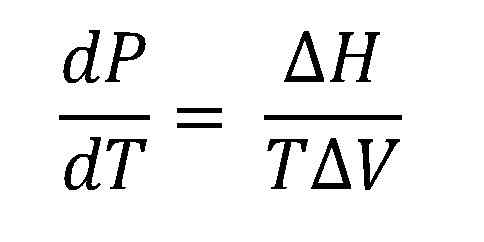
- 2944
- 763
- Arkady Sawicki
Równanie Clausius-Capeyron To taki, który odnosi zmiany ciśnienia pary i temperatury w fazie lub zmianie przejścia stanu. Ma zastosowanie do sublimacji, parowania, fuzji, a nawet zmian w fazach krystalicznych. Warto wspomnieć, że równanie to dotyczy czystej substancji, która jest w równowadze.
Równanie to wywodzi się z praw termodynamicznych i diagramów P-T dla substancji, w której obserwuje się linię współistniejącego; To, co oddziela dwie różne fazy (ciekła, stała ciecz itp.). Aby przenieść tę linię, konieczne jest wzrost lub utrata ciepła, takie jak entalpia para, δhVap.
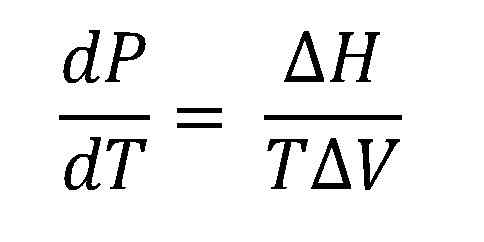 Równanie Clausius-Capeyron. Źródło: Gabriel Bolívar.
Równanie Clausius-Capeyron. Źródło: Gabriel Bolívar. Wyższy obraz pokazuje równanie Clausius-clapeyron przed zintegrowaniem. Zwykle jest to zwykle stosowane do układów ciekłokoporowych, gdzie stosuje się δhVap i chcesz obliczyć, jakie będzie ciśnienie pary ciekłej w określonej temperaturze. Służy również do obliczenia δHVap pewnej cieczy w zakresie temperatur.
Równanie Clausisu-clapeyron jest również stosowane dość często do badania zmian ciśnienia w lotnych stałych; Oznacza to, że rozważana jest entalpia sublimacji, hhpod.
[TOC]
Jakie jest równanie Clausisu-clapeyron?
Obliczanie nacisków i entalpii odparowywania
Z równania Clausiusa-Clapeyrona z góry, w końcu wprowadzono pewne względy matematyczne, aby w końcu wykonać integrację. Na przykład w przypadku układu pręgowanego ciekłego zakłada się, że δhVap Nie różni się w zależności od temperatury i że δv odpowiada wyłącznie objętości pary, gardząc objętością cieczy (vpara-Vpłyn = Vpara).
Zakładając, że para zachowuje się jako idealny gaz i integracja, uzyskuje się równanie zintegrowanego Clausiusa-Clapeyrona:
Może ci służyć: ulatnianie się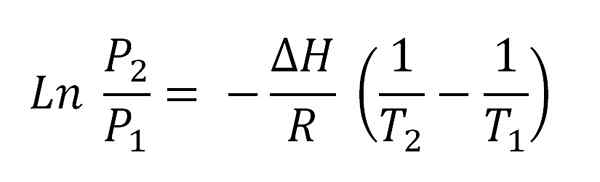 Zintegrowane równanie Clausius-Capeyron.
Zintegrowane równanie Clausius-Capeyron. To równanie odpowiada równomieniu linii graficznej jako:
LN P VS 1/T
I którego ujemnym nachyleniem jest (HH/R). Aby spełnić to równanie, ΔH musi być stałe w przedziale temperatury (t2-T1), w których ciśnienia pary są mierzone w równowadze z cieczy.
W ten sposób, jeśli zakłada się, że ΔH niewiele zmienia się w niewielkich przedziałach temperatury, możliwe jest użycie równania tej linii do przewidywania zmian ciśnienia pary cieczy; A nawet więcej, możesz określić jego δh odparowania.
Im większe są rozważane przedziały temperatury, największe odchylenie tego równania danych eksperymentalnych, i tym mniej zostanie spełnione.
Określenie zmian fazowych
Zatem równanie Clausiusa-Clapeyrona staje się rozwojem linii stycznej do linii współistnień między dwiema fazami fizycznymi, co jest obserwowane na dowolnym schemacie p-t dla substancji.
Jeśli nastąpi zmiana fazowa, nastąpi zmiana na zboczu, a δh nie będzie taka sama. Dlatego, gdy wykazane są silne odchylenia, a równanie się nie powiedzie, jest to znak, że w przedziale temperatury substancja występuje. Oznacza to, że przestaje być systemem pręgowatym, ponieważ jest on przekazywany do linii współistnień odpowiadającej równoważeniu stałego cieczy lub stałego.
Użyj przykładów
- Równanie Clausius-clapeyron zostało wykorzystane w meteorologii do badania zachowania chmur, nawet tych obecnych na innych planetach lub księżycach z atmosferami.
Może ci służyć: kwas glukonowy: struktura, właściwości, synteza, zastosowania- Został zastosowany do określania entalpii fuzyjnej kilku metali, takich jak sód i galu, oraz do ekstrapolacji ich ciśnienia pary w bardzo wysokich temperaturach.
- Zastosowano go również do określenia entalpii odparowywania substancji takich jak chlor gazowy, tetrachlor węglowy, ciekła woda, lód i jod.
- Służył również do badania zmian fazowych w strukturach krystalicznych. W tym ostatnim przykładzie zintegrowane równanie Clausiusa-Clapeyrona wygląda wyjątkowo ina. Zmiany objętości od jednej fazy do drugiej tym razem są małe.
Rozwiązane ćwiczenia
- Ćwiczenie 1
Ciśnienie pary lodowej wynosi 4.58 Torr w 0 ° C i 1.95 Torr A -10 ° C. Jaka jest twoja entalpia sublimacji w tym zakresie temperatur?
Zauważ, że mamy dwa ciśnienia i dwie temperatury:
P1 = 4.58 Torr
P2 = 1.95 Torr
T1 = 0 ° C + 273 = 273 K
T2 = -10 ° C + 273 = 263 K
Konwertujemy jednostki temperaturowe z ° C na k, ponieważ stała R gazów ma K w swoich jednostkach:
R = 8.314 J/k
W ten sposób używamy zintegrowanego równania Clausius-clapeyron i wyraźnego δHpod, który pozostałby jako:
ΔHpod = -Rln (p2/P1) / (1 / t2 - 1 /t1)
Aby uzyskać więcej komfortu, zastąpi tylko liczbami, ale wiedząc, że ostateczną jednostką będzie Joule:
ΔHpod = -(8.314) LN (1.95/4.58)/(1/263 - 1/273)
= 50.97 J
Lub 51.07 J, biorąc pod uwagę kilka dziesiętnych. Ta wartość przedstawi oscylacje w zależności od przedziałów t2-T1 i pewnych presji parowych.
- Ćwiczenie 2
Punktem wrzenia etanolu pod ciśnieniem 760 Torr (1 atm) wynosi 78.3 ° C, a jego entalpia odparowań wynosi 39.3 kJ. Jakie będzie ciśnienie pary w temperaturze 46 ° C?
Może ci służyć: tantalus: struktura, właściwości, użycia, uzyskiwanieIdentyfikujemy dane:
P1 = 760 Torr
P2 = ?
T1 = 78.3 ° C + 273 = 351.3 K
T2 = 46 ° C + 273 = 319 K
ΔHVap = 39.3 kJ lub 39300 J
Więc musimy oczyścić P2 zintegrowanego równania Clausius-Capeyron. Ponownie jednostki zostaną pominięte dla komfortu, a obliczenia zostaną opracowane krok po kroku:
LN (str2/P1) = -(δHVap/R) (1/t2 - 1/t1)
LN (str2/760) = -(39300/8.314) (1/319 - 1/351.3)
LN (str2/760) = -1.36
Zastosowanie funkcji wykładniczej po obu stronach równania, aby móc wyczyścić p2 będziemy mieli:
E (ln p2/760) = e(-1.36)
P2/760 = 0.256
P2 = 0.256 (760)
= 195 Torr
W niższej temperaturze (46 ° C), niższe ciśnienie pary (195 Torr). W rzeczywistości presja etanolu od 760 Torr do 78.3 ° C, mówimy o jego normalnej temperaturze wrzenia. To jest zachowanie oczekiwane dla wszystkich płynów
Ogólnie rzecz biorąc, Ćwiczenia Clausiusa-Capeyron tego typu składają się z wyczyszczenia p2, T2 lub δh odparowania lub sublimacji. Obliczenia zmieniają się znacznie, gdy należy również rozważyć δV, zwłaszcza jeśli chodzi o systemy lub równowagę stałego cieczowego.
Bibliografia
- Whitten, Davis, Peck i Stanley. (2008). Chemia. (8 wyd.). Cengage Learning.
- Wikipedia. (2020). Relacja Clausius-Capeyron. Źródło: w:.Wikipedia.org
- San José State University. (S.F.). Równanie Clausius-Clapeyron:
Wyprowadzenie i zastosowanie przenoszone drogą płciową w meteorologii. Odzyskane z: SJSU.Edu - Grupa Bodner. (S.F.). Równanie Clausius-Capeyron. Źródło: chemed.Chem.Purdue.Edu
- Chieh c. & Casulo a. (18 maja 2020). Równanie Clausius-Capeyron. Chemia librettexts. Odzyskane z: chem.Librettexts.org
- Walter J. Moore. (1962). Chemia fizyczna. (Czwarta edycja). Longmans.

