Dział syntetyczny

Wyjaśniamy, czym jest podział syntetyczny, metodę tego, przykłady i ćwiczenia rozwiązane.

Co to jest podział syntetyczny?

Dział syntetyczny Jest to prosty sposób na podzielenie wielomianowego p (x) przez jedną z postaci d (x) = x - c - c. Na przykład wielomian p (x) = (x⁵+3x⁴-7x³+2x²-8x+1) można go reprezentować jako mnożenie dwóch najprostszych wielomianów (x+1) i (x⁴ + 2x³).

Jest to bardzo przydatne narzędzie, ponieważ oprócz umożliwienia nam podziału wielomianów, pozwala również na ocenę wielomianu P (x) w dowolnej liczbie C, co z kolei wskazuje dokładnie, czy liczba ta wynosi zero, czy nie w odniesieniu do wielomian.

Dzięki algorytmowi podziału wiemy, że jeśli mamy dwa wielomianowe (x) d (x) (x) + r (x), gdzie r (x) jest zero lub jest mniejsze niż q (x). Te wielomiany są znane odpowiednio jako iloraz i pozostałość lub odpoczynek.

W sytuacjach, w których wielomian d (x) jest formy x - c, podział syntetyczny daje nam krótki sposób na znalezienie, którzy są q (x) i r (x).

Metoda podziału syntetycznego

Niech p (x) = a_NX^N+Do_N-1X^N-1+… +A₁x+a₀ Wielomian, który chcemy podzielić i d (x) = x-c dzielnik. Aby podzielić metodą podziału syntetycznego, postępujemy w następujący sposób:

1- W pierwszym rzędzie piszemy współczynniki p (x). Jeśli jakakolwiek moc x nie pojawi się, umieszczamy zero jako jego współczynnik.

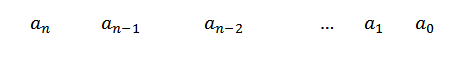
2- W drugim rzędzie, po lewej stronie_N Umieszczamy C i rysujemy linie podziału, jak pokazano na poniższym rysunku:

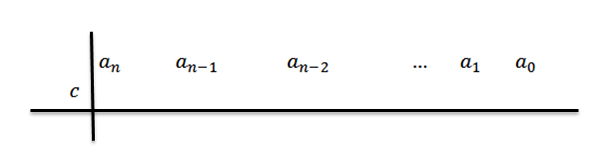
3- Obniamy wiodący współczynnik do trzeciego rzędu.

Może ci służyć: Euler Metoda: jakie jest zastosowanie procedury i ćwiczeń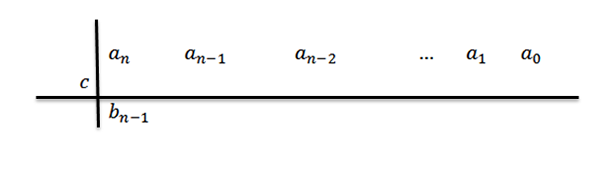

W tym wyrażeniu B_N-1= a_N

4- Rozmnażamy C przez wiodący współczynnik B_N-1 I piszemy wynik w drugim rzędzie, ale kolumna po prawej stronie.

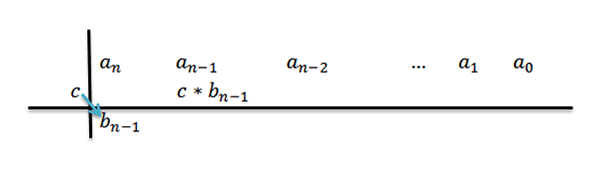
5- Dodajemy kolumnę, w której piszemy poprzedni wynik, a wynik jest umieszczony pod wspomnianą sumą. To znaczy w tej samej kolumnie trzeci rząd.

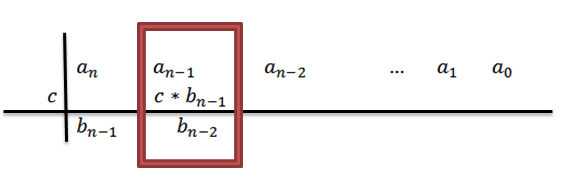
Dodając, mamy w rezultacie_N-1+C*b_N-1, do którego dla komfortu nazwiemy B_N-2

6- Rozmnażamy C przez poprzedni wynik i piszemy wynik po prawej stronie w drugim rzędzie.

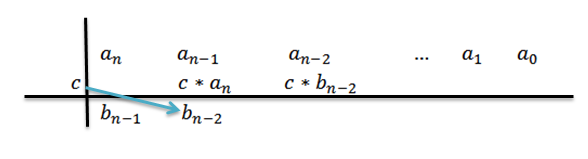
7- Powtarzamy krok 5 i 6, aż osiągniemy współczynnik₀.

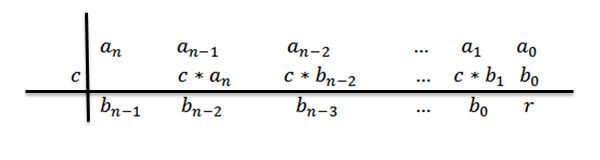
8- Piszemy odpowiedź, to znaczy iloraz i pozostałość. Ponieważ prowadzimy podział wielomianu klasy N między wielomianem klasy 1, mamy iloraz, który byłby klasa N-1.

Współczynniki wielomianu ilorazowego będą liczbą trzeciego rzędu, z wyjątkiem ostatniego, który będzie wielomianem pozostałości lub resztą podziału.

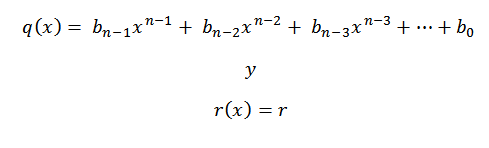
Rozwiązane ćwiczenia

Przykład 1

Stwórz następujący podział metodą podziału syntetycznego:

(X⁵+3x⁴-7x³+2x²-8x+1): (x+1).

Rozwiązanie

Najpierw piszemy współczynniki dywidendy w następujący sposób:

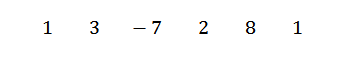
Następnie piszemy C po lewej stronie, w drugim rzędzie, wraz z liniami podziału. W tym przykładzie c = -1.

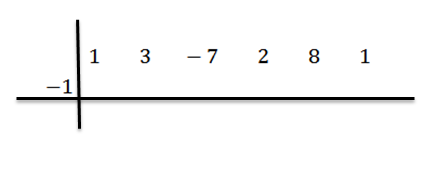
Obniży wiodący współczynnik (w tym przypadku B_N-1 = 1) i mnożymy go przez -1:

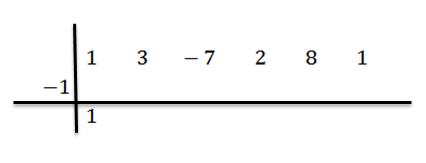
Jego wynik napisaliśmy po prawej w drugim rzędzie, jak pokazano poniżej:

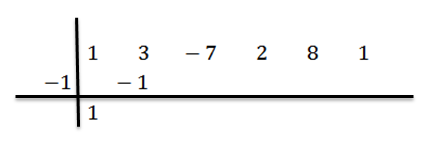
Dodajemy liczby drugiej kolumny:

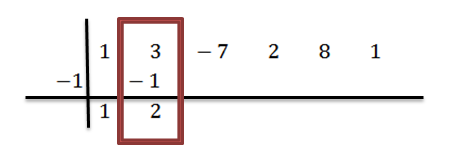
Mnożymy 2 przez -1 i piszemy wynik w trzeciej kolumnie, drugi wiersz:

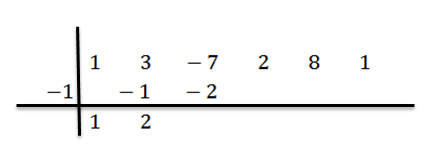
Dodajemy trzecią kolumnę:

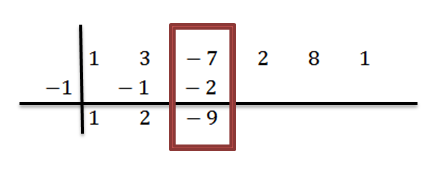
Idą analogicznie, dopóki nie dotrzemy do ostatniej kolumny:

Może ci służyć: domyślne i nadmierne podejście: co to jest i przykłady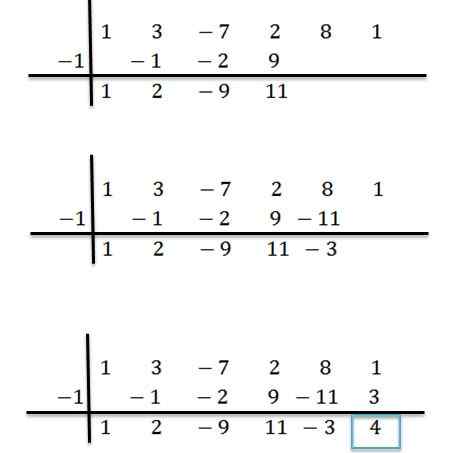

Zatem mamy, że ostatnia liczba uzyskana jest reszta podziału, a pozostałe liczby są współczynnikami wielomianu ilorazowego. Jest to napisane w następujący sposób:

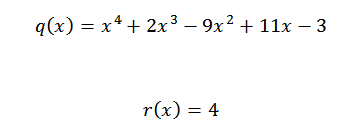
Jeśli chcemy sprawdzić, czy wynik jest poprawny, wystarczy sprawdzić, czy spełnione jest następujące równanie:

P (x) = q (x)*d (x) + r (x)

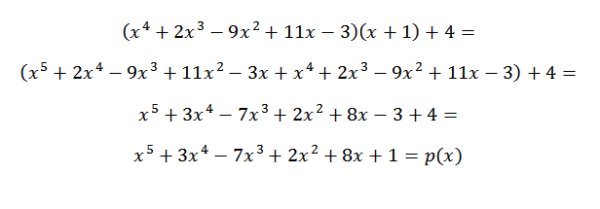
W ten sposób możemy sprawdzić, czy uzyskany wynik jest prawidłowy.

Przykład 2

Wykonaj następujący podział wielomianowy metodą podziału syntetycznego:

(7x³-x+2): (x+2)

Rozwiązanie

W takim przypadku mamy termin x² Nie pojawia się, więc napiszemy do 0 jako jego współczynnik. Zatem wielomian pozostałby jako 7x³+0x²-x+2.

Piszemy twoje współczynniki z rzędu, to znaczy:

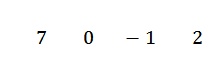
Piszemy wartość C = -2 po lewej stronie w drugim rzędzie i rysujemy linie podziału.

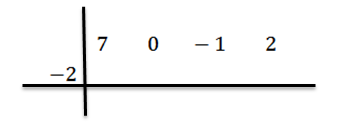
Obniży wiodący współczynnik B_N-1 = 7 i mnożymy go przez -2, pisząc swój wynik w drugim rzędzie po prawej stronie.

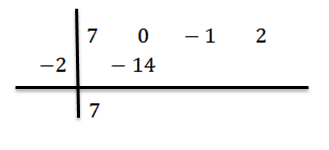
Dodajemy i postępujemy, jak wyjaśniono wcześniej, dopóki nie dotrzemy do ostatniego terminu:

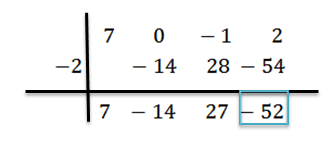
W takim przypadku reszta to r (x) = -52, a otrzymany iloraz jest q (x) = 7x²-14x+27.

Przykład 3

Innym sposobem korzystania z podziału syntetycznego jest następujący.

W przypadku algorytmu podziału możemy napisać wielomian P (x) w następujący sposób:

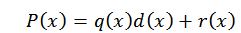
W tym wyrażeniu q (x) i r (x) są odpowiednio ilorazem i resztą. Teraz, jeśli d (x) = x-c, podczas oceny w c w wielomianie znajdujemy następujące:

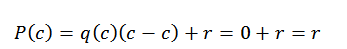
Właśnie dlatego pozostaje tylko znalezienie R (x) i możemy to zrobić dzięki podziałowi syntetycznemu.

Na przykład mamy wielomian p (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x²-37x-37 i chcemy wiedzieć, jaka jest jego wartość podczas oceny przy x = 5. W tym celu przeprowadzamy podział między p (x) i d (x) = x -5 metodą podziału syntetycznego:

Może ci służyć: Symetria osiowa: właściwości, przykłady i ćwiczenia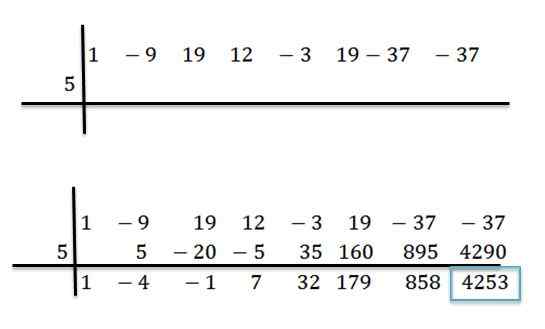

Po zakończeniu operacji wiemy, że możemy napisać p (x) w następujący sposób:

P (x) = (x⁶-4x⁵ -X⁴+ 7x³ +32x² +179x + 858)*(X-5) + 4253

Dlatego podczas oceny musimy:

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(5-5) +4253

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(0) +4253

P (5) = 0 + 4253 = 4253

Jak widzimy, możliwe jest użycie podziału syntetycznego, aby znaleźć wartość wielomianu podczas oceny go w C zamiast po prostu zastępujące C na x. 

Gdybyśmy spróbowali ocenić P (5) w tradycyjny sposób, potrzebowalibyśmy niektórych obliczeń, które zwykle stają się żmudne.

Przykład 4

Algorytm podziału dla wielomianów jest również spełniony dla wielomianów o złożonych współczynnikach, aw konsekwencji mamy, że metoda podziału syntetycznego działa również dla tych wielomianów. Następnie zobaczymy przykład.

Zastosujemy metodę podziału syntetycznego, aby pokazać, że Z = 1+ 2i jest zero wielomianowego p (x) = x³+ (1+i) x² -(1+2i) x+(15+5i). To znaczy pozostałość podziału p (x) między d (x) = x - z jest równa zero.

Postępujemy tak jak poprzednio: W pierwszym rzędzie.

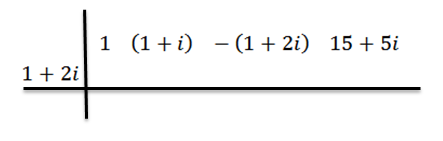
Wydziały robimy jak poprzednio, to znaczy:

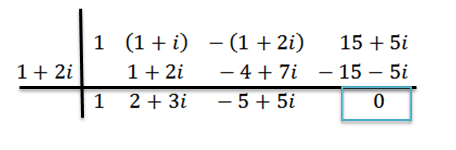
Widzimy, że pozostałość wynosi zero; Dlatego dochodzimy do wniosku, że Z = 1+ 2i ma zero p (x).

Bibliografia

1. Baldor, Aurelio. Algebra. Grupa redakcyjna Patria.
2. Demana, Waits, Foley & Kennedy. Precáculo: graficzny, numeryczny, algebraiczny. Edukacja Pearsona.