Dyskretne rozkłady

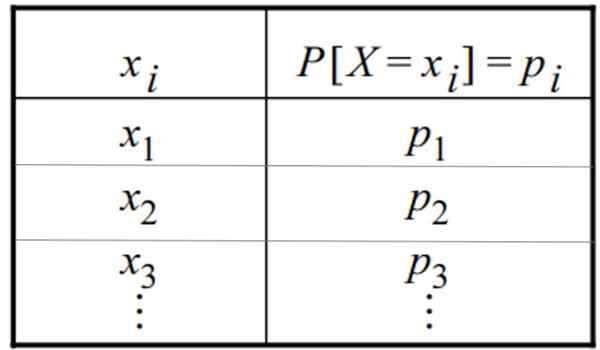Tabela dyskretnego rozkładu prawdopodobieństwa. Źródło: f. Zapata

Co to jest dyskretna dystrybucja?

A dyskretny rozkład prawdopodobieństwa jest funkcją f (x_Siema), która przypisuje każdą wartość zmiennej dyskretnej: x₁, X₂, X₃,... X_Siema, Pewne występowanie wystąpienia p (x = x_Siema). Ta funkcja jest również znana jako „funkcja masy prawdopodobieństwa”.

Dyskretny rozkład prawdopodobieństwa można podać w postaci tabeli lub grafiki. Tabela ma tę ogólną formę, w której zmienna pojawia się w jednej kolumnie, a jej odpowiednie prawdopodobieństwo w drugiej:

Funkcje masy prawdopodobieństwa mają następujące ogólne cechy:

• Prawdopodobieństwo p_Siema każdego wydarzenia x_Siema Jest to od 0 do 1, będąc nawet niektórymi z tych wartości granicznych: 0 ≤ x ≤ 1.
• P (x = x_Siema) = p_Siema Po prostu weź pozytywne wartości: P (x = x_Siema) ≥ 0.
• Prawdą jest, że ∑ p (x_Siema) = 1 dla wszystkich możliwych wartości x.

Rozkład prawdopodobieństwa opisuje zachowanie populacji, opisane przez jej parametry: średnia μ, wariancja σ² i odchylenie standardowe s = σ σ².

Następnie opisano najbardziej znaczące dyskretne rozkłady:

Jednolity rozkład

Jest to najprostszy dyskretny rozkład wszystkich. W nim zmienna może przyjmować wartości dyskretne „n”: x₁, X₂, X₃,... X_Siema, Wszystko z tą samą probabletyzacją. W takim przypadku rozkład jest podany przez:

Rozkład dwumianowy

Dotyczy to tylko dwóch możliwych i wzajemnie wykluczających się wyników, które zwykle nazywane są „sukcesem” i „porażką”, oznaczonymi odpowiednio jako E i F. Fakt, że wydarzenie nazywa się „sukcesem”, niekoniecznie oznacza, że ​​jest to dobra rzecz, jest to raczej arbitralne oznaczenie.

Prawdopodobieństwo sukcesu P (E) w próbach „N” jest oznaczone jako P, a prawdopodobieństwo awarii P (F) jak Q = 1 - P.

Jeśli „x” reprezentuje pewną liczbę sukcesów w niezależnych próbach „N”, prawdą jest, że: 0 ≤ x ≤ n. A prawdopodobieństwo wystąpienia p (x) zdarzenia jest obliczane za pomocą następującego wzoru:

Może ci służyć: centymetry kwadratowe do metrów kwadratowych (CM² do m²)

Gdzie x = 0, 1, 2, 3 ..., n i symbol (!) oznacza „czynnik”:

X! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3)… 1

0! = 1

Dystrybucja Poissona

W tym rozkładowi zmienna losowa x wskazuje, ile razy zdarzenie występuje w pewnym odstępie czasu, co może być czas, odległość lub inne. Występowanie zdarzenia są losowe, niezależne i są równomiernie rozmieszczone w danym przedziale.

Po tych warunkach prawdopodobieństwo, które zależy średnio od μ i liczby eulera lub liczby „E”, oblicza się przez:

Szanse na wydarzenia z tym rozkładem są małe, więc nazywa się to „prawem rzadkich spraw”.

Podejście rozkładu dwumianowego

Rozkład Poissona służy jako podejście do rozmieszczenia dwumianowego, gdy N jest duży (N≥ 100), a P jest mały (NP ≤ 10). W tym przypadku średnia μ jest obliczana jako:

μ = n ∙ p

Rozkład hipergeometryczny

Jest używany, gdy prawdopodobieństwa nie są niezależne, to znaczy po przeprowadzeniu eksperymentu warunki nie są znowu takie same. Tak się dzieje podczas wydobywania próbek bez wymiany z populacji, więc nie można już używać rozkładu dwumianowego.

Jeśli populacja składa się z dwóch rodzajów obiektów odmiennych od i b, a przy losowych obiektach i bez wymiany, prawdopodobieństwo uzyskania x obiektów typu A wynosi:

Gdzie A i B są odpowiednimi ilościami obiektów każdego rodzaju, obecnych w populacji.

Jeśli jednak populacja jest bardzo duża, nawet jeśli nie ma wymiany, trudno jest wybrać ten sam element więcej niż jeden raz, więc oba rozkłady: dwumianowe i hipergeometryczne, dajcie podobne wyniki.

Może ci służyć: Kubki Różnica: wzory, równania, przykłady, ćwiczenia

Przykłady

Monety się uruchamiają

CO -Launches są bardzo ilustracyjnymi przykładami:

-Uruchomienie uczciwej waluty i uzyskaj twarz. Wiadomo, że 1 twarz ma ½ prawdopodobieństwo wyjścia i krzyża (0 twarzy), to samo. Rozkład pokazano w tej tabeli:

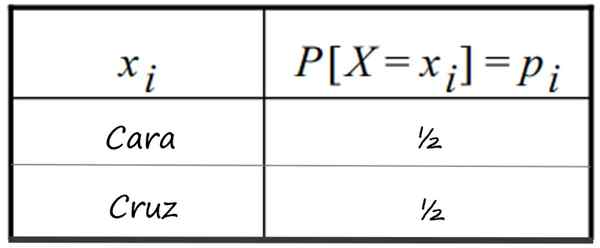Dyskretna tabela rozkładu prawdopodobieństwa, która następuje po uruchomieniu 1 uczciwej waluty. Źródło: f. Zapata

-Jednoczesne ujęcie dwa uczciwe monety i możliwe liczby twarzy, które można uzyskać.

Dyskretna tabela rozkładu prawdopodobieństwa, która następuje po uruchomieniu dwóch uczciwych walut, w celu uzyskania jakiejkolwiek twarzy, czy nie. Źródło: f. Zapata

Zmienne z jednolitym rozkładem

-Wybór liczby całkowitej, która jest równa lub dziwna: każde z nich jest prawdopodobieństwem równym ½ wybranego w zestawie liczb całkowitych.

-Uruchomienie uczciwej kości. W takim przypadku jest 6 numerowanych twarzy i każda z nich ma takie samo prawdopodobieństwo opuszczenia: 1/6.

-Wybór tematu do egzaminu, wybranego spośród N., jeśli wszystkie z nich są równie prawdopodobne.

Zmienne z rozkładem dwumianowym

-Liczba twarzy, które pojawiają się, wprowadzając uczciwą monetę.

-Populacji 250 rodzin, liczba tych, którzy mają 2 dzieci.

-Ilość drzewa różanego, które przetrwają, po ogrodniku 20 Rosales w ogrodzie.

-Z badania z 50 pacjentami liczba z nich, która stanowiła negatywną reakcję na lek.

-Liczba studentów zatwierdzonych na egzamin prawdopodobieństwa grupy złożonej ze 100 studentów.

Zmienne z rozkładem Poissona

-Liczba połączeń na minutę Centrum telefoniczne Firmy.

-Liczba dużych trzęsień ziemi rocznie dla określonego obszaru geograficznego.

-Liczba tornad, które dotknęły określony region w ciągu ostatniego roku.

-Liczba drzew zarażonych grzybem, na kwadratowy hektar lasu.

Zmienne z rozkładem hipergeometrycznym

-Sukcesy liczb lub zwycięskie kombinacje w hazardu.

Może ci służyć: wektory współbieżne: cechy, przykłady i ćwiczenia

-Wybór pewnej liczby kobiet lub mężczyzn w próbce N ryb z rybacki.

Rozwiązane ćwiczenia

Ćwiczenie 1

Badanie wykazało, że przez losowo wybranych dorosłych, którzy mają smartfony, 54% z nich korzysta z nich na zajęciach lub spotkaniach. Chcesz znaleźć prawdopodobieństwo, że losowo wybierając 8 osób ze smartfonem, dokładnie 6 z nich używa ich na zajęciach lub spotkaniach.

Rozwiązanie

Ten eksperyment zgadza się z dwumianowym eksperymentem, ponieważ wynik jest binarny: osoba bierze telefon w klasie lub nie usuwa go. Fakt, że dana osoba używa telefonu w klasie, można nazwać sukcesem, a porażka, jeśli nie jest (zanim wyjaśniono, że ten wybór jest całkowicie arbitralny).

W takim przypadku: p = 0.54 i q = 1- 0.54 = 0.46.

Ponieważ 8 osób jest losowo wybranych, wówczas n = 8, a wartość x wynosi 6, dlatego dostępne są wartości niezbędne, aby zastąpić je w wzorze rozkładu dwumianowego:

Ćwiczenie 2

Przez ostatni rok klinika zarejestrowała 4221 porodów. Za pomocą tych unikalnych danych określ prawdopodobieństwo, że w ciągu 1 dnia odbywa się 15 urodzeń. Czy to wydarzenie jest rzadkie?

Rozwiązanie

Używany jest rozkład Poissona, ponieważ wymaga się określenia prawdopodobieństwa wystąpienia zdarzenia, które występuje w przedziale czasowym. W takim przypadku zmienną jest ilość urodzeń, a przedział wynosi 1 dzień.

Formuła dystrybucji Poissona wymaga średniego urodzeń dziennie, co można łatwo obliczyć:

Dlatego prawdopodobieństwo x = 15 urodzeń/dzień wynosi:

Wynik można wyrazić w kategoriach procentowych klarowności: 6.42% prawdopodobne, że każdego dnia występuje dokładnie 15 porodów. Wydarzenie jest mało prawdopodobne, choć w żadnym wypadku.