Koncepcja odległości euklidianowej, wzór, obliczenia, przykład

Odległość euklidyjska Jest to liczba dodatnia, która wskazuje separację, jaką mają dwa punkty w przestrzeni, w której spełnione są aksjomaty i twierdzenia geometrii euklidów.

Odległość między dwoma punktami a i b przestrzeni euklidowskiej to długość wektora Ab Należący do jedynej linii, która przechodzi przez te punkty.

Rysunek 1 . Jednoznaczna przestrzeń euklidesowa utworzona przez linię (Ox). Pokazano kilka punktów na tej przestrzeni, ich współrzędne i odległości. (Przygotowane przez Ricardo Pérez).

Przestrzeń, którą postrzegamy i tam, gdzie poruszamy istotami ludzkimi, jest przestrzenią trójwymiarową (3-D), w której spełnione są aksjomaty i twierdzenia geometrii euklidów. W tej przestrzeni znajdują się dwa -wymiarowe podprzestrzenie (plany) i jedno wymiarowe (proste) (proste) podprzestrzenia.

Przestrzenie euklidesowe mogą mieć jeden wymiar (1-D), dwie wymiary (2-D), trzy wymiary (3-D) lub N Wymiary (N-D).

Są to punkty w jednej wymiarowej przestrzeni X, które należą do linii zorientowanej (Ox), kierunek od lub do x jest dodatnim adresem. Aby zlokalizować punkty na tej linii, system kartezjański, który składa się z przypisania każdego punktu linii, jest używany liczba.

[TOC]

Formuła

Odległość euklidianowa d (a, b) jest zdefiniowana między punktami A i B, znajdującymi się na linii, takim jak pierwiastek kwadratowy kwadratu różnic jego współrzędnych x:

D (a, b) = √ ((xb - xa)^2)

Ta definicja gwarantuje, że: odległość między dwoma punktami jest zawsze dodatnią. I że odległość między A i B jest równa odległości między B i A.

Rycina 1 pokazuje jedną wymiarową przestrzeń euklidowską utworzoną przez linię (OX) i kilka punktów na tej linii. Każdy punkt ma współrzędną:

Punkt A ma współrzędne xa = 2.5, B współrzędna XB = 4 i punkt C współrzędna XC = -2.5

Może ci służyć: prawdopodobieństwo częstotliwości: koncepcja, jak jest obliczane i przykłady

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ (2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Odległość euklidian w dwóch wymiarach

Dwie -wymiarowa przestrzeń euklidowa to płaszczyzna. Punkty płaszczyzny euklidowskiej spełniają aksjomaty geometrii euklidów, na przykład:

- Na dwóch punktach mija pojedyncza linia. 

- Trzy punkty w samolocie tworzą trójkąt, którego wewnętrzne kąty zawsze dodają 180º.

- W trójkącie prostokąta kwadrat przeciwprostokątnej jest równy sumę kwadratów nóg.

W dwóch wymiarach punkt ma współrzędne x i y. 

Na przykład punkt P ma współrzędne (XP, YP) ​​i punkt, który koordynował (XQ, YQ).

Odległość euklidesowa między punktem P i Q jest zdefiniowana z następującym wzorem:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Należy zauważyć, że ten wzór jest równoważny twierdzeniu Pitagorasa, jak pokazano na rycinie 2.

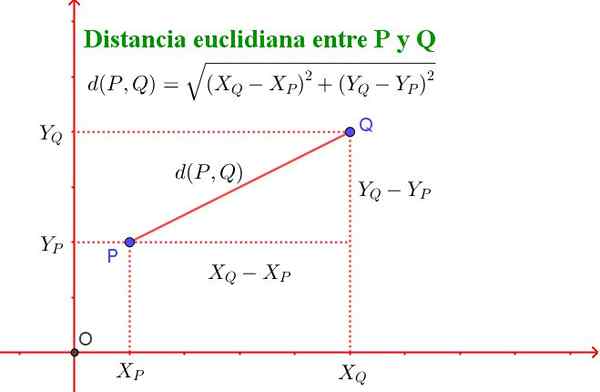Rysunek 2. Odległość między dwoma punktami P i Q samolotu spełnia twierdzenie Pitagorasa. (Przygotowane przez Ricardo Pérez).

Powierzchnie nieuklidyjskie

Nie wszystkie dwie -wymiarowe przestrzenie spełniają geometrię euklidesową. Powierzchnia kuli jest przestrzenią dwuwymiarową.

Kąty trójkąta na sferycznej powierzchni nie dodają 180º, a wraz z tym twierdzenie Pitagoras nie jest wypełnione, dlatego powierzchnia sferyczna nie spełnia aksjomatów euklidy.

Odległość euklidian w N Wymiarach

Pojęcie współrzędnych można rozszerzyć na większe wymiary:

- W punkcie 2-D ma współrzędne (XP, YP)

- W punkcie 3D, który ma współrzędne (XQ, YQ, ZQ)

- W punkcie 4-D będzie miał współrzędne (XR, YR, ZR, WR)

- W N-D punkt P będzie miał współrzędne (P1, P2, P3, ..., PN)

Może ci służyć: słupki Wykres: Charakterystyka, do czego jest przykłady

Odległość między dwoma punktami P i Q n-wymiarowej przestrzeni euklidowskiej jest obliczana z następującym wzorem:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +… +(qn - pn)^2)

Geometryczne miejsce wszystkich punktów, które w N-wymiarowej przestrzeni euklidesowej, które równoległe z innego ustalonego punktu P (środek) tworzy N-wymiarową hipersferę.

Jak obliczyć odległość euklidów

Poniżej znajduje się odległość między dwoma punktami znajdującymi się w euklidyjskiej przestrzeni trójwymiarowej.

Załóżmy punkt A współrzędnych kartezjańskich x, y, z podany przez A :( 2, 3, 1) i punkt B współrzędnych B :( -3, 2, 2).

Chcesz określić odległość między tymi punktami, dla których stosuje się ogólny związek:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5,196

Przykład

Istnieją dwa punkty P i Q.  Punkt P dla współrzędnych kartezjańskich x, y, z podany przez p :( 2, 3, 1) i punkt q współrzędnych q :( -3, 2, 1).

Poproszono o znalezienie współrzędnych punktu środkowego M segmentu [PQ], który łączy dwa punkty. 

Rozwiązanie:

Zakłada się, że nieznany punkt M ma współrzędne (x, y, z).

Ponieważ M jest średnim punktem [pq], należy spełnić, że d (p, m) = d (q, m), więc należy go również spełnić d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Podobnie jak w tym przypadku trzecia termin jest taki sam w dwóch członkach, poprzednie wyrażenie jest uproszczone do:

Może ci służyć: bezwzględna stała

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Istnieje wtedy równanie z dwoma niewiadomymi x i y. Do rozwiązania problemu wymagane jest inne równanie.

Punkt M należy do linii przechodzącej przez punkty P i Q, które możemy obliczyć w następujący sposób:

Pierwszy to wektor reżysera PQ linii: PQ = = .

Następnie PO POŁUDNIU = Op + Do PQ, Gdzie Op Jest to pozycja wektorowa punktu p i Do Jest to parametr należący do liczb rzeczywistych. 

Poprzednie równanie jest znane jako równanie wektorowe linii, które we współrzędnych kartezjańskich przyjmuje następująco:

= + a =

Równe odpowiednie komponenty to:

X - 2 = 2 - 5 a; I - 3 = 3 -A; Z - 1 = 0

To znaczy, że x = 4 - 5a, y = 6 - a, wreszcie z = 1.

Jest zastępowany w wyrażeniu kwadratowym, które odnosi się do x do y:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - a - 2)^2

Jest uproszczony:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Teraz rozwija się:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

Jest uproszczony, anulując podobne warunki w obu członkach:

4 - 20A + 9 - 6A = 49 - 70A + 16 - 8A

Parametr A:

52 A = 49 + 16 - 4 - 9 = 52 wynika, że ​​A = 1.

To znaczy, że x = 4 - 5, y = 6 - 1, wreszcie z = 1.

Wreszcie uzyskujemy kartezjańskie współrzędne punktu środkowego M segmentu [PQ]:

M: (-1, 5, 1).

Bibliografia

1. Lehmann c. (1972) Geometria analityczna. Uteha.
2. Superprof. Odległość między dwoma punktami. Odzyskane z: Superprof.Jest
3. Unam. Odległość między powiązanymi odmianami podliniowymi. Odzyskany z: Prometeusz.Matem.Unam.MX/
4. Wikipedia. Odległość euklidyjska. Odzyskane z: jest.Wikipedia.com
5. Wikipedia. Przestrzeń euklidesowa. Odzyskane z: jest.Wikipedia.com