Różnica między wspólną frakcją a liczbą dziesiętną

Do identyfikacji Jaka jest różnica między wspólną frakcją a liczbą dziesiętną Wystarczy obserwować oba elementy: jeden reprezentuje liczbę racjonalną, a drugi obejmuje w konstytucji całą część, a druga dziesiętna.

„Wspólna frakcja” jest wyrazem jednej ilości podzielonej między inną, bez uczynienia tego podziału. Matematycznie wspólna frakcja to liczba racjonalna, która jest zdefiniowana jako stosunek dwóch liczb całkowitych „A/B”, gdzie B ≠ 0.

„Liczba dziesiętna” to liczba składająca się z dwóch części: całej części i części dziesiętnej.

Aby oddzielić całą część części dziesiętnej, umieszcza się przecinek, zwany śpiączką dziesiętną, chociaż w zależności od bibliografii używany jest również punkt.

Liczby dziesiętne

Liczba dziesiętna może mieć skończoną lub nieskończoną liczbę liczb w swojej części dziesiętnej. Ponadto nieskończoną ilość dziesiętnych można podzielić na dwa typy:

Okresowy

To znaczy ma wzór powtórzeń. Na przykład 2 454545454545…

Nieodperiowy

Nie mają wzorca powtórzeń. Na przykład 1 7845265397219…

Liczby, które mają okresową ilość lub nieskończoną dziesiętne, nazywane są liczbą wymierną, podczas gdy ci, którzy mają nieskończoną ilość nieodprawną, nazywane są irracjonalnymi.

Związek zbioru liczb wymiernych i zestaw liczby irracjonalnych jest znany jako zbiór liczb rzeczywistych.

Różnice między wspólną frakcją a liczbą dziesiętną

Różnice między wspólną frakcją a liczbą dziesiętną to:

1- Część dziesiętna

Każda wspólna frakcja ma skończoną liczbę liczb w części dziesiętnej lub okresową nieskończoną ilość, podczas gdy liczba dziesiętna może mieć nieskończoną liczbę liczb w swojej części dziesiętnej.

Powyższe mówi, że każda liczba racjonalna (każda wspólna frakcja) jest liczbą dziesiętną, ale nie każda liczba dziesiętna jest liczbą racjonalną (wspólna frakcja).

2- Notacja

Każda wspólna frakcja jest oznaczona jako stosunek dwóch liczb całkowitych, podczas gdy irracjonalnej liczby dziesiętnej nie można w ten sposób oznaczyć.

Najczęściej używane irracjonalne liczby dziesiętne w matematyce są oznaczone korzeniami kwadratowymi (√ ), sześcienne (³√ ) i wyższe stopnie.

Oprócz nich istnieją dwie bardzo znane liczby, które są liczbą Eulera, oznaczonej przez E; I numer PI, oznaczony przez π.

Jak przejść od wspólnej ułamka do liczby dziesiętnej?

Aby przejść ze wspólnej frakcji do liczby dziesiętnej, wystarczy tylko dla odpowiedniego podziału. Na przykład, jeśli masz 3/4, odpowiednia liczba dziesiętna wynosi 0,75.

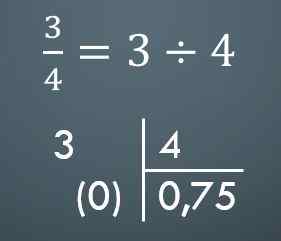
Jak przejść od racjonalnej liczby dziesiętnej do wspólnej frakcji?

Można również przeprowadzić odwrotny proces do poprzedniego. Poniższy przykład ilustruje technikę przejścia od racjonalnej liczby dziesiętnej do wspólnej frakcji:

- Niech x = 1,78

Ponieważ x ma dwa dziesiętne, wówczas poprzednia równość jest mnożona przez 10² = 100, co uzyskuje 100x = 178; I wyczyszczenie x okazuje się, że x = 178/1. To ostatnie wyrażenie jest wspólną frakcją reprezentującą liczbę 1.78.

Ale czy ten proces można wykonać dla liczb z okresową nieskończoną ilością dziesiętnych? Odpowiedź brzmi „tak”, a poniższy przykład pokazuje kroki do śledzenia:

- Niech x = 2.193193193193 ..

Ponieważ okres tej liczby dziesiętnej ma 3 cyfry (193), poprzednie wyrażenie jest mnożone przez 10³ = 1000, co uzyskuje wyrażenie 1000x = 2193,193193193193… .

Ostatnie wyrażenie jest teraz odejmowane za pomocą pierwszej, a cała część dziesiętna jest anulowana, pozostawiając wyrażenie 999x = 2191, gdzie uzyskuje się, że wspólna frakcja wynosi x = 2191/999.