Różnica formuł, równania, przykładów, ćwiczeń

Różnica kostek Jest to dwumianowa algebraiczna ekspresja formy³ - B³, gdzie terminy A i B mogą być liczbami rzeczywistymi lub wyrażenia algebraiczne różnych typów. Przykładem różnicy kostek jest: 8 - x³, Ponieważ 8 można zapisać jako 2³.

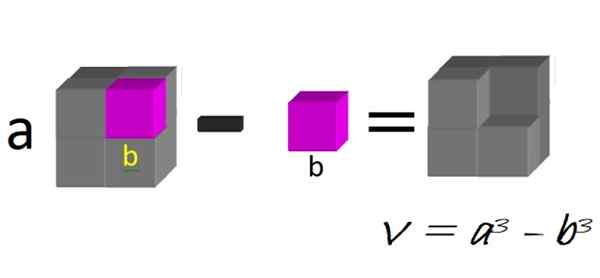
Geometrycznie możemy wymyślić dużą kostkę z boku A, do którego odejmuje się mały bube z boku B, jak pokazano na rycinie 1:

Rysunek 1. Różnica kostek. Źródło: f. Zapata.

Objętość uzyskanej liczby jest dokładnie różnicą w kostkach:

V = a³ - B³

Aby znaleźć alternatywne wyrażenie, zaobserwowano, że liczbę tę można podzielić na trzy pryzmaty, jak pokazano poniżej:

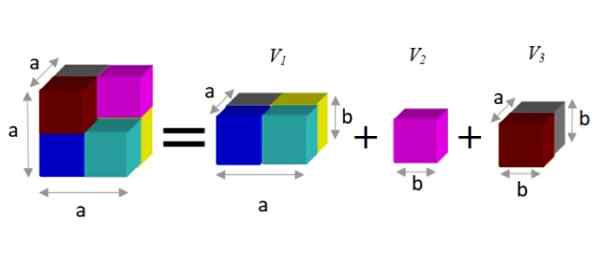Rysunek 2. Różnica w kostkach (po lewej równości) jest równa sumie objętości częściowych (po prawej). Źródło: f. Zapata.

Prism ma objętość podaną przez iloczyn trzech wymiarów: szerokość x wysoka x głębokość. W ten sposób wynikowy objętość to:

V = a³ - B³ = a².B + b³ + Do.B²

Czynnik B Jest to powszechne po prawej stronie. Ponadto na powyższym rysunku jest to spełnione, w szczególności::

B = (A/2) ⇒ A = B + B

Dlatego można powiedzieć, że: B = a - b. Zatem:

Do³ - B³ = B (a² + B² +Do.b) = (a-b) (a² + Do.B + b²)

Ten sposób wyrażania różnicy w kostkach okaże się bardzo przydatny w wielu aplikacjach i zostałby uzyskany w ten sam sposób, chociaż brakujący strona kostki w rogu różniła się od B = A/2.

Zauważ, że drugi nawiasDużo wygląda na niezwykły produkt kwadratu sum. Czytelnik może opracować prawą stronę, aby sprawdzić, czy jest skutecznie uzyskiwana Do³ - B³.

[TOC]

Może ci służyć: kwadratowy dwumian

Przykłady

Istnieje kilka różnic kostek:

1 - m⁶

Do⁶B³ - 8z¹²I⁶

(1/125).X⁶ - 27.I⁹

Analizujmy każdego z nich. W pierwszym przykładzie 1 można zapisać jako 1 = 1³ i termin m⁶ Pozostaje: (m²)³. Oba terminy są doskonałymi kostkami, dlatego ich różnica polega na:

1 -m⁶ = 1³ - (M²)³

W drugim przykładzie terminy są przepisywane:

Do⁶B³ = (a²B)³

8z¹²I⁶ = 2³ (z⁴)³ (I²)³ = (2Z⁴I²)³

Różnica tych kostek to: (²B)³ - (2Z⁴I²)³.

Wreszcie frakcja (1/125) wynosi (1/5³), X⁶ = (x²)³, 27 = 3³ i i⁹ = (i³)³. Zastępując to wszystko w oryginalnym wyrażeniu, jest uzyskiwane:

(1/125).X⁶  - 27Y⁹ = [(1/5) (x²)]³ - (3y³)³

Różnica kostki

Fakt różnica w kostkach upraszcza wiele operacji algebraicznych. Aby to zrobić, wystarczy użyć wcześniej odliczonej formuły:

Rysunek 3. Czynnik różnicy w kostkach i ekspresja niezwykłego ilorazu. Źródło: f. Zapata.

Teraz procedura zastosowania tej formuły składa się z trzech kroków:

- Po pierwsze, uzyskuje się korzeń sześcienny każdego z terminów różnicy.

- Następnie budowane są dwumianowe i trynomialne, które pojawiają się po prawej stronie formuły.

- Wreszcie dwumianowy i trynomiczny jest zastępowany w celu uzyskania końcowej czynników.

Zilustrujemy zastosowanie tych kroków z każdym z przykładów różnicy kostek zaproponowanych powyżej, a tym samym uzyskuje jego faktoryzowany równoważny.

Przykład 1

Wyrażenie faktyczne 1 -m⁶   Po opisanych krokach. Zaczynamy od przepisania wyrażenia jako 1 -m⁶ = 1³ - (M²)³ Wyodrębnić odpowiednie korzenie sześcienne każdego terminu:

Następnie buduje się dwumianowy i trójmian:

Może ci służyć: teoria kolejki: historia, model, do czego służy i przykłady

A = 1

B = m²

Więc:

A - b = 1 - m²

 (Do² +Do.B + b²) = 1² + 1.M² + (M²)² = 1 + m² + M⁴

 Wreszcie jest zastąpiony w Formule A³ - B³ = (a-b) (a² +Do.B + b²):

1 -m⁶ = (1 - m²) (1 + m² + M⁴)

Przykład 2

Rozkładać na czynniki:

Do⁶B³ -8z¹²I⁶ = (a²B)³ - (2Z⁴I²)³

Ponieważ są to idealne kostki, korzenie sześcienne są natychmiastowe: a²B i 2Z⁴I², Stamtąd następuje:

- Binomial: a²B - 2Z⁴I²

- Trinomial: (a²B)² + Do²B. 2Z⁴I² + (Do²B +2Z⁴I²)²

 A teraz zbudowana jest pożądana czynnik:

Do⁶B³ -8z¹²I⁶ = (a²B - 2Z⁴I²). [(Do²B)² + Do²B. 2Z⁴I² + (Do²B + 2Z⁴I²)²] =

= (a²B - 2Z⁴I²). [Do⁴B² + 2²B.z⁴I² + (Do²B + 2Z⁴I²)²]

Zasadniczo faktoralizacja jest gotowa, ale często konieczne jest uproszczenie każdego terminu. Następnie niezwykły produkt jest opracowywany z sumy - który pojawia się na końcu, a następnie dodaje podobne warunki. Pamiętając, że kwadrat sumie to:

(x + y)² = x² + 2xy + i²

W ten sposób staje się godne uwagi prawo do prawej:

(Do²B + 2Z⁴I²)² = a⁴B² + 4²B.z⁴I² + 4Z⁸I⁴

 Zastąpienie rozwoju uzyskanego w faktoryzacji różnicy w kostkach:

Do⁶B³ -8z¹²I⁶ = (a²B - 2Z⁴I²). [Do⁴B² + 2²B.z⁴I² + Do⁴B² + 4²B.z⁴I² + 4Z⁸I⁴] =

Wreszcie, grupowanie podobnych terminów i uwzględnianie współczynników numerycznych, które są parami, uzyskuje się:

(Do²B - 2Z⁴I²). [2⁴B² + 6th²B.z⁴I² + 4Z⁸I⁴] = 2 (a²B - 2Z⁴I²). [Do⁴B² + 3²B.z⁴I² + 2Z⁸I⁴]

Przykład 3

Factorize (1/125).X⁶  - 27Y⁹ Jest znacznie prostszy niż poprzedni przypadek. Najpierw zidentyfikowane są odpowiedniki A i B:

A = (1/5) x²

B = 3y³

Następnie są zastępowane bezpośrednio w formule:

(1/125).X⁶  - 27Y⁹ = [(1/5) x² - 3y³]. [(1/25) x⁴ + (3/5) x²I³ + 9Y⁶]

Ćwiczenie rozwiązane

Różnica w kostkach ma, jak powiedzieliśmy, różnorodne zastosowania w algebrze. Spójrzmy na niektóre:

Może ci służyć: 5 cech płaszczyzny kartezjańskiej

Ćwiczenie 1

Rozwiąż następujące równania:

a) x⁵ - 125 x² = 0

b) 64 - 729 x³ = 0

Rozwiązanie

Najpierw równanie jest czynnikiem w ten sposób:

X² (X³ - 125) = 0

Ponieważ 125 jest idealną kostką, nawias jest napisany jako różnica w kostkach:

X² . (X³ - 5³) = 0

Pierwsze rozwiązanie to x = 0, ale znajdujemy więcej, jeśli zrobimy x³ - 5³ = 0, zatem:

X³ = 5³ → x = 5

Rozwiązanie b

Lewa strona równania jest przepisana jako 64 - 729 x³ = 4³ - (9x)³. Dlatego:

4³ - (9x)³ = 0

Ponieważ wykładnik jest taki sam:

9x = 4 → x = 9/4

Ćwiczenie 2

Express Freacate:

(x + y)³ - (X - y)³

Rozwiązanie

To wyrażenie jest różnicą w kostkach, jeśli w formule faktoryzacji zauważamy, że:

A = x+ i

b = x- y

Następnie najpierw budowany jest dwumianowy:

a - b = x+ y - (x- y) = 2y

A teraz trójmian:

Do² + Do.B + b² = (x+ y)² + (x + y) (x-y) + (x-y)²

Opracowywane są godne uwagi produkty:

(x+ y)² = x² + 2xy +i²

(x+y) (x-y) = x²- I²

(X-y)² = x² - 2xy +i²

Następnie musisz wymienić i zmniejszyć podobne warunki:

Do² + Do.B + b² = x² + 2xy +i²+ X²- I²+ X² - 2xy +i² = 3x² + I²

Faktoralizacja powoduje:

(x + y)³ - (X - y)³ = 2y. (3x² + I²)

Bibliografia

1. Baldor, a. 1974. Algebra. Wenezuelskie redakcje kulturalne.DO.
2. Fundacja CK-12. Suma i różnica kostek. Odzyskane z: CK12.org.
3. Khan academy. KOGROWANIA Różnica w kostkach. Odzyskane z: jest.Khan academy.org.
4. Matematyka jest zabawna zaawansowana. Różnica dwóch kostek. Odzyskany z: MathSisfun.com
5. Unam. Różnica kostki. Źródło: DCB.Fi-c.Unam.MX.