Przemieszczenie kątowe

Co to jest przemieszczenie kątowe?

On Przemieszczenie kątowe Jest to zmiana lub zmienność pozycji kątowej, którą obiekt w doświadczeniach rotacji, zwykle mierzony w radianach lub w jakiejkolwiek innej miarie podanej dla zakrętów, takich jak oceny lub rewolucje.

Gdy obiekt obraca się wokół stałej osi, jego przemieszczenie kątowe jest określane przez pomiar kąta zmiecionego przez linię, która przechodzi przez dowolny punkt ciała, przecinając oś obrotu, to znaczy linii promieniowej.

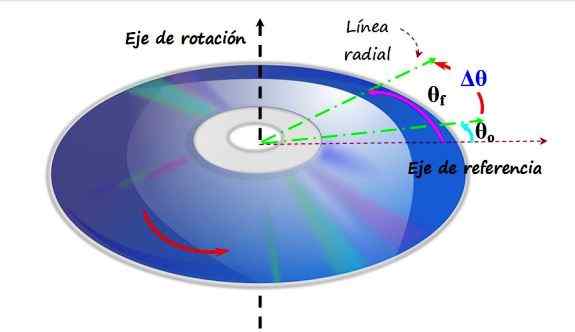Compact Disc lub Cd obraca się w kierunku przeciwhoranantowym wokół pionowej osi obrotu. Przechodząc od kąta θo do θf, mówi się, że doświadczył przemieszczenia kątowego. Źródło: f. Zapata.

Na górnej figurze znajduje się CD, która obraca się w kierunku antyhorarycznym, będąc oś obrotu osi pionowy. Oś odniesienia jest umieszczana na płaszczyźnie CD, która odpowiada kąta 0 radianom lub 0. Zielona linia to linia promieniowa, która początkowo tworzy kąt θ_albo Z odniesieniem. To jest twoja początkowa pozycja.

Później zielona linia przesuwa się do nowej pozycji o nazwie θ_F, A doświadczenie doświadczone, zwane δθ jest po prostu:

Δθ = θ_F - θ_albo

Każdy punkt P CD doświadcza tego samego przemieszczenia kątowego w określonym przedziale czasowym, z wyjątkiem środka, w którym przechodzi oś obrotu.

Wzory i równania

Istnieje obiekt, który obraca się wokół stałej osi lub pozostawia ekran do czytelnika. I w nim znajduje się punkt P, znajdujący się w odległości r osi obrotu i opisujący obwody radiowe R.

Jest to widoczne na poniższym rysunku, który pokazuje obiekt cięcia, widać wbrew igieł zegarowy. Punktem, o którym mowa, znajduje się w pozycji kątowej θ, mierzona od osi odniesienia, która w tym przypadku jest oś pozioma.

Może ci służyć: zasada addytywna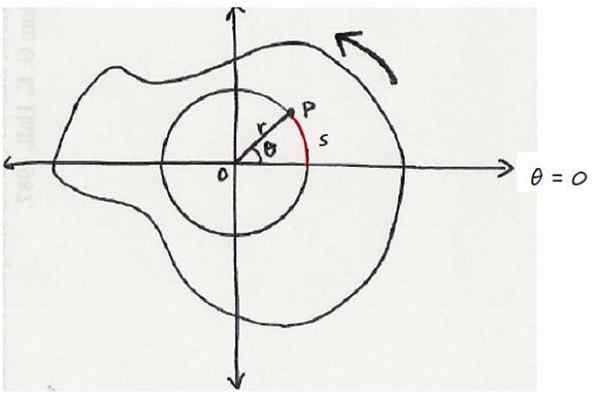Obiekt, który obraca się w sensie antyhorarycznym. Oś obrotu wychodzi prostopadle do ekranu. Źródło: Wikimedia Commons.

Zgodnie z konwencją, do rotacji w sensie przeciwhorarycznym, ma przypisany sens pozytywny, podczas gdy rotacja w harmonogramie ma znak ujemny.

Gdy punkt przekształca kąt θ, jednocześnie przemierza łuk. Ponieważ θ jest kątem centralnym, ponieważ jego wierzchołek zajmuje środek obwodu, spełnia się, że:

Z θ wyrażonym w radiach.

Przemieszczenie kątowe to:

Δθ = θ_finał  - θ_wstępny

Na przykład, jeśli p zaczął się od θ_wstępny = 0 rad, a następnie jest w θ_finał = 0.8 rad, jego przemieszczenie kątowe pochodzi z:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Inne punkty obiektu mogą zajmować różne pozycje kątowe, ale wszystkie doświadczają tego samego przemieszczenia kątowego. Jednak najbardziej odległe cząstki z centrum przejeżdżają większe odległości, ponieważ s = r⋅θ.

Kąty mierzą

W rotacji często znajdują kąty mierzone w radianach, ale występują również w stopniach i rewolucjach lub zakrętach. W rozwiązywaniu problemów konieczne jest przejście od tych jednostek do radian.

1 Rewolucja jest równoważna kompletnego zakrętu, to znaczy, gdy całkowitą zwrot zerwała, zmieniła 360 ° i są one równoważne z 2π radianami, ponieważ w tym przypadku punkt zwiedził łuk równy 2πr:

Ale upraszczając, poprzednią równoważność można wyrazić w następujący sposób:

π radian = 180º

Jak obliczane jest przemieszczenie kątowe?

Przemieszczenie kątowe można obliczyć analogicznie na sposób, w jaki przemieszczenie w ruchu jest obliczane w wymiarze, zgodnie z pewnym modelem ruchu. W tym celu średnia prędkość kątowa definiuje się jako przemieszczenie kątowe δθ w danym przedziale czasowym ΔT:

Gdzie średnia prędkość kątowa jest oznaczona jako ω_M i jest podawany w radianach w jednostkach systemu międzynarodowego, jeśli.

Może ci służyć: jak uzyskać kąt trójkąta? (Przykład)

Natychmiastowa prędkość kątowa jest granicą średniej prędkości kątowej, gdy δT → 0:

Oznacza to, że jest to pierwsze pochodzące z pozycji kątowej w odniesieniu do czasu. Z kolei można zdefiniować przyspieszenie kątowe, oznaczone jako α, co jest równoważne z pochodną lub szybkością zmiany prędkości kątowej w odniesieniu do czasu:

Które można również interpretować jako drugi pochodzący z pozycji kątowej w odniesieniu do czasu.

Ważne jest to, że dwa modele ruchu można ustalić w analogicznych ruchach prostoliniowych, ponieważ chociaż obroty są przeprowadzane w płaszczyźnie, pojedyncza współrzędna kątowa jest wystarczająca do ustalenia położenia dowolnego punktu obiektu.

Jednolity ruch kołowy

W jednolitym ruchu okrągłym prędkość kątowa jest stała, to znaczy średnia prędkość kątowa jest równa natychmiastowej prędkości kątowej. Ponieważ przyspieszenie kątowe α jest równe 0, możesz napisać następujące równanie dla pozycji jako funkcji czasu:

θ = θ_albo + ωt

Gdzie θ_albo Jest to początkowa pozycja telefonu komórkowego.

Równomiernie przyspieszony ruch kołowy

W tym przypadku przyspieszenie kątowe α jest stałe i w analogice z równomiernie zróżnicowanym ruchem prostoliniowym można zapisać następujące równania:

• θ = θ_albo + Ω_albo T + ½ αT²
• Ω = ω_albo + αT 
• Ω² = Ω_albo² + 2α ∙ θθ

Ćwiczenie rozwiązane

Pierwsze ćwiczenie

Można założyć, że Ziemia jest sztywnym obiektem, który obraca się na stałej osi i że jej obrót jest prawie jednolity. W przedziale czasowym ΔT = 12 godzin Znajdź:

a) Przemieszczenie kątowe Ziemi

b) Twoja prędkość kątowa

c) przyspieszenie kątowe w tym przedziale czasowym.

Rozwiązanie

Wiedząc, że za 24 godziny Ziemia całkowicie obraca się wokół osi, za 12 godzin obrócisz połowę okrążenia, to znaczy π radian. Jeśli jest uważane za część θ_wstępny = 0 rad, jego przemieszczenie kątowe wynosi:

Może ci służyć: Zasada multiplikatywna: Techniki zliczania i przykłady

Δθ = π radian

Rozwiązanie b

Ponieważ obrót jest jednolity, prędkość kątowa jest ilorazem między przesunięciem kątowym a czasem, ponadto 1 godzinę = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 rad/s.

Rozwiązanie c

Przyspieszenie kątowe jest nieważne, ponieważ obrót ziemi jest jednolity.

Drugie ćwiczenie

Juan przebiegł odległość 35 metrów na okrągłym torze lekkoatletycznym, którego promień jest równy 7 metrów. Oblicz przemieszczenie kątowe, które dokonał Juan.

Rozwiązanie

Ponieważ odległość przejechanego łuku i promień obwodu jest znany, drugą formułę można zastosować, aby poznać przesunięcie kątowe wykonane przez Juana. Korzystając z opisanego powyżej wzoru, musisz θ = 35/7 = 5 radian.

Trzecie ćwiczenie

Jeśli Mario musi w swoim pojeździe, połowa okrągłego toru wyścigowego, jakie jest przemieszczenie kątowe, które zrobił Mario?

Rozwiązanie

W tym ćwiczeniu obowiązuje pierwsza formuła. Ponieważ wiadomo, że Mario przejechał połowę toru, można założyć, że rozpoczął wyścig pod kątem 0 °. Dlatego odpowiedź to 180 ° -0 ° = 180 ° = π radian.

Czwarte ćwiczenie

Maria ma okrągły basen. Twój pies biegnie wokół basenu, jeżdżąc w odległości 18 metrów. Jeśli promień basenu wynosi 3 metry, jakie jest przesunięcie kątowe wykonane przez zwierzaka Marii?

Rozwiązanie

Ponieważ basen jest okrągły, a jego promień jest znany, możesz przystąpić do użycia drugiej formuły.

Wiadomo, że promień jest równy 3 metrów, a odległość przebywająca przez zwierzaka jest równa 18 metrów. Dlatego wykonane przesunięcie kątowe jest równe θ = 18/3 = 6 radian.

Bibliografia

1. Katz, d. 2013. Fizyka dla naukowców i inżynierów. Fundamenty i połączenia. Cengage Learning.
2. Rex, a. 2011. Podstawy fizyki. osoba.
3. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1. osoba.
4. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.
5. Tipler, str. (2006). Fizyka nauk i technologii. Ed. Tom 1. Redakcja Reverted.