Nierówność trójkąta demonstracyjnego, przykłady, ćwiczenia rozwiązane

Nazywa się Nierówność trójkąta do właściwości, która spełnia dwie liczby rzeczywistych składające się z wartości bezwzględnej jej sumy, jest zawsze mniejsza lub równa sumie jej wartości bezwzględnych. Ta właściwość jest również znana jako nierówność Minkowski lub nierówność trójkątna.

Ta właściwość liczb nazywa się nierównością trójkątną, ponieważ w trójkątach zdarza się, że długość jednej strony jest zawsze mniejsza lub równa sumie pozostałych dwóch, nawet jeśli ta nierówność nie zawsze ma zastosowanie w dziedzinie trójkątów.

Rysunek 1. Wartość bezwzględna sumy dwóch liczb jest zawsze mniejsza lub równa sumie jej wartości bezwzględnych. (Przygotowane przez R. Pérez)

Istnieje kilka demonstracji trójkątnej nierówności w liczbach rzeczywistych, ale w tym przypadku wybierzemy na podstawie właściwości wartości bezwzględnej i kwadratowej dwumianowej.

Twierdzenie: Dla wszystkich pary liczb Do I B Należąc do liczb rzeczywistych, musi:

|. A + B | ≤ | A | + | B |

[TOC]

Demonstracja

Zaczynamy od rozważenia pierwszego członka nierówności, który zostanie odcięty:

|. A + b |^2 = (a + b)^2 = a^2 + 2 a b + b^2 (ec. 1)

W poprzednim kroku nieruchomość została użyta, że ​​dowolna liczba wysoki do kwadratu jest równa wartości bezwzględnej wspomnianej liczby wysokiej do kwadratu, to znaczy: | x |^2 = x^2. Zastosowano również rozwój kwadratowego dwumianowego.

Cała liczba X Jest mniejszy lub równy swojej wartości bezwzględnej. Jeśli liczba jest dodatnia, jest warta równości, ale jeśli liczba jest ujemna, zawsze będzie mniejsza niż liczba dodatnia. W tym przypadku jego własna wartość bezwzględna, to znaczy, że można to powiedzieć x ≤ | x |.

Może ci służyć: programowanie nieliniowe: metody i ćwiczenia

Produkt (A B) Jest to liczba, dlatego jest to stosowane (a b) ≤ | A B |. Po zastosowaniu tej właściwości (WE. 1) Mamy:

|. A + B |^2 = A^2 + 2 (A B) + B^2 ≤ A^2 + 2 | A B | + B^2 (WE. 2)

Biorąc to pod uwagę |. A B | = | A || B | LA (WE. 2) Można go zapisać w następujący sposób:

 |. A + B |^2 ≤ A^2 + 2 | A || B | + B^2 (WE. 3)

Ale jak powiedzieliśmy wcześniej, że kwadrat liczby jest równy wartości bezwzględnej liczby wysokiej do kwadratu, wówczas równanie 3 można przepisać w następujący sposób:

 |. A + B |^2 ≤ | a |^2 + 2 | a | | B | + | B |^2 (WE. 4)

W drugim członku nierówności uznaje się niezwykły produkt, który po zastosowaniu prowadzi do:

 |. A + B |^2 ≤ (| A | + | B |)^2 (EC. 5)

W poprzednim wyrażeniu należy zauważyć, że wartości, które należy podnieść na obu członkach nierówności, są również pozytywne, że należy go również spełnić:

 |. A + B | ≤ (| a |+ | b |) (ec. 6)

Poprzednie wyrażenie jest dokładnie tym, co chciałeś zademonstrować.

Przykłady

Następnie sprawdzimy trójkątną nierówność z kilkoma przykładami.

Przykład 1

Wartość jest pobierana a = 2, a wartość b = 5, to znaczy zarówno liczb dodatnich, jak i zweryfikujemy, czy nierówność jest spełniona.

 |. 2 + 5 | ≤ | 2 |+ | 5 |

 |. 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

Równość jest weryfikowana, dlatego twierdzenie o nierównościach trójkąta zostało spełnione.

Przykład 2

Wybierane są następujące wartości a = 2 i b = -5, to znaczy liczba dodatnia, a druga negatywna, sprawdzamy, czy nierówność jest spełniona.

Może ci służyć: trójmian

 |. 2 - 5 | ≤ | 2 |+ | -5 |

 |. -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

Nierówność jest wypełniona, dlatego trójkątne twierdzenie o nierównościach zostało zweryfikowane.

Przykład 3

Wartość jest pobierana a = -2, a wartość b = 5, to znaczy liczba ujemna, a druga dodatnia, weryfikujemy, czy nierówność jest spełniona.

 |. -2 + 5 | ≤ | -2 |+ | 5 |

 |. 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

Nierówność jest weryfikowana, dlatego twierdzenie zostało spełnione.

Przykład 4

Wybierane są następujące wartości a = -2 i b = -5, to znaczy zarówno liczby ujemne, jak i sprawdzamy, czy nierówność jest spełniona.

 |. -2 - 5 | ≤ | -2 |+ | -5 |

 |. -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

Równość jest weryfikowana, dlatego twierdzenie o nierówności Minkowsk zostało spełnione.

Przykład 5

Wartość jest pobierana a = 0, a wartość b = 5, to znaczy liczba zerowa i druga dodatnia, a następnie sprawdzamy, czy nierówność jest spełniona.

 |. 0 + 5 | ≤ | 0 |+ | 5 |

 |. 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

Równość jest spełniona, dlatego twierdzenie o nierównościach trójkąta zostało zweryfikowane.

Przykład 6

Wartość jest pobierana a = 0, a wartość b = -7, to znaczy stwierdzenie liczby zerowej i drugiej pozytywnej, a następnie sprawdzamy, czy nierówność jest spełniona.

 |. 0 - 7 | ≤ | 0 |+ | -7 |

 |. -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

Równość jest weryfikowana, dlatego trójkątna twierdzenie o nierównościach zostało spełnione.

Rozwiązane ćwiczenia

W poniższych ćwiczeniach geometrycznie reprezentuje nierówność trójkąta lub nierówność Minkowskiego dla liczb A i B.

Może ci służyć: papomudas

Liczba A będzie reprezentowana jako segment na osi x, jego pochodzenie lub pokrywa się z zerową osą x i drugim końcem segmentu (w punkcie P) będzie w kierunku dodatnim (po prawej) x osi, jeśli a> 0, ale do < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Podobnie liczba B będzie reprezentowana jako segment, którego pochodzenie jest na punkcie P. Drugi koniec, to znaczy punkt, który będzie po prawej stronie p, jeśli b jest dodatni (b> 0), a punkt q będzie | b | Jednostki po lewej stronie p if b<0.

Ćwiczenie 1

Graficznie reprezentuje nierówność trójkąta dla A = 5 i B = 3 |. A + B | ≤ | A | + | B |, istnienie C = A + B. 

Rozwiązanie 1: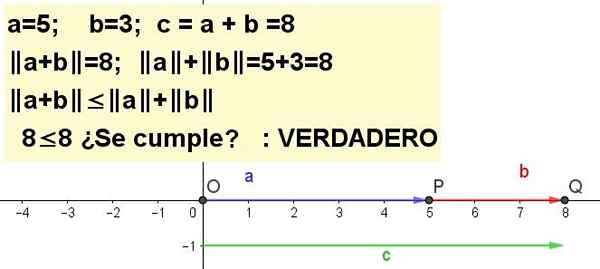

Ćwiczenie 2

Wykonaj trójkątny wykres nierówności dla A = 5 i B = -3. 

|. A + B | ≤ | A | + | B |, istnienie C = A + B.

Rozwiązanie 2:

Ćwiczenie 3

Wykres nierówność trójkąta dla A = -5 i B = 3.

|. A + B | ≤ | A | + | B |, istnienie C = A + B. 

Rozwiązanie 3: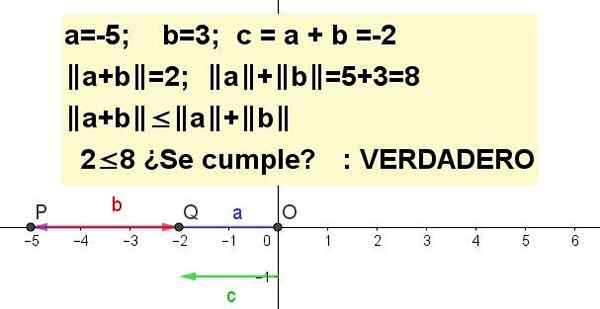

Ćwiczenie 4

Wykres trójkątnej nierówności dla A = -5 i B = -3.

|. A + B | ≤ | A | + | B |, istnienie C = A + B.

Rozwiązanie 4: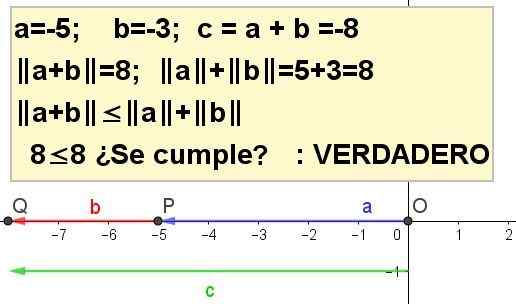

Bibliografia

1. I. Whitesitt. (1980).Boolean Algebra i jej zastosowania . Continental Redaktorial Company C. DO.
2. Mícheal lub „searcoid.(2003) Elementy analizy abstrakcyjnej ... Departament Matematyki. University College Dublin, Beldfield, Dubllind.
3. J. Van Wyk. (2006) Matematyka i inżynieria w informatyce. Instytut Nauk Komputerowych i technologii. Krajowe Biuro Standardów. Waszyngton, zm. C. 20234
4. Eric Lehman. Matematyka informatyki.  Google Inc.
5. F Thomson Leighton (1980). Rachunek różniczkowy. Department of Mathematics and the Computer Science and AI Laboratory, Massachussetts Institute of Technology.
6. Khan academy. Twierdzenie o nierównościach trójkąta. Odzyskane z: Khanacademy.org
7. Wikipedia. Trójkątna nierówność. Odzyskane z: jest. Wikipedia.com